Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek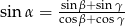 
to trójkąt ten jest prostokątny.
/Konkursy
Na bokach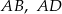 
i 
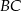rombu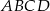 
wybrano odpowiednio punkty 
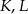i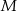 
w ten sposób, że odcink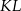i 
i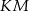 
są równoległe do przekątnych rombu. Wykaż, że odcinek 
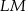przechodzi przez punkt przecięcia przekątnych rombu.
Pudełko czekoladek kosztuje 10 zł. W każdym pudełku znajduje się kupon. Za każde trzy kupony możemy otrzymać dodatkowe pudełko czekoladek gratis. Jaka jest największa liczba pudełek czekoladek, które możemy otrzymać za 150 zł.?
A) 15 B) 17 C) 20 D) 21 E) 22
Prostokąt na rysunku tworzy sześć kwadratów. Długość boku najmniejszego kwadratu jest równa 1. Jaką długość ma bok największego kwadratu.
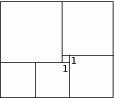
A) 4 B) 5 C) 6 D) 7 E) 8
Długości podstaw trapezu równoramiennego są równe 
oraz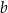 
, przy czym 
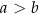. W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od 
.
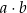Dla każdej liczby rzeczywistej 
oznaczamy przez 
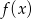najmniejszą z liczb 
, 
, 
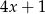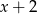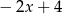. Największą wartością 
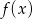jest liczba
A) 1/2 B) 2/3 C) 7/3 D) 8/3 E) 3
Wyznacz wszystkie liczby naturalne dodatnie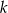 
, dla których równanie 
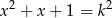ma pierwiastki będące liczbami całkowitymi.
Wykaż, że liczba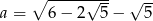 
jest całkowita.
Ukryj
Podobne zadania
Wykaż, że liczba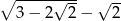 
jest liczbą całkowitą.
Wykaż, że liczba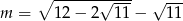 
jest wymierna.
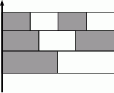
Flagę tworzą trzy pasy jednakowej szerokości podzielone odpowiednio na dwie, trzy i cztery równe części (rysunek obok). Jaką część flagi zacieniowano?
A)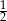 
B) 
C) 
D) 
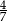E)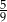 
W trapez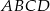 
, gdzie 
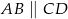i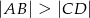 
, wpisano okrąg (patrz rysunek).
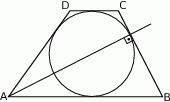
Dwusieczna kąta ostrego przy wierzchołku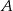 
jest prostopadła do ramienia 
.
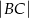- Wykaż, że dwusieczna kąta przy wierzchołku
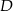jest równoległa do ramienia 
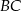. - Oblicz
.
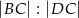Półkola na rysunku mają promienie równe 1. Ile jest równe pole zacieniowanego obszaru?
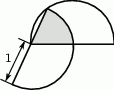
A)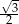 
B) 
C) 
D) 
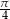E)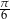 
Grupa szachistów postanowiła zorganizować turniej szachowy w systemie każdy z każdym. Rozgrywano 5 partii dziennie. Turniej trwał 9 dni. Ilu szachistów brało w nim udział ?
Zegarek babci Jasia spieszy się o jedną minutę w ciągu godziny, a zegarek jego dziadka spóźnia się o jedną minutę w ciągu godziny. Wychodząc po wizycie z domu babci i dziadka, Jasio ustawił na ich zegarkach ten sam czas i powiedział, że odwiedzi ich ponownie, gdy różnica czasu na ich zegarkach będzie wynosiła dokładnie jedną godzinę. Po ilu godzinach Jasio ponownie odwiedzi babcię i dziadka?
A) 12h B) 14h 30min C) 30h D) 60h E) 90h
Znajdź liczbę doskonałą, która jest podzielna przez 4 i ma dokładnie 6 dzielników.
Ile jest możliwych dróg o minimalnej liczbie ruchów, prowadzących z lewego górnego rogu diagramu do jego prawego dolnego rogu, które może wykonać król szachowy (w jednym ruchu król może przesunąć się na dowolne sąsiednie pole stykające się bokiem lub wierzchołkiem)?
A) 1 B) 4 C) 3 D) 20 E) 2
Gdyby Aleksander Wielki umarł o 5 lat wcześniej, to panowałby przez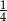 
swego życia. Gdyby żył o 9 lat dłużej, to panowałby przez połowę swego życia. Ile lat żył i ile lat panował.
Podstawy trapezu mają długości 10 i 6. Wiedząc, że suma miar kątów wewnętrznych przy dłuższej podstawie jest równa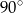 
, oblicz długość odcinka łączącego środki podstaw trapezu.
Podstawy trapezu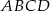 
mają długośc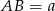i 
i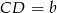 
. Na ramionach trapezu wybrano punkty 
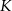i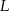 
w ten sposób, że odcinek 
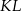jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka 
.
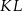W pewnej wiosce żadnych dwóch mieszkańców nie ma tej samej liczby włosów na głowie. Żaden z mieszkańców nie ma dokładnie 2007 włosów. Mieszkańcem tej wsi o największej liczbie włosów jest Kargul. Liczba mieszkańców jest większa od liczby włosów na głowie Kargula. W tej wiosce mieszka co najwyżej
A) 0 mieszkańców
B) 2006 mieszkańców
C) 2007 mieszkańców
D) 2008 mieszkańców
E) 2009 mieszkańców
W działaniu zamieszczonym obok każda litera oznacza pewną cyfrę, przy czym różne litery oznaczają różne cyfry. Jaka cyfra kryje się pod literą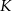 
?
A) 0 B) 1 C) 2 D) 8 E) 9
