W roku 2008 cyfra jedności jest czterokrotnością cyfry tysięcy. Jaka jest minimalna liczba lat, które muszą upłynąć, by taka sytuacja się powtórzyła?
A) 10 B) 20 C) 100 D) 2008 E) Inna odpowiedź
/Konkursy
Wysokość 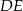 rombu
rombu 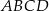 dzieli bok
dzieli bok 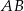 tego rombu tak, że
tego rombu tak, że 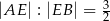 (zobacz rysunek).
(zobacz rysunek).
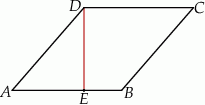
Oblicz wartość wyrażenia
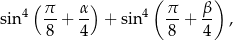
gdzie  i
i 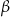 są dwoma sąsiednimi kątami wewnętrznymi rombu
są dwoma sąsiednimi kątami wewnętrznymi rombu 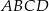 .
.
Uderzona silnie bila odbiła się od bandy stołu bilardowego pod kątem 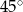 (rysunek obok). Do której łuzy wpadnie?
(rysunek obok). Do której łuzy wpadnie?
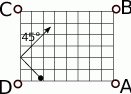
A) A B) B C) C D) D E) Bila nie wpadnie do żadnej z tych łuz
Drewniany sześcian wymiaru 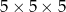 został zbudowany poprzez sklejenie ze sobą
został zbudowany poprzez sklejenie ze sobą 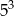 sześcianów jednostkowych. Kleofas sfotografował ten sześcian w taki sposób, aby na zdjęciu widać było największą możliwą liczbę sześcianów jednostkowych. Ile sześcianów jednostkowych było widocznych na zdjęciu wykonanym przez Kleofasa.
sześcianów jednostkowych. Kleofas sfotografował ten sześcian w taki sposób, aby na zdjęciu widać było największą możliwą liczbę sześcianów jednostkowych. Ile sześcianów jednostkowych było widocznych na zdjęciu wykonanym przez Kleofasa.
A) 75 B) 74 C) 60 D) 61 E) 62
Mam kwadrat o wymiarach 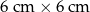 i trójkąt. Jeżeli położę kwadrat na trójkącie, to mogę pokryć co najwyżej 60% powierzchni trójkąta. Jeżeli zaś położę trójkąt na kwadracie, to mogę pokryć co najwyżej
i trójkąt. Jeżeli położę kwadrat na trójkącie, to mogę pokryć co najwyżej 60% powierzchni trójkąta. Jeżeli zaś położę trójkąt na kwadracie, to mogę pokryć co najwyżej  powierzchni kwadratu. Pole trójkąta jest równe
powierzchni kwadratu. Pole trójkąta jest równe
A) 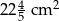 B)
B) 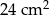 C)
C) 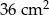 D)
D) 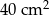 E)
E) 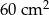
W czworokącie 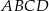 spełniony jest warunek
spełniony jest warunek 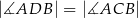 . Wykaż, że na czworokącie
. Wykaż, że na czworokącie 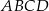 można opisać okrąg.
można opisać okrąg.
Na powitanie Nowego Roku Bartek założył koszulkę z nadrukiem jak na poniższym obrazku i stanął przed lustrem na rękach, z nogami uniesionymi pionowo w górę.
![]()
Co zobaczył w lustrze jego kolega Mikołaj, który stał (oczywiście na nogach) za Bartkiem?
![]()
Pięć liczb całkowitych rozmieszczono na okręgu. Okazało się, że dla każdych dwóch sąsiadujących ze sobą liczb, ani ich suma, ani suma pozostałych trzech nie jest podzielna przez 3. Ile wśród tych pięciu liczb jest podzielnych przez 3?
A) 0 B) 1 C) 2 D) 3 E) Nie można tego wyznaczyć
Punkt 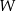 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 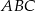 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 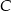 i
i 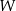 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie 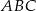 w punkcie
w punkcie 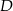 . Wykaż, że trójkąt
. Wykaż, że trójkąt 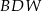 jest równoramienny.
jest równoramienny.
Czworokąt 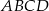 jest trapezem prostokątnym, w którym
jest trapezem prostokątnym, w którym 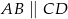 . Wykaż że
. Wykaż że
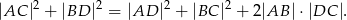
Wykaż, że jeżeli liczby dodatnie  i
i 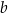 spełniają warunek
spełniają warunek
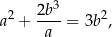
to spełniają też równość
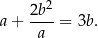
Ile trójkątów równoramiennych o polu równym 1 ma bok długości 2?
A) 0 B) 1 C) 2 D) 3 E) 4
Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 5 i 12 poprowadzono prostą, która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdź stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty.
Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 8 i 15 poprowadzono prostą, która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdź stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty.
Rozwiąż układ równań 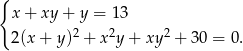
Kąt 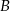 ma miarę o 25% mniejszą niż kąt
ma miarę o 25% mniejszą niż kąt 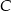 i o 50% większą niż kąt
i o 50% większą niż kąt 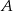 . Miara kąta
. Miara kąta 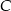 jest
jest
A) o 25% większa niż 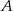
B) o 50% większa niż 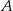
C) o 75% większa niż 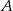
D) o 100% większa niż 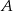
E) o 125% większa niż 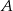
Niech 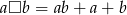 dla dowolnych liczb rzeczywistych
dla dowolnych liczb rzeczywistych 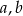 . Rozwiązaniem równania
. Rozwiązaniem równania 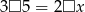 jest liczba
jest liczba
A) 3 B) 6 C) 7 D) 10 E) 12
Oblicz jakie długości powinny mieć boki prostokąta o polu równym 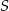 , aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
, aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
Państwo Kowalscy mają kilkoro dzieci. Średnia wieku rodziny Kowalskich wynosi 18 lat. Natomiast średnia wieku wszystkich członków rodziny bez ojca, który ma 38 lat, jest równa 14 lat. Ile dzieci jest w rodzinie Kowalskich?
A) 2 B) 3 C) 4 D) 5 E) 6
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 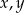 prawdziwa jest nierówność
prawdziwa jest nierówność
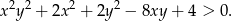
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 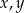 prawdziwa jest nierówność
prawdziwa jest nierówność
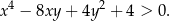
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 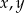 prawdziwa jest nierówność
prawdziwa jest nierówność
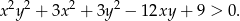
Arek, Bartek i Cyryl mają razem 30 piłeczek. Gdy Bartek dał 5 piłeczek Cyrylowi, Cyryl dał 4 piłeczki Arkowi, a Arek 2 Bartkowi, to okazało się, że chłopcy mają po tyle samo piłeczek. Ile piłeczek na początku miał Arek?
A) 8 B) 9 C) 11 D) 13 E) 15

