W trójkącie równoramiennym 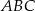 długość dwusiecznej
długość dwusiecznej 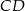 kąta przy wierzchołku
kąta przy wierzchołku 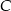 jest równa długości podstawy
jest równa długości podstawy 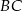 . Ile jest równa miara kąta
. Ile jest równa miara kąta 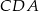 ?
?
A) 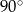 B)
B) 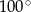 C)
C) 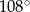 D)
D) 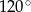 E) Nie da się tego rozstrzygnąć
E) Nie da się tego rozstrzygnąć
/Konkursy
Kwadrat o polu 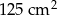 podzielono na pięć części o równych polach. Cztery z nich to kwadraty, a piąta to sześciokąt w kształcie litery L. Jaka jest długość najkrótszego boku tego sześciokąta?
podzielono na pięć części o równych polach. Cztery z nich to kwadraty, a piąta to sześciokąt w kształcie litery L. Jaka jest długość najkrótszego boku tego sześciokąta?

A) 1 cm B) 1,2 cm C) 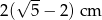 D)
D) 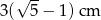 E)
E) 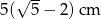
Dwa trójkąty równoboczne o obwodach po 18 cm nałożono na siebie tak, że odpowiednie pary ich boków są do siebie równoległe. Jaki jest obwód zacieniowanego sześciokąta?
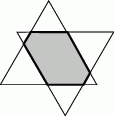
A) 9 cm B) 12 cm C) 13 cm D) 14 cm E) 18 cm
Udowodnij, że dla każdych dwóch liczb rzeczywistych 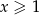 i
i 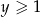 prawdziwa jest nierówność
prawdziwa jest nierówność
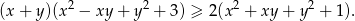
Udowodnij, że dla każdych dwóch liczb rzeczywistych 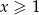 i
i 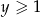 prawdziwa jest nierówność
prawdziwa jest nierówność
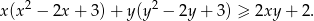
Znajdź wielomian o współczynnikach całkowitych, którego pierwiastkiem jest liczba 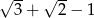 .
.
Wykaż, że jeżeli liczby rzeczywiste 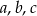 spełniają równość
spełniają równość 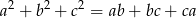 to
to 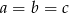 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 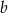 i
i  , funkcja
, funkcja
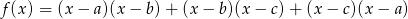
ma co najmniej jedno miejsce zerowe.
Środkowa 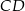 trójkąta
trójkąta 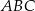 jest równa bokowi
jest równa bokowi 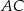 . Wyznacz kąty trójkąta
. Wyznacz kąty trójkąta 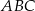 wiedząc, że
wiedząc, że 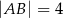 i
i 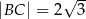 .
.
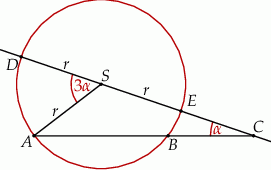
Dany jest okrąg o środku w punkcie 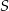 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 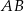 poza punkt
poza punkt 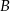 odłożono odcinek
odłożono odcinek 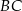 . Przez punkty
. Przez punkty 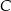 i
i 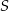 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 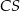 przecina dany okrąg w punktach
przecina dany okrąg w punktach 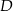 i
i 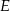 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 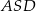 jest trzy razy większa od miary kąta
jest trzy razy większa od miary kąta 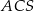 , to
, to 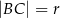 .
.
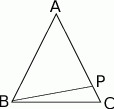
Rysunek obok przedstawia trójkąt równoramienny 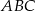 (
(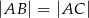 ), w którym
), w którym 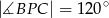 i
i 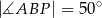 . Jaka jest miara kąta
. Jaka jest miara kąta 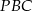 ?
?
A) 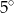 B)
B) 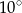 C)
C) 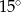 D)
D) 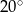 E)
E) 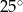
Wykaż, że wielomian 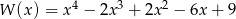 nie ma pierwiastków rzeczywistych.
nie ma pierwiastków rzeczywistych.
Z siatki składającej się z 8 trójkątów równobocznych można skleić ośmiościan foremny, jak na rysunku obok. Aby powstał ośmiościan magiczny, trzeba zamienić litery 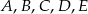 na liczby 2,4,6,7,8 (każdą literę na inną liczbę) w ten sposób, by sumy liczb na czterech ścianach przy każdym wierzchołku były sobie równe. Ile wówczas będzie równe
na liczby 2,4,6,7,8 (każdą literę na inną liczbę) w ten sposób, by sumy liczb na czterech ścianach przy każdym wierzchołku były sobie równe. Ile wówczas będzie równe 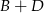 ?
?
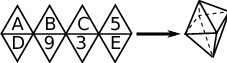
A) 6 B) 7 C) 8 D) 9 E) 10
Udowodnij, że jeżeli środki boków dwóch czworokątów wypukłych pokrywają się, to pola tych czworokątów są równe.
Na rysunku poniżej punkty 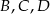 dzielą odcinek
dzielą odcinek 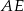 na cztery równe części. Narysowane trzy łuki są półokręgami o średnicach odpowiednio
na cztery równe części. Narysowane trzy łuki są półokręgami o średnicach odpowiednio 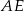 ,
, 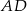 i
i 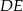 . Jaki jest stosunek długości półokręgu
. Jaki jest stosunek długości półokręgu 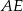 do sumy długości półokręgów
do sumy długości półokręgów 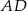 i
i 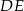 ?
?
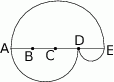
A) 1:2 B) 2:3 C) 2:1 D) 3:2 E) 1:1
Wykaż, że jeżeli liczba  jest sumą kwadratów dwóch liczb całkowitych, to liczba
jest sumą kwadratów dwóch liczb całkowitych, to liczba 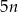 również ma tę własność.
również ma tę własność.
Uzasadnij, że równanie 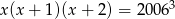 nie ma pierwiastków całkowitych.
nie ma pierwiastków całkowitych.
Dwóch korektorów, pracując razem, jest w stanie dokonać poprawek w tekście w czasie 8 godzin. Jeżeli każdy z nich wykonywałby tę pracę sam, to pierwszy, bardziej doświadczony korektor zakończyłby ją o 12 godzin wcześniej niż drugi. W ciągu ilu godzin każdy z korektorów wykonałby tę pracę samodzielnie?
Pierwsza pompa napełnia zbiornik w czasie o 15 godzin krótszym niż druga pompa. Jeżeli obie pompy pracują jednocześnie, to zbiornik zostaje napełniony w czasie 10 godzin. Ile godzin potrzeba na napełnienie zbiornika przy pomocy każdej z pomp?
Basen można napełnić dwoma kranami w ciągu 6 godzin. Pierwszy kran napełnia basen w czasie o 5 godzin krótszym niż drugi. W ciągu ilu godzin, każdy kran oddzielnie napełni basen.
Basen można napełnić dwoma kranami w ciągu 3 godzin. Pierwszy kran napełnia basen w czasie o 8 godzin krótszym niż drugi. W ciągu ilu godzin, każdy kran oddzielnie napełni basen.
Basen można napełnić, otwierając zawór nr 1, a opróżnić, odkręcając zawór nr 2. Jeśli otworzony jest tylko jeden zawór, całkowite napełnienie basenu trwa o godzinę krócej niż jego opróżnienie. Gdy równocześnie odkręcono obydwa zawory, basen napełnił się w ciągu 12 godzin. W ciągu ilu godzin napełni się basen, jeżeli zawór nr 2 będzie zamknięty?
Ile dróg prowadzi od górnego do dolnego końca przeciwprostokątnej dużego trójkąta, jeśli wolno poruszać się po bokach małych trójkątów w sposób przedstawiony na rysunku
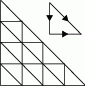
A) 16 B) 27 C) 64 D) 90 E) 111
Wszystkie potęgi liczby 3 oraz wszystkie te dodatnie liczby naturalne, które są skończonymi sumami różnych potęg liczby 3, ustawiamy w ciąg rosnący 1,3,4,9,10,12,13,…Ile jest równy setny wyraz tego ciągu?
A) 150 B) 981 C) 1234 D) 2401 E) 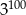
Starożytni Egipcjanie używali do wyznaczania kąta prostego linki z dwoma węzłami – złączone końce 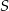 i
i 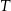 i owe węzły po naprężeniu linki tworzyły trójkąt prostokątny. Na takiej lince długości 12m węzeł
i owe węzły po naprężeniu linki tworzyły trójkąt prostokątny. Na takiej lince długości 12m węzeł 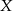 jest w odległości 3m od końca
jest w odległości 3m od końca 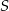 . W jakiej odległości od końca
. W jakiej odległości od końca 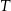 jest drugi węzeł, jeżeli po złączeniu końców otrzymujemy kąt prosty w węźle
jest drugi węzeł, jeżeli po złączeniu końców otrzymujemy kąt prosty w węźle 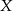 ?
?
![]()
A) 3m B) 4m C) 5m D) 6m E) Inna liczba

