W trójkącie 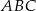 poprowadzono prostą
poprowadzono prostą 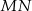 równoległą do prostej
równoległą do prostej 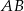 tak, że
tak, że 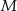 należy do
należy do 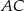 ,
, 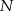 należy do
należy do 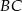 oraz
oraz 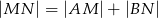 . Oblicz
. Oblicz 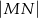 , jeśli
, jeśli 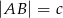 , a miary kątów trójkąta przy boku
, a miary kątów trójkąta przy boku 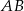 wynoszą
wynoszą  oraz
oraz 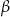 .
.
/Konkursy
Gwiazda, pokazana na rysunku obok, utworzona jest z 12 identycznych trójkątów równobocznych. Obwód gwiazdy jest równy 36 cm. Ile jest równy obwód zacieniowanego sześciokąta?
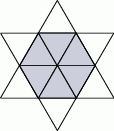
A) 6 cm B) 12 cm C) 18 cm D) 24 cm E) 30 cm
Udowodnij, że jeżeli 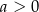 to dla wszystkich
to dla wszystkich 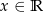 spełniona jest nierówność
spełniona jest nierówność 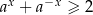 .
.
Na rysunku obok mamy trzy początkowe układanki. Ile jest potrzebnych białych kwadracików jednostkowych, aby ułożyć dziesiątą układankę w tym ciągu?
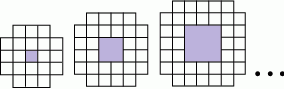
A) 76 B) 80 C) 84 D) 92 E) 100
Spośród trójkątów równoramiennych o ramionach długości 7 i podstawie, której długość wyraża się liczbą całkowitą, wybieramy trójkąt o największym obwodzie. Obwód ten jest równy
A) 14 B) 15 C) 21 D) 27 E) 28
Wykaż, że istnieją dokładnie dwie liczby naturalne  takie, że trójkąt o bokach
takie, że trójkąt o bokach 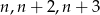 jest rozwartokątny.
jest rozwartokątny.
Malarz chcąc rozjaśnić 20 litrów granatowej farby postąpił w następujący sposób: odlał jeden litr farby i dolał 1 litr farby białej, a potem całość dokładnie wymieszał. Procedurę tę powtórzył w sumie 8 razy. Ile litrów granatowej farby pozostało w otrzymanej mieszaninie? Wynik podaj z dokładnością do 1 litra.
Uzasadnij, że jeżeli 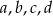 są liczbami dodatnimi to
są liczbami dodatnimi to
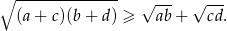
Wykaż, że dla 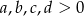 prawdziwa jest nierówność
prawdziwa jest nierówność 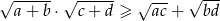 .
.
Ile z poniższych działań ma wartość różną od 6?
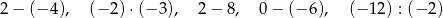
A) 0 B) 1 C) 2 D) 4 E) 5
Ile jest liczb dziesięciocyfrowych, które można napisać przy użyciu cyfr 1,2 i 3 tak, aby każde dwie sąsiednie cyfry w ich zapisach różniły się o jeden?
A) 16 B) 32 C) 64 D) 80 E) 100
Rozłożono 100 cukierków na 5 talerzach.
Na 1 i 2 talerzu znalazły się łącznie 52 cukierki,
na 2 i 3 talerzu 43 cukierki,
na 3 i 4 talerzu 34 cukierki,
na 4 i 5 talerzu 30 cukierków.
Ile cukierków znajdowało się na każdym talerzu?
Jakim procentem liczby elementów zboru 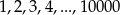 jest liczba tych jego elementów, które są kwadratami liczb naturalnych?
jest liczba tych jego elementów, które są kwadratami liczb naturalnych?
A) 1% B) 5% C) 10% D) 50% E) 0,1%
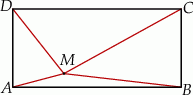
Punkt 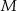 leży wewnątrz prostokąta
leży wewnątrz prostokąta 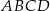 (zob. rysunek). Udowodnij, że
(zob. rysunek). Udowodnij, że 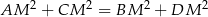 .
.
Różnica
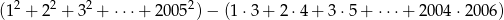
jest równa
A) 2000 B) 2004 C) 2005 D) 2006 E) 0
Niech  i
i 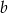 będą długościami kolejnych boków równoległoboku
będą długościami kolejnych boków równoległoboku 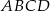 , zaś
, zaś 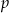 i
i  długościami jego przekątnych. Wykaż, że
długościami jego przekątnych. Wykaż, że 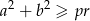 .
.
Ile jest liczb 2008–cyfrowych, których każde dwie kolejne cyfry tworzą liczbę podzielną przez 17 lub przez 23?
A) 5 B) 6 C) 7 D) 9 E) Więcej niż 9
Wykaż, że jeżeli w czworokącie 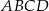 dwusieczne kątów przy wierzchołkach
dwusieczne kątów przy wierzchołkach 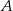 i
i 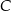 przecinają dwusieczne kątów przy wierzchołkach
przecinają dwusieczne kątów przy wierzchołkach 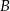 i
i 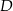 w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
W trójkącie równoramiennym dane są długości podstawy 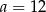 cm i wysokości
cm i wysokości 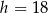 cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
Każdy kąt trójkąta 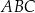 ma miarę mniejszą niż
ma miarę mniejszą niż 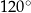 . Na bokach tego trójkąta zbudowano trójkąty równoboczne
. Na bokach tego trójkąta zbudowano trójkąty równoboczne 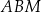 ,
, 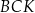 i
i 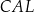 (zobacz rysunek).
(zobacz rysunek).
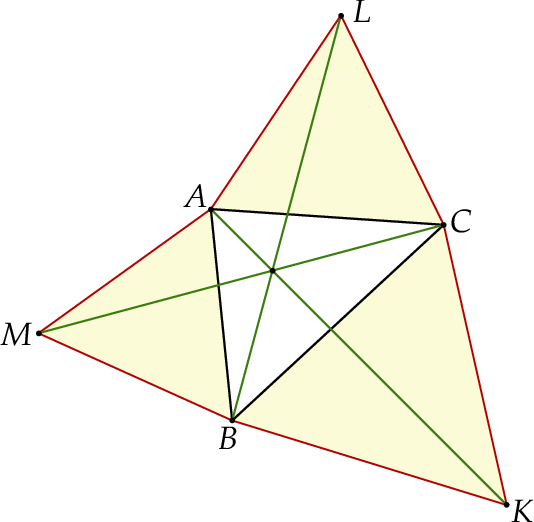
-
Wykaż, że
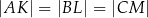 .
. -
Wykaż, że proste
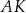 ,
, 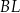 i
i 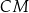 przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
Każda z liczb 257,338 ma tę własność, że jeśli jej cyfry zapiszemy w odwrotnej kolejności, to otrzymamy liczbę od niej większą. Ile jest wszystkich liczb trzycyfrowych o tej własności?
A) 124 B) 252 C) 280 D) 288 E) 360

