W sejfie przechowywana jest pewna liczba naszyjników. Wszystkie naszyjniki mają tę samą liczbę pereł (każdy ma ich co najmniej dwie). Liczba wszystkich pereł w tych naszyjnikach jest większa od 200, ale mniejsza od 300. Wiadomo, że znajomość liczby wszystkich pereł w tych naszyjnikach pozwala jednoznacznie określić liczbę tych naszyjników. Ile naszyjników znajduje się w sejfie?
A) 16 B) 17 C) 19 D) 25 E) Inna liczba
/Konkursy
Dany jest trapez prostokątny 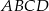 o podstawach
o podstawach 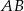 i
i 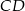 , w którym boki
, w którym boki 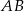 i
i 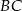 są prostopadłe. Dwusieczne kątów
są prostopadłe. Dwusieczne kątów 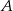 i
i 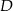 przecinają się w punkcie
przecinają się w punkcie 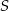 leżącym na boku
leżącym na boku 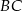 . Wykaż, że
. Wykaż, że 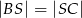 .
.
W trójkącie równoramiennym 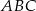 (
(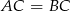 ) poprowadzono wysokości
) poprowadzono wysokości 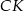 i
i 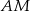 . Wiedząc że
. Wiedząc że 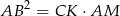 wyznacz cosinus kąta przy podstawie trójkąta.
wyznacz cosinus kąta przy podstawie trójkąta.
Świeżo skoszona trawa zawiera 60% wody, a wysuszone siano tylko 15% wody. Oblicz, ile kilogramów wysuszonego siana można otrzymać z 1 tony skoszonej trawy? Wynik podaj w zaokrągleniu do pełnych kilogramów.
Napisano liczbę o możliwie największej liczbie cyfr, w której każde dwie sąsiednie cyfry tworzą dwucyfrową liczbę będącą kwadratem pewnej liczby naturalnej. Ile cyfr ma ta liczba?
A) 5 B) 4 C) 3 D) 6 E) 10
Psa na smyczy o długości 10 m przywiązano do naroża budynku (patrz rysunek). Ile metrów ma obwód obszaru chronionego przez psa?
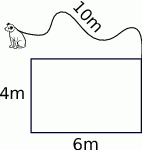
A) 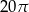 B)
B) 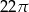 C)
C) 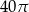 D)
D) 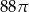 E)
E) 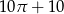
Mirek, Mietek i Piotr zbierali pieniądze na zakup namiotu. Mirek dał 60% potrzebnej kwoty, Mietek dał 40% pozostałej części. Piotr dołożył brakujące 30 zł. Ile kosztował namiot?
A) 50 zł B) 60 zł C) 125 zł D) 150 zł E) 200 zł
Udowodnij, że dla każdej liczby naturalnej  , liczba
, liczba 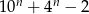 jest liczbą podzielną przez 3.
jest liczbą podzielną przez 3.
Jeśli 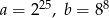 i
i 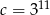 , to
, to
A) 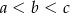 B)
B) 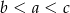 C)
C) 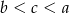 D)
D) 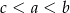 E)
E) 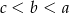
Z pierwszego sprawdzianu dostałem jedynkę. Z ilu sprawdzianów powinienem dostać piątkę, aby moja średnia była równa 4?
A) 2 B) 3 C) 4 D) 5 E) 6
Dany jest czworokąt wypukły 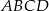 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 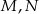 są odpowiednio środkami boków
są odpowiednio środkami boków 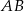 i
i 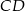 . Punkty
. Punkty 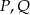 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 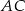 i
i 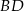 . Uzasadnij, że
. Uzasadnij, że 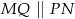 .
.
Dany jest czworokąt wypukły 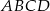 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 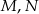 są odpowiednio środkami boków
są odpowiednio środkami boków 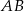 i
i 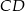 . Punkty
. Punkty 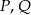 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 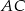 i
i 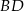 . Uzasadnij, że czworokąt
. Uzasadnij, że czworokąt 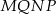 jest równoległobokiem.
jest równoległobokiem.
W prostokącie 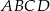 , w którym stosunek długości boków
, w którym stosunek długości boków 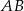 i
i 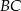 jest równy 4:3, poprowadzono dwusieczne kątów
jest równy 4:3, poprowadzono dwusieczne kątów 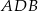 i
i 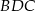 . Dwusieczne te przecinają boki
. Dwusieczne te przecinają boki 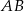 i
i 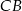 odpowiednio w punktach
odpowiednio w punktach 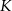 i
i 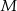 . Oblicz stosunek pola prostokąta
. Oblicz stosunek pola prostokąta 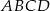 do pola trójkąta
do pola trójkąta 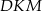 .
.
Wielokąt wypukły ma  wierzchołków,
wierzchołków, 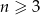 ,
, 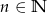 , spośród których losujemy jednocześnie dwa. Wyznacz
, spośród których losujemy jednocześnie dwa. Wyznacz  , wiedząc, że prawdopodobieństwo wylosowania wierzchołków wyznaczających przekątną tego wielokąta jest mniejsze od
, wiedząc, że prawdopodobieństwo wylosowania wierzchołków wyznaczających przekątną tego wielokąta jest mniejsze od 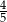 .
.
Średni wiek w pewnej sześcioosobowej grupie tematycznej na konferencji naukowej wynosił 49 lat. Najmłodszy uczestnik zrezygnował i wówczas średnia wieku wzrosła do 53 lat. Ile lat miał najmłodszy uczestnik?
Długość ramienia trapezu jest równa 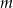 , a odległość od niego środka przeciwległego ramienia jest równa
, a odległość od niego środka przeciwległego ramienia jest równa 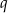 . Wyznacz pole trapezu.
. Wyznacz pole trapezu.
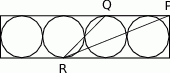
Cztery styczne okręgi o promieniu 6 cm zostały umieszczone w prostokącie jak na rysunku obok. Ile jest równe pole trójkąta 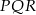 , jeśli
, jeśli 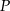 jest wierzchołkiem prostokąta, a
jest wierzchołkiem prostokąta, a 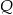 i
i 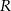 punktami styczności?
punktami styczności?
A) 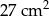 B)
B) 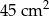 C)
C) 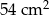 D)
D) 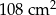 E)
E) 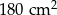
Punkty 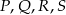 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 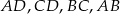 czworościanu
czworościanu 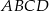 . Wykaż, że punkty
. Wykaż, że punkty 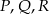 i
i 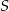 są wierzchołkami równoległoboku.
są wierzchołkami równoległoboku.
Ile jest równa suma oczek na niewidocznych ściankach kostek do gry?
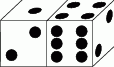
A) 15 B) 12 C) 7 D) 27 E) inna odpowiedź.
Punkt 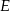 jest środkiem boku
jest środkiem boku 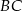 prostokąta
prostokąta 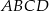 , w którym
, w którym 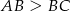 . Punkt
. Punkt 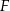 leży na boku
leży na boku 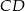 tego prostokąta oraz
tego prostokąta oraz 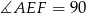 . Udowodnij, że
. Udowodnij, że 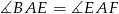 .
.
Wiadomo, że 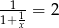 . Wówczas wartość wyrażenia
. Wówczas wartość wyrażenia 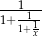 jest równa
jest równa
A)  B)
B) 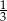 C)
C)  D)
D) 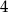 E)
E)