Wiadomo, że jeżeli kangurek Skoczek odbija się lewą nogą, to jego skok ma długość 2 m. Jeżeli odbija się prawą nogą, to skok ma długość 4 m. Gdy Skoczek odbija się obiema nogami, to skacze na odległosć 7 m. Jaką najmniejszą liczbę skoków musi wykonać Skoczek, aby przebyć odległość równą dokładnie 1000 m?
A) 140 B) 144 C) 175 D) 176 E) 150
/Konkursy
Dany jest taki czworokąt wypukły 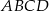 , że okręgi wpisane w trójkąty
, że okręgi wpisane w trójkąty 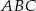 i
i 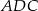 są styczne. Wykaż, że w czworokąt
są styczne. Wykaż, że w czworokąt 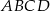 można wpisać okrąg.
można wpisać okrąg.
Aby otrzymać liczbę 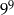 , należy liczbę
, należy liczbę 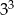 podnieść do potęgi
podnieść do potęgi
A) 2 B) 3 C) 6 D) 9 E) 18
Dany jest kwadrat 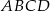 . Odcinki poprowadzone z punktów
. Odcinki poprowadzone z punktów 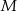 i
i 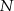 do jego wierzchołków dzielą go na osiem części. Na rysunku zaznaczono pola trzech z nich. Jakie jest pole zacieniowanej części?
do jego wierzchołków dzielą go na osiem części. Na rysunku zaznaczono pola trzech z nich. Jakie jest pole zacieniowanej części?
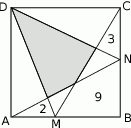
A) 14 B) 18 C) 11 D) 12 E) 9
W okrąg wpisany jest trójkąt 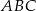 , przy czym
, przy czym 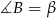 i
i 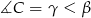 . Oblicz miarę kąta między prostą
. Oblicz miarę kąta między prostą 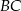 i styczną do okręgu w punkcie
i styczną do okręgu w punkcie 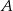 .
.
Trójkąt prostokątny 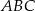 ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.
ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.
Wykaż, że jeśli  należy do zbioru liczb całkowitych, to
należy do zbioru liczb całkowitych, to 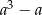 jest podzielne przez 3.
jest podzielne przez 3.
Udowodnij, że w czworokącie wpisanym w okrąg suma iloczynów długości przeciwległych boków jest równa iloczynowi długości przekątnych (twierdzenie Ptolemeusza).
Michał na egzaminie testowym odpowiedział poprawnie na 80% pytań, a na pozostałe 5 pytań nie udzielił odpowiedzi. Ile było pytań w teście?
A) 20 B) 25 C) 30 D) 35 E) 40
Pięcioosobowe zespoły z dwóch szkół mają rozegrać pomiędzy sobą zawody w tenisie stołowym par. Każda para zawodników jednej szkoły musi rozegrać z każdą parą zawodników z drugiej szkoły dokładnie jedno spotkanie. W ilu spotkaniach zagra każdy z 10 zawodników?
A) 10 B) 20 C) 30 D) 40 E) 50
Uczeń ma 2009 sześciennych klocków o krawędzi długości 1 oraz 2009 kolorowych kwadratowych naklejek o boku długości 1. Uczeń ten skleił ze wszystkich klocków prostopadłościan i okleił całą jego powierzchnię naklejkami, przyklejając dokładnie po jednej do każdej ściany klocka, tworzącej tę powierzchnię. Okazało się, że uczniowi pozostały jeszcze naklejki. Ile ich pozostało?
A) Więcej niż 1000 B) 763 C) 476 D) 49 E) Opisana sytuacja jest niemożliwa
Wyznacz wszystkie pary liczb całkowitych 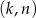 spełniających równość
spełniających równość 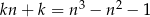 .
.
W równości 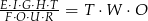 różnym literom odpowiadają różne cyfry, a jednakowym literom jednakowe cyfry. Ile wartości może przyjmować iloczyn
różnym literom odpowiadają różne cyfry, a jednakowym literom jednakowe cyfry. Ile wartości może przyjmować iloczyn 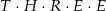 ?
?
A) 1 B) 2 C) 3 D) 4 E) 5
Ile jest liczb całkowitych dodatnich, których kwadrat i sześcian mają tę samą liczbę cyfr w zapisach w systemie dziesiątkowym?
A) 0 B) 3 C) 4 D) 9 E) Nieskończenie wiele.
75% połowy  liczby 240 jest równe
liczby 240 jest równe
A) 120 B) 90 C) 80 D) 60 E) 40
Wyznacz wszystkie pary 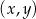 , gdzie
, gdzie  i
i 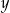 są liczbami całkowitymi spełniającymi równanie
są liczbami całkowitymi spełniającymi równanie
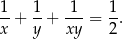
W każde pole tablicy o wymiarach 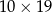 wpisujemy 0 lub 1. Wyznaczamy sumy liczb stojących w każdym wierszu i w każdej kolumnie. Największa możliwa liczba różnych sum, które można w ten sposób otrzymać, jest równa
wpisujemy 0 lub 1. Wyznaczamy sumy liczb stojących w każdym wierszu i w każdej kolumnie. Największa możliwa liczba różnych sum, które można w ten sposób otrzymać, jest równa
A) 9 B) 10 C) 15 D) 19 E) 29
Czworokąt 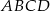 jest trapezem o podstawach
jest trapezem o podstawach 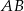 i
i 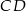 . Wykaż że
. Wykaż że
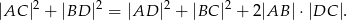
Jedna z podstaw trapezu wpisanego w okrąg jest średnicą okręgu. Oblicz cosinus kąta ostrego trapezu wiedząc, że stosunek obwodu trapezu do sumy długości jego podstaw wynosi 3:2.
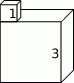
Bryła widoczna na rysunku obok jest zbudowana z dwóch sześcianów o krawędziach długości 1 cm i 3 cm. Jakie jest pole powierzchni tej bryły?
A) 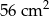 B)
B) 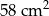 C)
C) 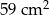 D)
D) 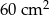 E)
E)