Kąt ostry rombu 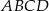 ma miarę
ma miarę 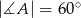 . Na bokach
. Na bokach 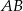 i
i 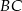 wybrano punkty
wybrano punkty 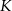 i
i 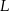 w ten sposób, że
w ten sposób, że 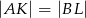 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 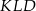 jest trójkątem równobocznym.
jest trójkątem równobocznym.
/Konkursy
Wyspę zamieszkują kłamcy i prawdomówni (kłamcy zawsze kłamią, a prawdomówni zawsze mówią prawdę). Pewnego dnia zebrało się 12 wyspiarzy, wśród których byli kłamcy i prawdomówni i wygłosiło kilka stwierdzeń. Dwóch z nich powiedziało: „Dokładnie dwie osoby wśród nas dwunastu to kłamcy”. Każda z następnych czterech osób powiedziała: „Dokładnie cztery osoby wśród nas dwunastu to kłamcy”. Natomiast każda z pozostałych sześciu osób stwierdziła: „Dokładnie sześć osób wśród nas dwunastu to kłamcy". Ilu jest kłamców wśród tej dwunastki wyspiarzy?
A) 2 B) 4 C) 6 D) 8 E) 10
Liczby naturalne  i
i 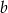 spełniają równość
spełniają równość 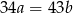 . Udowodnij, że liczba
. Udowodnij, że liczba 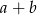 jest złożona.
jest złożona.
Wykaż, że proste przechodzące przez wierzchołek równoległoboku i środki boków, do których on nie należy, dzielą przekątną równoległoboku na trzy równe części.
Wykaż, że w dowolnym równoległoboku suma kwadratów długości przekątnych jest równa sumie kwadratów długości wszystkich boków.
Dwie pracownice urzędu pocztowego miały ostemplować pewną partię listów. Stemplowanie listów pierwsza urzędniczka rozpoczęła o godzinie 8:00, a druga o godzinie 9:00. O godzinie 11:00 panie stwierdziły, że pozostało im jeszcze do ostemplowania 45% listów. Po ukończeniu pracy okazało się, że każda z urzędniczek ostemplowała tyle samo listów. Oblicz, w ciągu ilu godzin każda z pań ostemplowałaby sama wszystkie listy.
Udowodnij że jeśli dwie dwusieczne w trójkącie są sobie równe to trójkąt jest równoramienny (twierdzenie Steinera-Lehmusa).
Wyznacz wszystkie liczby całkowite  , dla których liczba
, dla których liczba 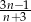 jest liczbą całkowitą.
jest liczbą całkowitą.
Planujemy pokolorować kratki kwadratu, używając kolorów 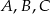 i
i 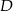 w taki sposób, by żadne dwie kratki o wspólnym boku lub wierzchołku nie były pokolorowane tym samym kolorem. Pewne kratki są już pokolorowane (patrz rysunek).
w taki sposób, by żadne dwie kratki o wspólnym boku lub wierzchołku nie były pokolorowane tym samym kolorem. Pewne kratki są już pokolorowane (patrz rysunek).

Jakie są możliwe pokolorowania kratki zacieniowanej?
A) Tylko 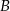 . B) Tylko
. B) Tylko 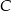 . C) Tylko
. C) Tylko 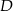 . D) Albo
. D) Albo 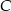 , albo
, albo 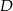 .
.
E) Kwadratu tego nie można tak pokolorować.
Znajdź wszystkie funkcje 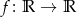 , dla których zachodzi równość
, dla których zachodzi równość 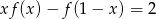 .
.
Dwa okręgi przecinają się w punktach 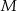 i
i 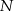 . Przez punkt
. Przez punkt 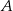 pierwszego okręgu prowadzimy proste
pierwszego okręgu prowadzimy proste 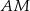 i
i 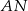 , przecinające drugi okrąg w punktach
, przecinające drugi okrąg w punktach 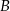 i
i 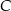 . Udowodnij, że styczna w punkcie
. Udowodnij, że styczna w punkcie 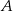 do pierwszego okręgu jest równoległa do prostej
do pierwszego okręgu jest równoległa do prostej 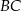 .
.
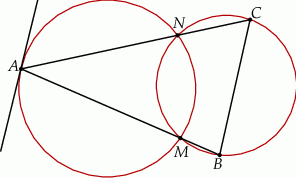
Dwa okręgi przecinają się w punktach 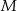 i
i 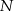 . Przez punkt
. Przez punkt 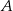 pierwszego okręgu prowadzimy proste
pierwszego okręgu prowadzimy proste 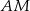 i
i 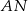 , przecinające drugi okrąg w punktach
, przecinające drugi okrąg w punktach 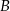 i
i 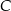 . Udowodnij, że styczna w punkcie
. Udowodnij, że styczna w punkcie 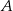 do pierwszego okręgu jest równoległa do prostej
do pierwszego okręgu jest równoległa do prostej 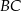 .
.
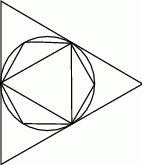
Trójkąt równoboczny i sześciokąt foremny wpisano w okrąg, na którym opisano trójkąt równoboczny (patrz rysunek). Niech 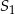 oznacza pole dużego trójkąta,
oznacza pole dużego trójkąta, 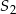 pole małego trójkąta, a
pole małego trójkąta, a 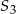 pole sześciokąta foremnego. Która z równości jest prawdziwa?
pole sześciokąta foremnego. Która z równości jest prawdziwa?
A) 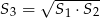 B)
B) 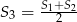 C)
C) 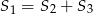 D)
D) 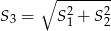 E)
E) 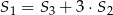
Wyspę zamieszkują prawdomówni i kłamcy. Prawdomówni zawsze mówią prawdę, a kłamcy zawsze kłamią. 25 mieszkańców tej wyspy ustawiło się w kolejkę. Każda osoba z kolejki, z wyjątkiem pierwszej, powiedziała: Osoba stojąca bezpośrednio przede mną to kłamca, natomiast osoba stojąca jako pierwsza w kolejce powiedziała: Wszyscy stojący za mną to kłamcy. Ilu kłamców stało w tej kolejce?
A) 24 B) 13 C) 12 D) 0 E) Nie można obliczyć
Wyznacz miary kątów trójkąta, w którym wysokość i środkowa poprowadzona z jednego wierzchołka dzielą kąt przy tym wierzchołku na 3 równe części.
Wyznacz wszystkie liczby całkowite 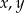 spełniające równanie
spełniające równanie 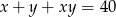 .
.
Obwód trójkąta 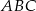 jest równy 8. Oblicz obwód trójkąta
jest równy 8. Oblicz obwód trójkąta 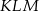 o wierzchołkach będących środkami środkowych trójkąta
o wierzchołkach będących środkami środkowych trójkąta 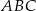 .
.
W pewnej szkole 40 uczniów to członkowie SKS-u. Wśród nich 26 gra w siatkówkę, 25 pływa, a 27 jeździ na nartach. Jednocześnie pływa i gra w siatkówkę 15 uczniów, gra w siatkówkę i jeździ na nartach 16, a pływa i jeździ na nartach 18. Jeden uczeń nie zajmuje się sportem. Ilu uczniów uprawia wszystkie trzy dyscypliny sportowe? Ilu uczniów uprawia tylko jedną dyscyplinę sportową?
W kwadracie o boku długości 1 narysowano dwa okręgi jak na rysunku. Jaką wartość ma suma długości promieni tych okręgów?

A) 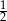
B) 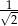
C) 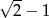
D) 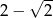
E) Suma ta zależy od stosunku promieni tych okręgów
W pewnym trapezie kąty przy dwóch przeciwległych wierzchołkach mają miary  oraz
oraz 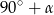 . Jedno z ramion tego trapezu ma długość
. Jedno z ramion tego trapezu ma długość 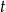 . Wyznacz różnicę długości podstaw tego trapezu.
. Wyznacz różnicę długości podstaw tego trapezu.
Podstawy trapezu 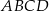 mają długości
mają długości 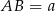 i
i 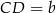 . Oblicz długość odcinka łączącego środki ramion trapezu.
. Oblicz długość odcinka łączącego środki ramion trapezu.

