Dany jest czworokąt wypukły 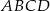 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 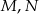 są odpowiednio środkami boków
są odpowiednio środkami boków 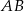 i
i 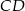 . Punkty
. Punkty 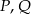 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 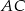 i
i 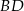 . Uzasadnij, że jeżeli odcinki
. Uzasadnij, że jeżeli odcinki 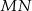 i
i 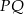 są prostopadłe, to
są prostopadłe, to 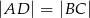 .
.
/Konkursy
Wykaż, że jeżeli odcinki łączące środki przeciwległych boków czworokąta są prostopadłe, to przekątne tego czworokąta mają równe długości.
Udowodnij, że różnica sześcianów dwóch kolejnych liczb całkowitych nie jest liczbą podzielną przez 5.
Punkt 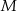 przyprostokątnej
przyprostokątnej 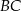 trójkąta prostokątnego
trójkąta prostokątnego 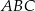 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 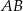 otrzymując punkt
otrzymując punkt 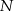 . Wykaż, że
. Wykaż, że 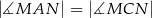 .
.
Dwusieczna kąta 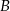 trójkąta
trójkąta 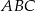 przecina bok
przecina bok 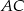 w punkcie
w punkcie 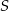 , a dwusieczna kąta
, a dwusieczna kąta 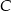 przecina bok
przecina bok 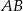 w punkcie
w punkcie 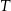 . Dwusieczne przecinają się w punkcie
. Dwusieczne przecinają się w punkcie 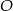 . Znajdź miarę kąta
. Znajdź miarę kąta 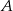 , jeżeli wiadomo, że na czworokącie
, jeżeli wiadomo, że na czworokącie 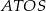 można opisać okrąg.
można opisać okrąg.
Wielomian 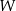 jest wielomianem stopnia 5 i spełnia warunki:
jest wielomianem stopnia 5 i spełnia warunki: 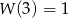 oraz
oraz 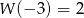 . Wykaż, że nie wszystkie współczynniki wielomianu
. Wykaż, że nie wszystkie współczynniki wielomianu 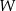 są liczbami całkowitymi.
są liczbami całkowitymi.
Liczby 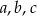 są rozwiązaniami równania
są rozwiązaniami równania 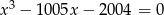 . Napisz równanie którego rozwiązaniami są liczby
. Napisz równanie którego rozwiązaniami są liczby 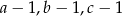 .
.
Dany jest równoległobok 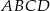 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 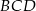 jest styczny do przekątnej
jest styczny do przekątnej 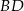 w punkcie
w punkcie 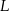 , a okrąg wpisany w trójkąt
, a okrąg wpisany w trójkąt 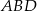 ma środek
ma środek 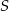 i jest styczny do boku
i jest styczny do boku 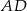 w punkcie
w punkcie 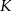 .
.
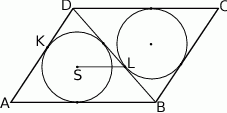
Wykaż, że jeżeli odcinek 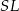 jest równoległy do prostej
jest równoległy do prostej 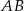 , to
, to 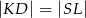 .
.
Dane są cztery okręgi. Każdy z nich jest styczny zewnętrznie do dokładnie dwóch spośród trzech pozostałych okręgów. Udowodnij, że punkty styczności tych okręgów są wierzchołkami czworokąta, na którym można opisać okrąg.
Która z liczb jest największa?
A) 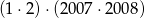
B) 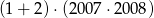
C) 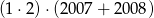
D) 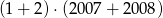
E) 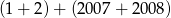
Znajdź wszystkie liczby całkowite dodatnie  , dla których liczba
, dla których liczba 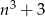 jest podzielna przez
jest podzielna przez 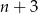 .
.
Uzasadnij, że jeśli 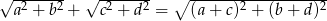 to
to 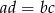 .
.
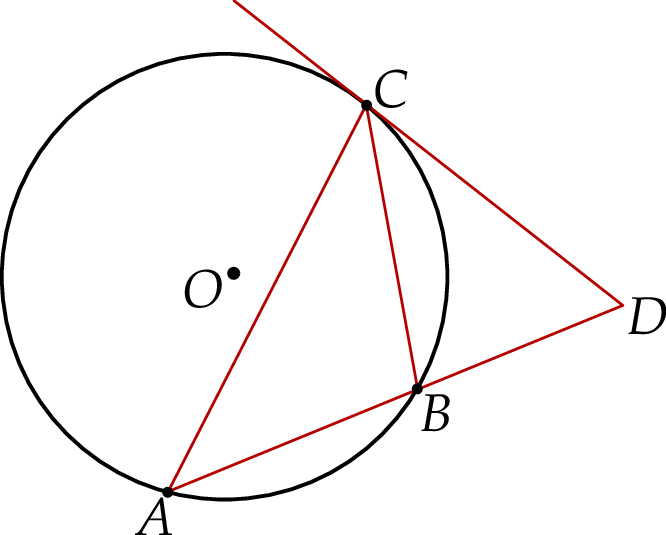
Prosta 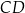 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 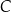 . Uzasadnij, że jeśli
. Uzasadnij, że jeśli 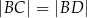 , to
, to 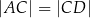 .
.
W trójkącie równoramiennym 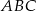 , w którym
, w którym 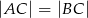 , poprowadzono dwusieczną
, poprowadzono dwusieczną 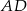 kąta przy wierzchołku
kąta przy wierzchołku 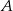 (patrz rysunek), przy czym
(patrz rysunek), przy czym 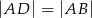 . Jaka jest miara kąta
. Jaka jest miara kąta 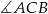 ?
?
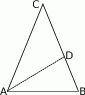
A) 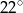 B)
B) 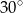 C)
C) 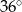 D)
D) 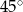 E)
E) 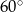
Na płaszczyźnie zaznaczono punkty 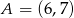 ,
, 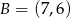 ,
, 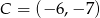 ,
, 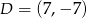 i
i 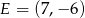 . Który z poniższych odcinków jest równoległy do osi
. Który z poniższych odcinków jest równoległy do osi 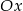 ?
?
A) 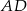 B)
B) 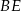 C)
C) 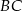 D)
D) 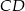 E)
E) 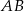
Na bokach 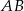 i
i 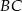 trójkąta ostrokątnego
trójkąta ostrokątnego 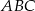 opisano, jako na średnicach, dwa okręgi. Gdzie leży punkt przecięcia się tych okręgów (różny od punktu B)?
opisano, jako na średnicach, dwa okręgi. Gdzie leży punkt przecięcia się tych okręgów (różny od punktu B)?
Andrzej, Mietek i Zbyszek rzucają kolejno kostką do gry. Andrzej wygrywa, jeżeli wyrzuci 1,2 lub 3. Mietek wygrywa, jeżeli wyrzuci 4 lub 5. Zbyszek wygrywa, jeżeli wyrzuci 6. Najpierw kostką rzuca Andrzej, potem Mietek, potem Zbyszek, potem znowu Andrzej, znowu Mietek, itd. Gra się kończy, gdy któryś z nich wygra. Jakie jest prawdopodobieństwo, że wygra Zbyszek?
A)  B)
B)  C)
C) 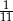 D)
D) 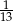 E) 0
E) 0
Cztery miasta 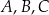 i
i 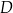 znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. Jeden z węzłów ma ma być połączony z miastami
znajdują się w wierzchołkach kwadratu o boku 300 km. Pewna firma dostała zlecenie na zaprojektowanie sieci dróg, która będzie łączyć każde dwa z tych miast. Sieć ma posiadać dwa węzły, a łączna długość dróg w sieci ma być możliwie najmniejsza. Jeden z węzłów ma ma być połączony z miastami 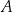 i
i 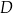 , a drugi węzeł z miastami
, a drugi węzeł z miastami 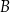 i
i 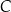 (zobacz rysunek).
(zobacz rysunek).
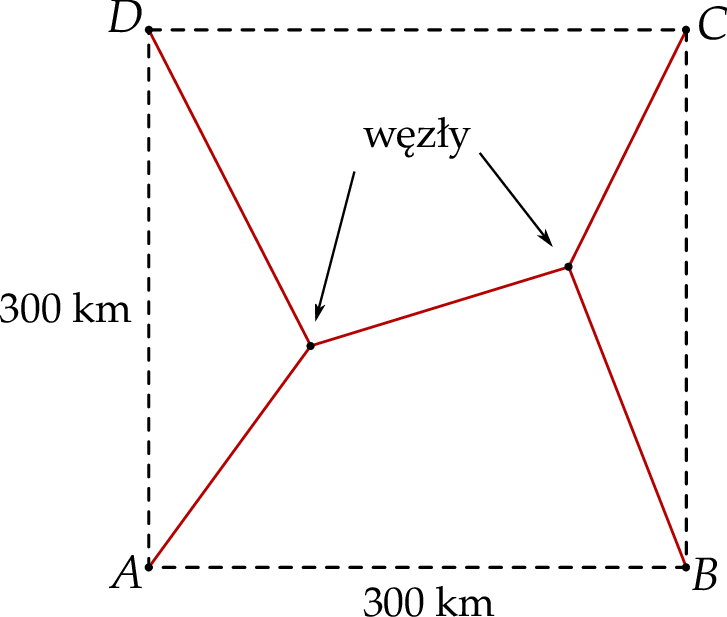
Oblicz, jaka musi być długość najkrótszej takiej sieci dróg i gdzie muszą być zlokalizowane węzły tej sieci.
Przekątne trapezu przecinają się w punkcie 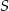 . Przez punkt
. Przez punkt 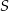 poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach
poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach 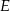 i
i 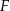 . Wykaż, że
. Wykaż, że 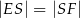 .
.
W trapezie 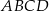 o podstawach
o podstawach 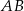 i
i 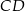 przez punkt
przez punkt 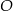 przecięcia się przekątnych poprowadzono dwie proste równoległe do boków
przecięcia się przekątnych poprowadzono dwie proste równoległe do boków 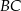 i
i 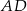 . Prosta równoległa do boku
. Prosta równoległa do boku 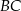 przecina bok
przecina bok 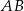 w punkcie
w punkcie 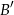 , a prosta równoległa do boku
, a prosta równoległa do boku 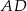 przecina bok
przecina bok 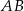 w punkcie
w punkcie 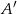 . Wykaż, że
. Wykaż, że 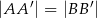 .
.
Piotrek kupił 3 rodzaje ciastek: duże, średnie i małe. Duże ciastko kosztuje 4 zł za sztukę, średnie po 2 zł, a małe po 1 zł. Piotrek kupił łącznie 10 ciastek za które zapłacił 16 zł. Ile kupił dużych ciastek?
W wyniku ankiety przeprowadzonej z udziałem 2006 uczestników stwierdzono, że 1500 spośród nich uczestniczyło w konkursie „Kangur Matematyczny”, a 1200 w konkursie języka angielskiego. Ilu uczestników ankiety brało udział w obydwu konkursach, jeżeli wiadomo, że 6 ankietowanych nie wzięło udziału w żadnym z konkursów?
A) 300 B) 500 C) 600 D) 700 E) 1000

