W kwadrat 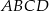 o boku długości
o boku długości 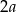 wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek
wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek 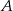 ze środkiem boku
ze środkiem boku 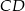 .
.
/Konkursy
Ojciec i syn postanowili zmierzyć odległość między dwoma drzewami za pomocą swoich kroków. Długość kroku ojca wynosi 70 cm, a długość kroku syna 56 cm. Jaka jest odległość między drzewami, jeśli ojciec i syn rozpoczęli pomiar w tym samym miejscu, a ślady ich stóp pokryły się 11 razy?
Jacek w ramach przygotowań do konkursu „Kangur Matematyczny” postanowił rozwiązać po jednym zadaniu z kolejnych stron o numerach nieparzystych w swoim zbiorze zadań. Rozpoczął na stronie 15, a skończył na stronie na stronie 53. Ile zadań treningowych rozwiązał Jacek?
A) 19 B) 20 C) 27 D) 38 E) 53
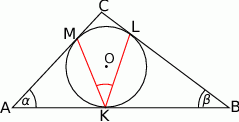
W trójkąt 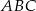 , w którym
, w którym 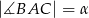 oraz
oraz 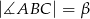 , wpisano okrąg. Punkty
, wpisano okrąg. Punkty 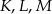 są punktami styczności okręgu odpowiednio z bokami
są punktami styczności okręgu odpowiednio z bokami 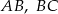 i
i 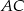 . Wykaż, że
. Wykaż, że 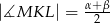 .
.
W półkole o średnicy 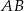 wpisano okrąg styczny do średnicy
wpisano okrąg styczny do średnicy 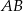 w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu
w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu 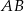 , do wpisanego okręgu oraz do średnicy
, do wpisanego okręgu oraz do średnicy 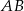 jeżeli
jeżeli 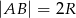 .
.
Liczbą dodatnią, której kwadrat jest większy od niej o 500% jest
A) 5 B) 6 C) 7 D) 8 E) 10
Wykaż że jeżeli 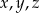 są liczbami rzeczywistymi oraz
są liczbami rzeczywistymi oraz 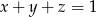 , to
, to 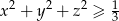 .
.
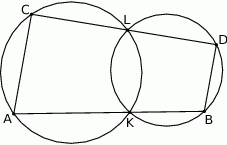
Dwa okręgi przecinają się w punktach 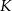 i
i 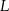 . Przez punkty
. Przez punkty 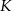 i
i 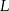 poprowadzono proste, które przecinają dane okręgi w punktach
poprowadzono proste, które przecinają dane okręgi w punktach 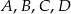 tak, jak pokazano to na poniższym rysunku. Wykaż, że
tak, jak pokazano to na poniższym rysunku. Wykaż, że 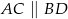 .
.
Jaka jest największa liczba cyfr, które należy usunąć z 1000-cyfrowej liczby 20082008…2008, aby suma pozostałych cyfr była równa 2008?
A) 260 B) 510 C) 520 D) 749 E) 746
Asi zerwał się naszyjnik. Trzecią część liczby korali znalazła na podłodze, jedną czwartą w kieszeni, jedną piątą pod oparciem kanapy, a szósta część liczby korali została na sznurku. Sześciu korali nie udało się jej odnaleźć. Oblicz, ile korali zostało na sznurku.
Udowodnij, że jeżeli 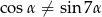 i
i 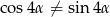 to
to
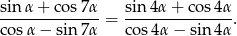
Pierścienie boromejskie to takie trzy pierścienie, których nie można rozdzielić bez rozcinania, ale po usunięciu któregokolwiek z nich pozostałe dwa nie są ze sobą powiązane w żaden sposób. Który z rysunków przedstawia pierścienie boromejskie?

Udowodnij, że w trapezie, który ma dwa kąty ostre przy jednej z podstaw, suma kwadratów przekątnych równa jest sumie podwojonego iloczynu dwóch boków równoległych i kwadratów pozostałych boków.
Przedstaw liczbę 20 jako sumę trzech liczb dodatnich tak, aby iloczyn tych liczb był jak największy.
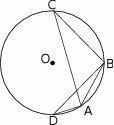
Trójkąty 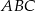 i
i 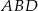 zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że
zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że 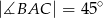 oraz
oraz 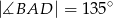 . Wówczas długości cięciw
. Wówczas długości cięciw 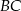 i
i 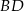 spełniają zależność
spełniają zależność
A) 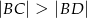
B) 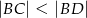
C) 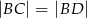
D) 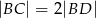
E) 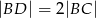
Dwa okręgi o promieniach  i
i 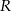 (
(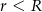 ) są styczne zewnętrznie. Prosta
) są styczne zewnętrznie. Prosta 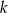 nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej
nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej 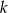 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.
Dane są dwa kąty wpisane oparte na tym samym łuku. Wykaż, że dwusieczne tych kątów przetną się w punkcie należącym do okręgu.
Do zbiornika o pojemności 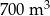 można doprowadzić wodę dwiema rurami. W ciągu jednej godziny pierwsza rura dostarcza do zbiornika o
można doprowadzić wodę dwiema rurami. W ciągu jednej godziny pierwsza rura dostarcza do zbiornika o 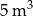 wody więcej niż druga rura. Czas napełniania zbiornika tylko pierwszą rurą jest o 16 godzin krótszy od czasu napełniania tego zbiornika tylko drugą rurą. Oblicz, w ciągu ilu godzin pusty zbiornik zostanie napełniony, jeśli woda będzie doprowadzana przez obie rury jednocześnie.
wody więcej niż druga rura. Czas napełniania zbiornika tylko pierwszą rurą jest o 16 godzin krótszy od czasu napełniania tego zbiornika tylko drugą rurą. Oblicz, w ciągu ilu godzin pusty zbiornik zostanie napełniony, jeśli woda będzie doprowadzana przez obie rury jednocześnie.
Do zbiornika o pojemności 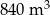 można doprowadzić wodę dwiema rurami. W ciągu jednej godziny pierwsza rura dostarcza do zbiornika o
można doprowadzić wodę dwiema rurami. W ciągu jednej godziny pierwsza rura dostarcza do zbiornika o 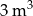 wody więcej niż druga rura. Czas napełniania zbiornika tylko pierwszą rurą jest o 32 godziny krótszy od czasu napełniania tego zbiornika tylko drugą rurą. Oblicz, w ciągu ilu godzin pusty zbiornik zostanie napełniony, jeśli woda będzie doprowadzana przez obie rury jednocześnie.
wody więcej niż druga rura. Czas napełniania zbiornika tylko pierwszą rurą jest o 32 godziny krótszy od czasu napełniania tego zbiornika tylko drugą rurą. Oblicz, w ciągu ilu godzin pusty zbiornik zostanie napełniony, jeśli woda będzie doprowadzana przez obie rury jednocześnie.
Na rysunku obok mały kwadrat wpisano w duży kwadrat. Pole małego kwadratu jest równe
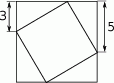
A) 16 B) 28 C) 34 D) 36 E) 49
W matematycznej pajęczynie na rysunku obok długości wszystkich odcinków wyrażają się liczbami całkowitymi. Ile jest równe  ?
?
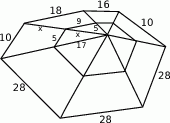
A) 11 B) 13 C) 15 D) 17 E) 19

