Pole trapezu jest równe 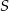 , a stosunek długości jego podstaw wynosi
, a stosunek długości jego podstaw wynosi 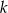 . Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
. Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
/Konkursy
Na rysunku obok dwa sześciokąty foremne mają wspólny bok. Jaka część pola równoległoboku jest zacieniowana?

A) 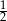 B)
B) 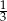 C)
C) 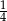 D)
D) 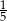 E)
E) 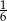
W kole o środku 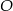 poprowadzono dwie prostopadłe średnice
poprowadzono dwie prostopadłe średnice 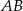 i
i 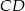 oraz cięciwę
oraz cięciwę 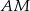 przecinającą średnicę
przecinającą średnicę 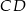 w punkcie
w punkcie 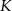 . Oblicz miarę kąta
. Oblicz miarę kąta 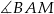 wiedząc, że w czworokąt
wiedząc, że w czworokąt 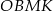 można wpisać okrąg.
można wpisać okrąg.
Na powierzchni piłki namalowano trzy jednakowe okręgi, dzielące ją na osiem jednakowych części, jak na rysunku obok. Trzmiel, który usiadł na piłce w punkcie przecięcia okręgów, wędruje po namalowanych okręgach w taki sposób, że po przejściu ćwiartki okręgu w punkcie przecięcia z innym okręgiem zawsze skręca na przemian w w prawo albo w lewo, tj. w prawo, gdy w poprzedzającym punkcie skręcał w lewo, natomiast w lewo, gdy w poprzedzającym punkcie skręcał w prawo. Jaka jest najmniejsza liczba ćwiartek okręgów, które musi przejść trzmiel aby ponownie znalazł się w punkcie, z którego wyruszył?
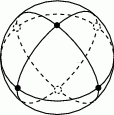
A) 6 B) 9 C) 12 D) 15 E) 18
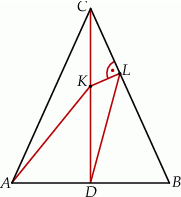
W trójkącie 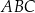 dwusieczna kąta
dwusieczna kąta 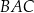 przecina bok
przecina bok 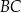 trójkąta w punkcie
trójkąta w punkcie 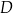 . Wykaż, że
. Wykaż, że
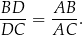
Trójkąty  i
i 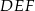 wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
Która liczba jest większa 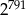 , czy
, czy 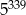 ?
?
Która liczba jest większa 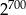 , czy
, czy 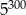 ?
?
W pokoju bawią się koty i psy. Liczba kocich łap jest dwa razy większa niż liczba psich nosów. Liczba kotów jest
A) dwa razy większa od liczby psów.
B) równa liczbie psów.
C) równa połowie liczby psów.
D) 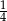 liczby psów.
liczby psów.
E) 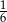 liczby psów.
liczby psów.
Pole trójkąta przedstawionego na rysunku jest równe 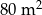 , a promień każdego okręgu w środku w jego wierzchołku jest równy 2 m. Ile metrów kwadratowych ma pole zacieniowanej figury?
, a promień każdego okręgu w środku w jego wierzchołku jest równy 2 m. Ile metrów kwadratowych ma pole zacieniowanej figury?
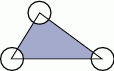
A) 76 B) 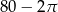 C)
C) 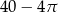 D)
D) 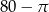 E)
E) 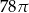
W miejsce znaku zapytania wpisz brakujące cyfry, by spełniona była podana równość:
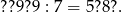
W miejsce znaku zapytania wpisz brakujące cyfry, by spełniona była podana równość:
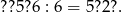
W miejsce znaku zapytania wpisz brakujące cyfry, by spełniona była podana równość.
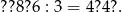
W miejsce znaku zapytania wpisz brakujące cyfry, by spełniona była podana równość:
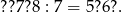
Dany jest trójkąt 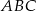 , w którym
, w którym 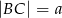 . Z wierzchołka
. Z wierzchołka 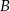 poprowadzono środkową
poprowadzono środkową 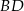 do boku
do boku 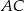 . Punkt
. Punkt 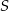 jest środkiem odcinka
jest środkiem odcinka 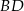 . Przez punkty
. Przez punkty 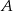 i
i 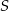 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 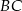 w punkcie
w punkcie 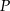 . Wykaż, że długość odcinka
. Wykaż, że długość odcinka 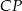 jest równa
jest równa 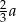 .
.
Dany jest trójkąt 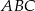 oraz punkt
oraz punkt  na jego boku
na jego boku 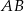 taki, że
taki, że 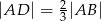 . Z wierzchołka
. Z wierzchołka 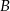 poprowadzono środkową
poprowadzono środkową 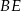 do boku
do boku 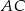 . Punkt
. Punkt 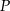 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 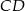 i
i 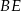 . Wykaż, że punkt
. Wykaż, że punkt 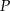 jest środkiem odcinka
jest środkiem odcinka 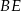 .
.
Z jabłek, śliwek, pomarańczy i bananów układamy na półce kompozycje, kładąc kolejno owoc za owocem. Kompozycja jest kompletna, gdy bezpośrednio za owocem dowolnego rodzaju przynajmniej raz leży owoc każdego innego rodzaju. Z ilu owoców składa się najmniej liczna kompletna kompozycja owoców?
A) 13 B) 8 C) 16 D) 4 E) 12
Odcinek 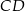 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 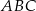 , w którym
, w którym 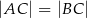 . Punkt
. Punkt 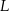 jest rzutem punktu
jest rzutem punktu 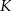 wysokości
wysokości 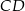 na bok
na bok 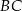 . Udowodnij, że
. Udowodnij, że 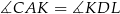 .
.
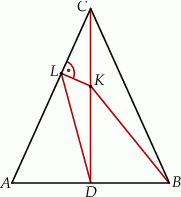
Odcinek  jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego  , w którym
, w którym  . Punkt
. Punkt 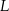 jest rzutem punktu
jest rzutem punktu 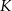 wysokości
wysokości 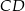 na bok
na bok 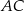 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 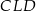 jest podobny do trójkąta
jest podobny do trójkąta 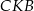 .
.
Na rysunku obok, trójkąt i kwadrat mają równe obwody. Ile wynosi obwód całej figury (pięciokąta)?
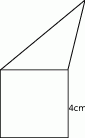
A) 12 cm B) 24 cm C) 28 cm D) 32 cm E) 20 cm
Na kartce napisano w jednej linii kilka różnych liczb całkowitych dodatnich nie większych niż 10. Oglądając tę kartkę, Mirek stwierdził ze zdumieniem, że w każdej parze sąsiednich liczb jedna z nich dzieli drugą. Ile co najwyżej liczb mogło byc napisanych na tej kartce?
A) 6 B) 7 C) 8 D) 9 E) 10
Okrąg przecina boki prostokąta 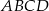 w punktach
w punktach 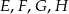 , jak na rysunku obok. Wiadomo, że
, jak na rysunku obok. Wiadomo, że 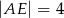 ,
, 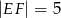 ,
, 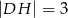 . Ile wynosi długość odcinka
. Ile wynosi długość odcinka 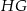 ?
?
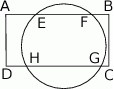
A) 6 B) 7 C) 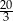 D) 8 E) 9
D) 8 E) 9
Klasa liczy 9 chłopców i 13 dziewcząt. Połowa uczniów tej klasy jest przeziębiona. Co najmniej ile dziewcząt jest przeziębionych?
A) 0 B) 1 C) 2 D) 3 E) 4
Nauczyciel zadał maturzystom serię zadań, które mieli rozwiązać w określonym terminie. Karol postanowił codziennie rozwiązywać tę samą liczbę zadań. Krzysiek obliczył, że jeśli dziennie będzie rozwiązywał o 2 zadania więcej od Karola, to skończy o 3 dni wcześniej niż Karol. Maciek postanowił rozwiązywać codziennie o 2 zadania więcej od Krzyśka i obliczył, że wszystkie zadania rozwiąże o 2 dni wcześniej niż Krzysiek. Ile zadań mieli do rozwiązania maturzyści?
Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych jest równa sumie długości średnic okręgów wpisanego i opisanego na tym trójkącie.
Przyprostokątne trójkąta prostokątnego mają długości  i
i 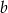 , a jego przeciwprostokątna ma długość
, a jego przeciwprostokątna ma długość  . Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość
. Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość 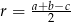 .
.
Wewnątrz kąta o mierze 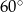 leży punkt
leży punkt 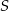 . Odległość tego punktu od ramion kąta wynosi odpowiednio
. Odległość tego punktu od ramion kąta wynosi odpowiednio 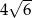 i
i 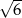 . Oblicz odległość tego punktu od wierzchołka kąta.
. Oblicz odległość tego punktu od wierzchołka kąta.

