Napisz wzór funkcji kwadratowej w postaci ogólnej wiedząc, że funkcja ma jedno miejsce zerowe oraz do jej wykresu należą punkty 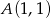 oraz
oraz 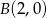 .
.
/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu
Parabola, która jest wykresem funkcji kwadratowej  , ma z osiami kartezjańskiego układu współrzędnych
, ma z osiami kartezjańskiego układu współrzędnych 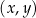 dokładnie dwa punkty wspólne:
dokładnie dwa punkty wspólne: 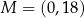 oraz
oraz 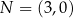 . Wyznacz wzór funkcji kwadratowej
. Wyznacz wzór funkcji kwadratowej 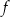 .
.
Pewna parabola o wierzchołku 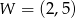 przecina oś
przecina oś 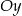 w punkcie
w punkcie 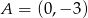 .
.
- Wyznacz postać ogólną funkcji kwadratowej
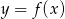 , której wykresem jest ta parabola.
, której wykresem jest ta parabola. - Rozwiąż nierówność
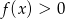 .
.
Wykres funkcji kwadratowej 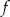 określonej wzorem
określonej wzorem 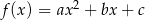 ma z prostą o równaniu
ma z prostą o równaniu 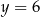 dokładnie jeden punkt wspólny. Punkty
dokładnie jeden punkt wspólny. Punkty 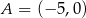 i
i 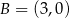 należą do wykresu funkcji
należą do wykresu funkcji 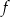 . Oblicz wartości współczynników
. Oblicz wartości współczynników 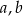 oraz
oraz  .
.
Funkcja 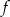 określona jest wzorem
określona jest wzorem 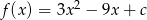 , gdzie
, gdzie 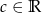 . Wyznacz wszystkie wartości współczynnika
. Wyznacz wszystkie wartości współczynnika  , dla których:
, dla których:
- jednym z miejsc zerowych funkcji
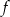 jest liczba 2;
jest liczba 2; - wierzchołek paraboli, która jest wykresem funkcji
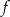 , należy do prostej o równaniu
, należy do prostej o równaniu 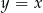 .
.
Wykresem funkcji 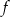 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 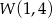 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 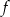 w przedziale
w przedziale 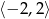 wynosi -5.
wynosi -5.
- Przedstaw wzór funkcji
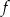 w postaci iloczynowej.
w postaci iloczynowej. - Rozwiąż nierówność
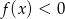 .
.
Dana jest funkcja 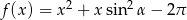 , dla
, dla 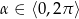 .
.
- Wyznacz wszystkie wartości parametru
 , dla których osią symetrii wykresu tej funkcji jest prosta
, dla których osią symetrii wykresu tej funkcji jest prosta 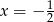 .
. - Wykaż, że nie istnieje taka wartość parametru
 , dla której do wykresu funkcji
, dla której do wykresu funkcji 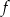 należy punkt
należy punkt 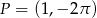 .
.
Wykresem funkcji kwadratowej 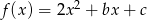 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 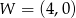 . Oblicz wartości współczynników
. Oblicz wartości współczynników 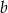 i
i  .
.
Wykresem funkcji kwadratowej 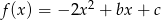 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 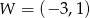 . Oblicz wartości współczynników
. Oblicz wartości współczynników 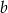 i
i  .
.
Wyznacz współczynniki  i
i 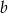 funkcji kwadratowej
funkcji kwadratowej 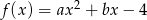 , jeśli współrzędne wierzchołka wynoszą
, jeśli współrzędne wierzchołka wynoszą 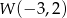 . Przedstaw trójmian w postaci iloczynowej.
. Przedstaw trójmian w postaci iloczynowej.
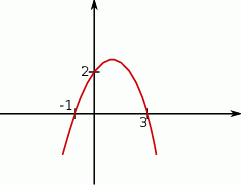
Na podstawie wykresu funkcji kwadratowej podaj jej wzór w postaci ogólnej, kanonicznej oraz iloczynowej.