Proste 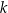 i
i 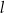 przecinają się w punkcie
przecinają się w punkcie 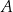 . Proste
. Proste 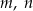 i
i  są wzajemnie równoległe i przecinają obie proste
są wzajemnie równoległe i przecinają obie proste 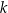 i
i 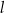 w punktach
w punktach 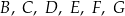 (zobacz rysunek poniżej), w taki sposób, że:
(zobacz rysunek poniżej), w taki sposób, że: 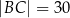 ,
, 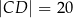 ,
, 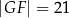 .
.
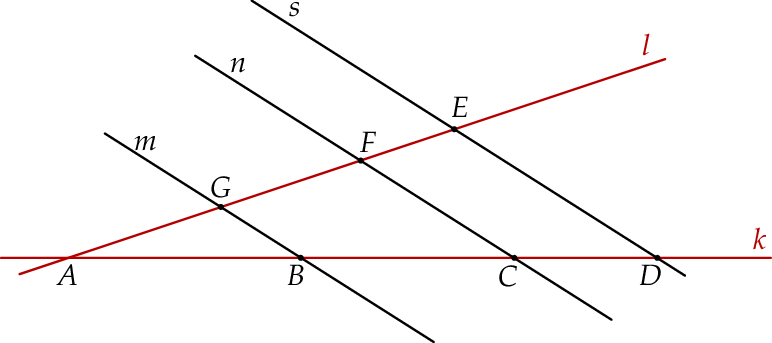
Oblicz długość odcinka 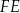 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Proste 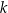 i
i 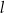 przecinają się w punkcie
przecinają się w punkcie 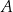 . Proste
. Proste 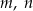 i
i  są wzajemnie równoległe i przecinają obie proste
są wzajemnie równoległe i przecinają obie proste 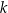 i
i 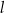 w punktach
w punktach 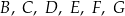 (zobacz rysunek poniżej), w taki sposób, że:
(zobacz rysunek poniżej), w taki sposób, że: 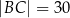 ,
, 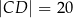 ,
, 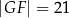 .
.

Oblicz długość odcinka 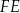 .
.
Podstawą ostrosłupa jest trójkąt prostokątny o kącie ostrym  i przeciwprostokątnej długości
i przeciwprostokątnej długości  . Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem
. Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 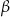 . Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe
. Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe 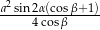 .
.
Punkty 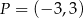 ,
, 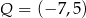 i
i 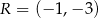 są środkami odpowiednio boków
są środkami odpowiednio boków 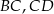 i
i 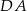 równoległoboku
równoległoboku 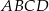 . Wyznacz współrzędne wierzchołków tego równoległoboku.
. Wyznacz współrzędne wierzchołków tego równoległoboku.
Pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego o krawędzi podstawy  wyraża się wzorem
wyraża się wzorem 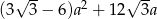 . Wyznacz sumę długości krawędzi podstawy i wysokości tego graniastosłupa.
. Wyznacz sumę długości krawędzi podstawy i wysokości tego graniastosłupa.
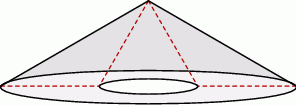
Trójkąt równoramienny o kącie 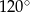 i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.
i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.
Wierzchołkami kwadratu 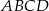 są punkty o współrzędnych
są punkty o współrzędnych 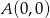 ,
, 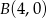 ,
, 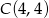 i
i 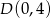 . Dla każdej liczby rzczywistej
. Dla każdej liczby rzczywistej 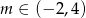 rozważamy trójkąt o wierzchołkach
rozważamy trójkąt o wierzchołkach 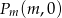 ,
, 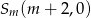 i
i 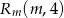 . Wyznacz wszystkie wartości prametru
. Wyznacz wszystkie wartości prametru 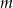 , dla których pole figury, która jest częścią wspólną kwadratu
, dla których pole figury, która jest częścią wspólną kwadratu 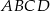 i trójkąta
i trójkąta 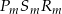 wynosi 2.
wynosi 2.
Dany jest prostokąt 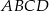 . Okręgi o średnicach
. Okręgi o średnicach 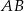 i
i 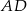 przecinają się w punktach
przecinają się w punktach 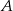 i
i 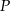 .
.
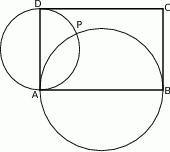
Wykaż, że punkty 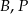 i
i 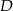 leżą na jednej prostej.
leżą na jednej prostej.
Punkty 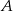 i
i 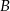 są punktami wspólnymi dwóch okręgów, a odcinki
są punktami wspólnymi dwóch okręgów, a odcinki 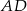 i
i 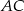 ich średnicami.
ich średnicami.
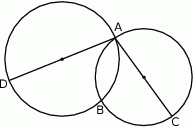
Wykaż, że punkt 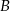 leży na prostej przechodzącej przez punkty
leży na prostej przechodzącej przez punkty 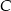 i
i 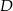 .
.
Dany jest równoległobok 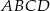 . Okręgi o średnicach
. Okręgi o średnicach 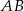 i
i 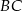 przecinają się w punktach
przecinają się w punktach 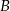 i
i 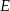 .
.
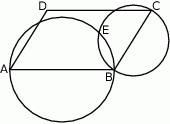
Wykaż, że punkty 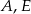 i
i 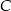 leżą na jednej prostej.
leżą na jednej prostej.
Wyznacz równanie takiej prostej przechodzącej przez punkt 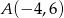 , która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
, która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest półkolem. Oblicz miarę kąta rozwarcia stożka.
Graniastosłup prawidłowy czworokątny przecięto płaszczyzną, która zawiera krawędź podstawy oraz przechodzi przez środek przeciwległej krawędzi bocznej (zobacz rysunek).
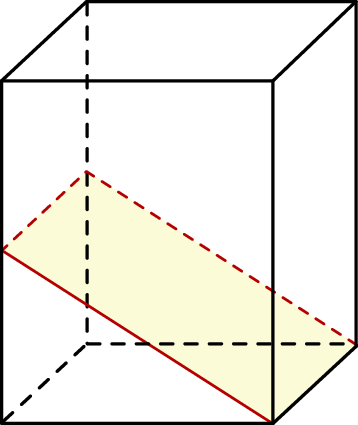
Oblicz jaki jest stosunek objętości dwóch brył na jakie został podzielony ten graniastosłup.
Przekrój osiowy stożka jest trójkątem równobocznym o polu 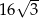 . Oblicz objętość i pole powierzchni całkowitej tego stożka.
. Oblicz objętość i pole powierzchni całkowitej tego stożka.
W okrąg o promieniu 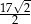 wpisano czworokąt
wpisano czworokąt 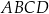 tak, że
tak, że 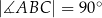 oraz
oraz 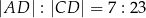 . Oblicz obwód czworokąta
. Oblicz obwód czworokąta 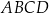 jeżeli jego pole jest równe 192.
jeżeli jego pole jest równe 192.
Środki ścian sześcianu są wierzchołkami innej bryły – ośmiościanu foremnego (zobacz rysunek).
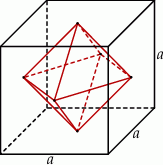
Oblicz objętość tego ośmiościanu jeżeli krawędź sześcianu ma długość  .
.
Wykaż, że wysokość 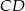 trójkąta prostokątnego
trójkąta prostokątnego 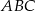 poprowadzona z wierzchołka
poprowadzona z wierzchołka 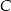 kąta prostego dzieli przeciwprostokątną na odcinki
kąta prostego dzieli przeciwprostokątną na odcinki 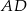 i
i 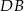 , których stosunek długości jest równy stosunkowi kwadratów długości przyprostokątnych odpowiednio
, których stosunek długości jest równy stosunkowi kwadratów długości przyprostokątnych odpowiednio 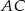 i
i 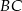 tego trójkąta.
tego trójkąta.
Na okręgu o promieniu 1 opisano trójkąt prostokątny, którego przyprostokątne mają długości  i
i 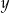 .
.
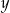 jako funkcję
jako funkcję  i określ dziedzinę tej funkcji.
i określ dziedzinę tej funkcji. Pole powierzchni bocznej stożka jest czterokrotnie większe od pola podstawy stożka. Oblicz wysokość stożka, wiedząc, że promień jego podstawy jest równy  .
.
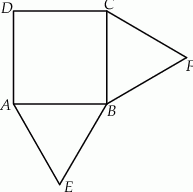
Na zewnątrz kwadratu 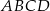 na bokach
na bokach 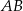 i
i 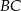 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 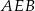 i
i 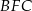 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 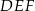 jest równoboczny.
jest równoboczny.
Długość ramienia trapezu jest równa 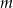 , a odległość od niego środka przeciwległego ramienia jest równa
, a odległość od niego środka przeciwległego ramienia jest równa 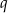 . Wyznacz pole trapezu.
. Wyznacz pole trapezu.
W kole o promieniu 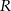 poprowadzono średnicę
poprowadzono średnicę 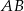 i równoległą do niej cięciwę
i równoległą do niej cięciwę 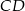 . Oblicz pole powstałego trapezu
. Oblicz pole powstałego trapezu 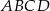 , jeżeli kąt ostry tego trapezu ma miarę
, jeżeli kąt ostry tego trapezu ma miarę  .
.
Różnica kwadratów długości przekątnych trapezu prostokątnego wynosi 21, jego wysokość ma długość 4, a dłuższe ramię ma długość 5. Oblicz pole trapezu.
