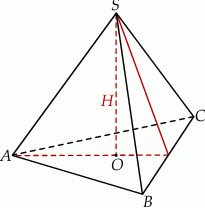
Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 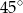 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
/Szkoła średnia/Geometria
Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 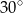 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
Podstawą ostrosłupa jest trójkąt prostokątny, którego kąt ostry ma miarę 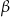 . Wszystkie krawędzie boczne mają długość
. Wszystkie krawędzie boczne mają długość 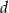 i są nachylone do płaszczyzny podstawy pod kątem o mierze
i są nachylone do płaszczyzny podstawy pod kątem o mierze  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W czworościanie, którego wszystkie krawędzie mają taką samą długość 6, umieszczono kulę tak, że ma ona dokładnie jeden punkt wspólny z każdą ścianą czworościanu. Płaszczyzna 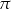 , równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości równej
, równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości równej 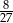 objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka
objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka 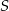 kuli od płaszczyzny
kuli od płaszczyzny 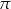 , tj. długość najkrótszego spośród odcinków
, tj. długość najkrótszego spośród odcinków 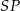 , gdzie
, gdzie 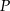 jest punktem płaszczyzny
jest punktem płaszczyzny 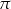 .
.
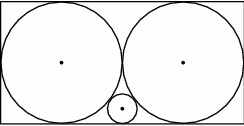
W prostokąt wpisano trzy parami styczne okręgi w ten sposób, że dwa z nich są styczne do trzech boków, prostokąta, a trzeci jest styczny do jednego z boków prostokąta (patrz rysunek). Oblicz promień mniejszego okręgu jeżeli promień większego okręgu jest równy 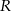 .
.
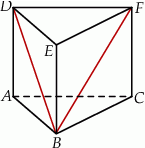
Podstawą graniastosłupa prostego 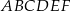 jest trójkąt
jest trójkąt 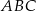 , w którym
, w którym 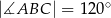 oraz
oraz 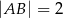 (zobacz rysunek). Trójkąt
(zobacz rysunek). Trójkąt 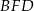 jest równoboczny. Oblicz pole powierzchni całkowitej tego graniastosłupa.
jest równoboczny. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Dana jest prosta 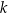 o równaniu
o równaniu 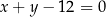 oraz punkt
oraz punkt 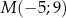 wyznacz na prostej
wyznacz na prostej 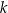 takie punkty
takie punkty 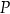 i
i 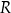 aby
aby 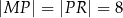 .
.
Liczby 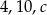 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Liczby 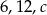 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Liczby 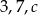 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Przekątne czworokąta 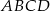 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 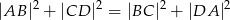 .
.
Znajdź zbiór środków wszystkich okręgów stycznych wewnętrznie do okręgu o równaniu 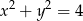 i stycznych do prostej o równaniu
i stycznych do prostej o równaniu 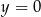 .
.
Dany jest czworokąt wypukły 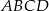 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 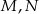 są odpowiednio środkami boków
są odpowiednio środkami boków 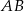 i
i 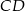 . Punkty
. Punkty 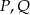 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 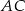 i
i 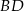 . Uzasadnij, że
. Uzasadnij, że 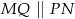 .
.
Dany jest czworokąt wypukły 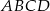 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 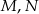 są odpowiednio środkami boków
są odpowiednio środkami boków 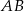 i
i 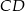 . Punkty
. Punkty 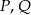 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 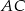 i
i 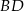 . Uzasadnij, że czworokąt
. Uzasadnij, że czworokąt 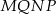 jest równoległobokiem.
jest równoległobokiem.
W prostokącie 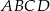 , w którym stosunek długości boków
, w którym stosunek długości boków 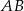 i
i 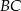 jest równy 4:3, poprowadzono dwusieczne kątów
jest równy 4:3, poprowadzono dwusieczne kątów 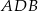 i
i 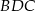 . Dwusieczne te przecinają boki
. Dwusieczne te przecinają boki 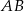 i
i 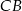 odpowiednio w punktach
odpowiednio w punktach 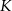 i
i 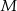 . Oblicz stosunek pola prostokąta
. Oblicz stosunek pola prostokąta 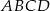 do pola trójkąta
do pola trójkąta 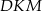 .
.
W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość 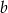 , a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę
, a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Wszystkie wierzchołki czworokąta 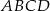 leżą na okręgu oraz
leżą na okręgu oraz 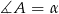 . Oblicz miarę kąta
. Oblicz miarę kąta  .
.
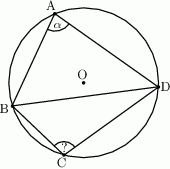
Punkty 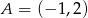 i
i 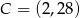 są wierzchołkami trójkąta równoramiennego, w którym
są wierzchołkami trójkąta równoramiennego, w którym 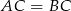 . Prosta zawierająca wysokość opuszczoną z wierzchołka
. Prosta zawierająca wysokość opuszczoną z wierzchołka 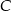 ma równanie
ma równanie 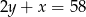 . Oblicz pole trójkąta
. Oblicz pole trójkąta 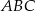 .
.
Dany jest trójkąt prostokątny 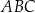 , w którym
, w którym 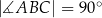 oraz
oraz 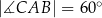 . Punkty
. Punkty 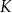 i
i 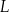 leżą na bokach – odpowiednio –
leżą na bokach – odpowiednio – 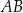 i
i 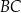 tak, że
tak, że 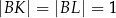 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 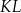 przecina wysokość
przecina wysokość 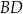 tego trójkąta w punkcie
tego trójkąta w punkcie 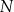 , a ponadto
, a ponadto 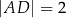 .
.
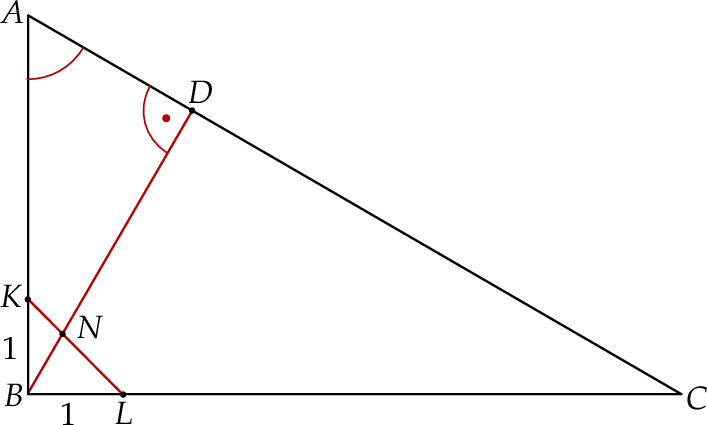
Wykaż, że 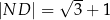 .
.
Odcinki 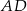 i
i 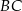 przecinają się w punkcie
przecinają się w punkcie 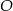 . W trójkątach
. W trójkątach 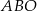 i
i 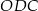 zachodzą związki:
zachodzą związki: 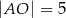 ,
, 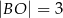 ,
, 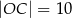 ,
, 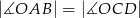 (zobacz rysunek).
(zobacz rysunek).
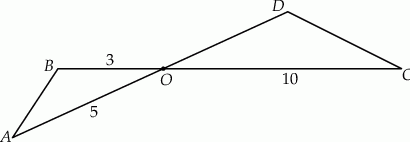
Oblicz długość boku 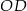 trójkąta
trójkąta 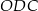 .
.
Odcinki 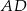 i
i 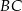 przecinają się w punkcie
przecinają się w punkcie 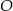 . W trójkątach
. W trójkątach 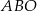 i
i 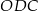 zachodzą związki:
zachodzą związki: 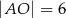 ,
, 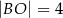 ,
, 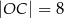 ,
, 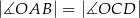 (zobacz rysunek).
(zobacz rysunek).
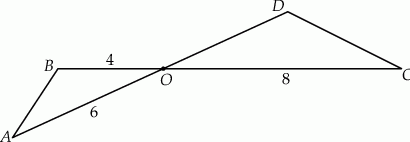
Oblicz długość boku 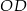 trójkąta
trójkąta 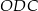 .
.
Na rysunku przedstawiono fragment siatki graniastosłupa prawidłowego trójkątnego.
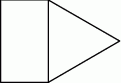
Pole narysowanego trójkąta jest równe 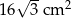 , a pole prostokąta jest równe
, a pole prostokąta jest równe 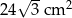 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 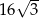 , a jego objętość
, a jego objętość 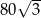 . Wyznacz cosinus kąta
. Wyznacz cosinus kąta  nachylenia ściany bocznej do płaszczyzny podstawy.
nachylenia ściany bocznej do płaszczyzny podstawy.
Podstawą graniastosłupa prostego 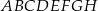 jest romb o boku długości 5, polu 24 i kącie ostrym
jest romb o boku długości 5, polu 24 i kącie ostrym 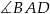 . Graniastosłup ten przecięto płaszczyzną
. Graniastosłup ten przecięto płaszczyzną 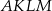 w ten sposób, że otrzymany przekrój jest rombem o kącie ostrym
w ten sposób, że otrzymany przekrój jest rombem o kącie ostrym 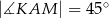 (zobacz rysunek). Oblicz pole tego przekroju.
(zobacz rysunek). Oblicz pole tego przekroju.
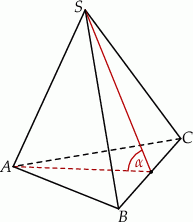
Objętość ostrosłupa prawidłowego trójkątnego 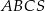 (tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę
(tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę 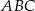 tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.
tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.
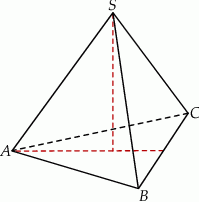
Objętość ostrosłupa prawidłowego trójkątnego 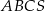 (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie
(patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie 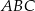 tego ostrosłupa jest równy 2. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
tego ostrosłupa jest równy 2. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
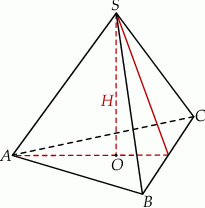
Objętość ostrosłupa prawidłowego trójkątnego 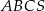 (tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę
(tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę 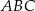 tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną.
tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną.
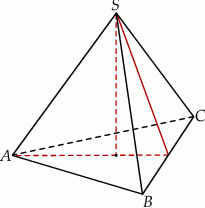
Objętość ostrosłupa prawidłowego trójkątnego 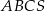 (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie
(patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie 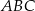 tego ostrosłupa jest równy 4. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
tego ostrosłupa jest równy 4. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.