Dany jest trójkąt o wymiarach 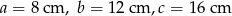 . Oblicz obwód trójkąta podobnego w skali 5.
. Oblicz obwód trójkąta podobnego w skali 5.
/Szkoła średnia/Geometria
Dany jest trójkąt o wymiarach 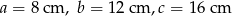 . Oblicz obwód trójkąta podobnego w skali
. Oblicz obwód trójkąta podobnego w skali 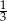 .
.
Oblicz objętość i pole powierzchni graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 6 cm i 8 cm, którego przekątna ściany bocznej tworzy z krawędzią podstawy kąt o mierze 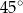 .
.
Wspólne styczne dwóch okręgów stycznych zewnętrznie przecinają się pod kątem 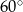 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.
Do dwóch stycznych zewnętrznie okręgów poprowadzono dwie wspólne styczne: jedną zewnętrzną i jedną wewnętrzną. Proste te przecinają się pod kątem 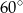 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.
Znajdź równanie okręgu stycznego do prostej 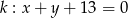 i do prostej
i do prostej 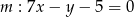 w punkcie
w punkcie 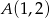 .
.
Ramię trapezu równoramiennego 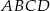 ma długość
ma długość 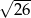 . Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
Dla dowolnej liczby 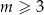 , prosta
, prosta 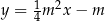 przecina hiperbolę
przecina hiperbolę 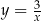 w punktach
w punktach 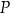 i
i 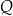 . Uzasadnij, że
. Uzasadnij, że 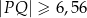 .
.
Dany jest prostokąt o polu 12, w którym długość przekątnej jest liczbą z przedziału 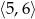 . Wykaż, że obwód tego prostokąta jest liczbą z przedziału
. Wykaż, że obwód tego prostokąta jest liczbą z przedziału 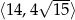 .
.
Na bokach 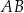 i
i 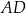 rombu
rombu 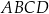 wybrano odpowiednio punkty
wybrano odpowiednio punkty 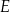 i
i 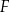 tak, że
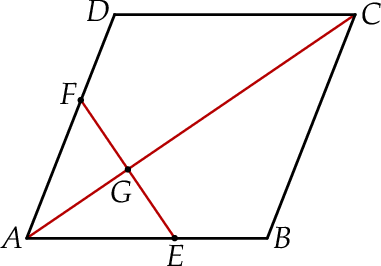
tak, że 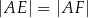 . Pole pięciokąta
. Pole pięciokąta 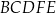 jest 17 razy większe niż pole trójkąta
jest 17 razy większe niż pole trójkąta 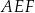 . Punkt
. Punkt 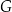 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 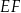 i przekątnej
i przekątnej 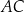 . Oblicz Oblicz
. Oblicz Oblicz 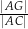 .
.
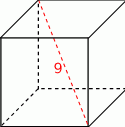
Przekątna sześcianu ma długość 9. Oblicz pole powierzchni całkowitej tego sześcianu.
Na bokach 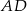 ,
, 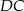 i
i 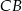 kwadratu
kwadratu 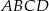 wybrano punkty
wybrano punkty 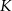 ,
, 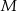 i
i 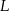 ten sposób, że
ten sposób, że 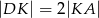 ,
, 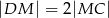 , oraz
, oraz 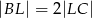 .
.
- Uzasadnij, że trójkąt
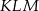 jest prostokątny.
jest prostokątny. - Oblicz tangensy kątów ostrych trójkąta
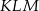 .
.
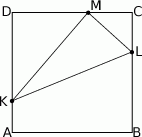
Określ wzajemne położenie prostych 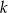 i
i 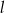 o równaniach
o równaniach
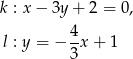
Na bokach 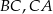 i
i 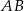 trójkąta
trójkąta 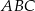 wybrano punkty
wybrano punkty 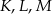 takie, że
takie, że
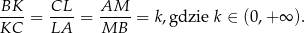
Wyznacz wartość 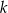 , dla której stosunek pola trójkąta
, dla której stosunek pola trójkąta 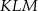 do pola trójkąta
do pola trójkąta 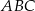 jest najmniejszy.
jest najmniejszy.
Pole rombu jest równe 120. Gdyby zwiększyć długości jego przekątnych odpowiednio o 2 i 5 to pole wzrosłoby o 55. Oblicz obwód rombu. Podaj wszystkie możliwe odpowiedzi.
W trójkącie równobocznym 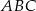 połączono środki wysokości otrzymując trójkąt
połączono środki wysokości otrzymując trójkąt 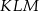 . Oblicz stosunek pól trójkątów
. Oblicz stosunek pól trójkątów 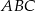 i
i 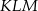 .
.
Współrzędne przeciwległych wierzchołków prostokąta 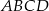 są równe
są równe 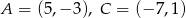 . Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek
. Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek 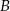 leży na prostej
leży na prostej 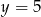 .
.
Wykaż, że w sześcianie, odległość krawędzi od nieprzecinającej się z nią przekątnej sześcianu jest równa połowie długości przekątnej ściany.
Przez środek jednej krawędzi podstawy sześcianu, koniec przeciwległej krawędzi tej podstawy oraz środek krawędzi bocznej, poprowadzono płaszczyznę. Opisz figurę, którą otrzymamy w wyniku tego przekroju. Rozważ 2 przypadki.
Prosta o równaniu 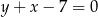 zawiera jedną z dwusiecznych kątów wewnętrznych trójkąta
zawiera jedną z dwusiecznych kątów wewnętrznych trójkąta 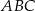 , w którym
, w którym 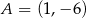 i
i 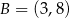 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Suma długości krawędzi graniastosłupa prawidłowego czworokątnego jest równa 16. Dla jakiej długości krawędzi podstawy pole powierzchni całkowitej tego graniastosłupa będzie największe?
Suma krawędzi graniastosłupa prawidłowego trójkątnego jest równa 3. Dla jakiej długości krawędzi podstawy pole powierzchni całkowitej tego graniastosłupa będzie największe?
Dane są punkty 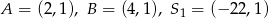 i
i 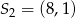 . Odcinek
. Odcinek 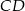 jest obrazem odcinka
jest obrazem odcinka 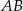 w jednokładności o skali dodatniej i środku
w jednokładności o skali dodatniej i środku 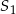 , jak i w jednokładności o skali ujemnej i środku
, jak i w jednokładności o skali ujemnej i środku 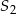 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 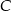 i
i  .
.

