Dany jest trójkąt równoboczny 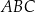 , w którym
, w którym 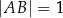 . Na boku
. Na boku 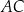 tego trójkąta wybrano taki punkt
tego trójkąta wybrano taki punkt 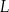 , że
, że 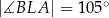 . Odcinek
. Odcinek 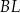 przecina wysokość
przecina wysokość 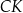 trójkąta
trójkąta 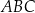 w punkcie
w punkcie 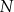 (zobacz rysunek).
(zobacz rysunek).
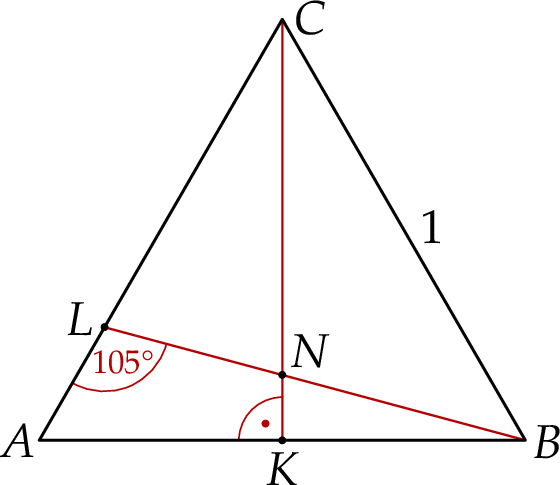
Oblicz długość odcinka 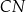 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trójkąt równoboczny 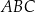 , w którym
, w którym 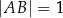 . Na boku
. Na boku 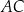 tego trójkąta wybrano taki punkt
tego trójkąta wybrano taki punkt 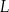 , że
, że 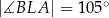 . Odcinek
. Odcinek 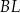 przecina wysokość
przecina wysokość 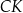 trójkąta
trójkąta 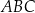 w punkcie
w punkcie 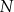 (zobacz rysunek).
(zobacz rysunek).

Oblicz długość odcinka 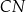 .
.
Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości  . Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Jakie powinny być długości pozostałych krawędzi graniastosłupa, aby jego objętość była największa?
. Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Jakie powinny być długości pozostałych krawędzi graniastosłupa, aby jego objętość była największa?
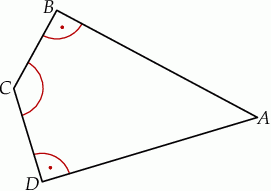
W czworokącie wypukłym 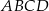 (zobacz rysunek poniżej) dane są kąty:
(zobacz rysunek poniżej) dane są kąty: 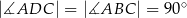 oraz
oraz 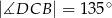 . Wykaż, że
. Wykaż, że 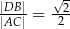 .
.
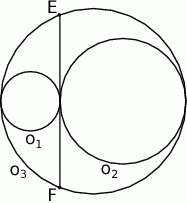
Dane są trzy okręgi 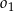 ,
, 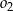 i
i 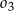 . Okręgi
. Okręgi 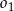 ,
, 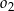 są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu
są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu 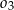 (patrz rysunek). Promienie okręgów
(patrz rysunek). Promienie okręgów 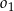 i
i 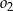 są odpowiednio równe
są odpowiednio równe 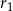 i
i 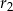 , a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka
, a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka 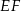 jest równa
jest równa 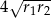 , gdzie odcinek
, gdzie odcinek 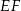 jest cięciwą okręgu
jest cięciwą okręgu 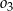 i zawiera się we wspólnej stycznej okręgów
i zawiera się we wspólnej stycznej okręgów 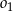 i
i 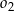 .
.
Mrówka przeszła po powierzchni sześcianu z wierzchołka 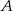 do wierzchołka będącego drugim końcem przekątnej sześcianu wychodzącej z wierzchołka
do wierzchołka będącego drugim końcem przekątnej sześcianu wychodzącej z wierzchołka 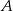 , przy czym była to droga najkrótsza. Narysuj siatkę sześcianu i oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość
, przy czym była to droga najkrótsza. Narysuj siatkę sześcianu i oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość 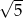 .
.
Dany jest ostrosłup prawidłowy czworokątny o krawędzi bocznej dwa razy dłuższej od krawędzi podstawy.
Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa.
Wyznacz długość krawędzi ostrosłupa, tak aby pole jego powierzchni bocznej wynosiło 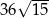 .
.
Udowodnij, że jeżeli punkt 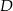 jest środkiem ciężkości trójkąta, to
jest środkiem ciężkości trójkąta, to 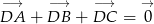 .
.
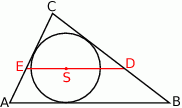
Przez środek 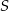 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 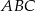 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 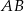 , która przecina boki
, która przecina boki 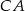 i
i 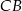 odpowiednio w punktach
odpowiednio w punktach 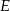 i
i 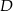 .
.
Wykaż, że 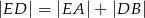 .
.
Dane są dwa przeciwległe wierzchołki kwadratu 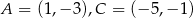 . Wyznacz obwód tego kwadratu.
. Wyznacz obwód tego kwadratu.
Dane są dwa przeciwległe wierzchołki kwadratu 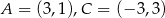 . Oblicz obwód tego kwadratu.
. Oblicz obwód tego kwadratu.
Na bokach 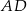 i
i 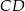 kwadratu
kwadratu 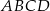 o boku długości 1 wybrano punkty
o boku długości 1 wybrano punkty 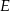 i
i 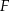 w ten sposób, że
w ten sposób, że 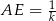 i
i 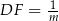 , dla
, dla 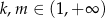 . Niech
. Niech 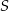 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków 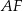 i
i 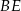
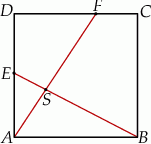
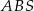 jest prostokątny to
jest prostokątny to 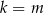 .
. 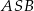 jeżeli
jeżeli 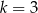 i
i 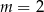 .
.Wyznacz wartości funkcji trygonometrycznych kąta 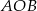 oraz jego miarę, jeżeli
oraz jego miarę, jeżeli 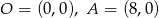 oraz
oraz
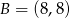
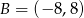
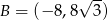
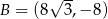
Dany jest trapez prostokątny 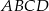 o podstawach
o podstawach 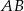 i
i 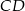 , w którym boki
, w którym boki 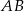 i
i 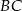 są prostopadłe. Dwusieczne kątów
są prostopadłe. Dwusieczne kątów 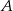 i
i 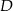 przecinają się w punkcie
przecinają się w punkcie 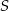 leżącym na boku
leżącym na boku 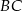 . Wykaż, że
. Wykaż, że 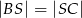 .
.
Punkty 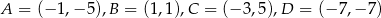 są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
Punkty 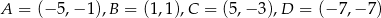 są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
Dany jest sześcian 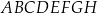 o krawędzi długości
o krawędzi długości  . Punkt
. Punkt 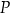 jest środkiem krawędzi
jest środkiem krawędzi 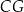 tego sześcianu.
tego sześcianu.
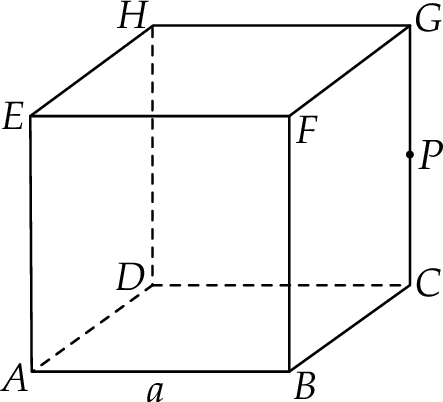
Oblicz odległość wierzchołka 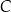 od płaszczyzny zawierającej punkty
od płaszczyzny zawierającej punkty 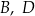 oraz
oraz 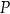 .
.
W okręgu o promieniu 5 poprowadzono dwie równoległe cięciwy o długościach 6 i 8. Oblicz odległość między tymi cięciwami.
Podstawą ostrosłupa prawidłowego 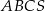 jest trójkąt równoboczny
jest trójkąt równoboczny 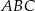 o boku długości 6. Na krawędziach bocznych
o boku długości 6. Na krawędziach bocznych 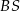 i
i 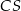 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 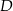 i
i 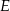 , takie że
, takie że 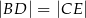 oraz
oraz 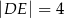 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 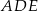 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 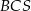 ostrosłupa.
ostrosłupa.
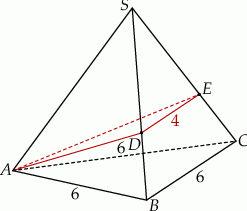
Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa prawidłowego  jest trójkąt równoboczny
jest trójkąt równoboczny  o boku długości 8. Na krawędziach bocznych
o boku długości 8. Na krawędziach bocznych  i
i 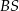 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 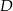 i
i 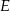 , takie że
, takie że 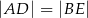 oraz
oraz 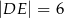 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 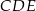 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 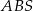 ostrosłupa.
ostrosłupa.
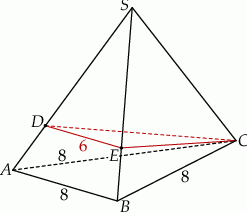
Oblicz objętość tego ostrosłupa.
Podstawą prostopadłościanu jest prostokąt o stosunku boków 1:3. Objętość bryły jest równa 12. Oblicz wymiary tego prostopadłościanu, aby jego powierzchnia całkowita była najmniejsza. Oblicz tę najmniejszą powierzchnię.
Podstawą ostrosłupa jest prostokąt, którego stosunek długości boków wynosi 2:3. Pole podstawy ostrosłupa jest równe 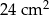 . Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem
. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 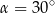 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Podstawą ostrosłupa jest prostokąt, którego stosunek długości boków wynosi 4:3. Pole podstawy ostrosłupa jest równe 48. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 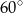 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Dany jest pięciokąt foremny 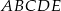 o boku długości
o boku długości  . Wiedząc, że
. Wiedząc, że 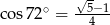
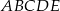 jest równa
jest równa 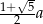 ;
; 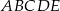 .
.Punkty 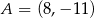 i
i 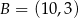 są końcami cięciwy okręgu o środku
są końcami cięciwy okręgu o środku 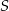 . Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt
. Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt 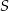 .
.
