Dla jakich wartości parametru 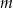 równanie
równanie 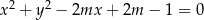 opisuje okrąg?
opisuje okrąg?
- Podaj współrzędne środka i długość promienia okręgu.
- Dla jakich wartości parametru
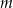 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 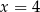 ?
?
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dla jakich wartości parametru 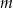 równanie
równanie 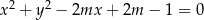 opisuje okrąg?
opisuje okrąg?
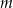 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 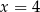 ?
?Podstawą ostrosłupa 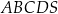 jest kwadrat
jest kwadrat 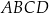 (patrz rysunek).
(patrz rysunek).
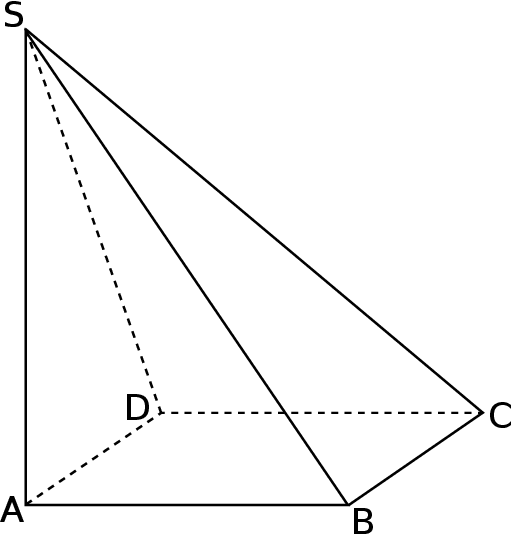
Krawędź 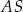 jest wysokością tego ostrosłupa. Odległość punktu
jest wysokością tego ostrosłupa. Odległość punktu 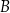 od krawędzi
od krawędzi 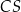 jest równa
jest równa 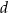 , a kąt dwuścienny między ścianami
, a kąt dwuścienny między ścianami 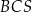 i
i 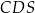 ma miarę
ma miarę 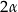 , gdzie
, gdzie 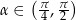 . Oblicz:
. Oblicz:
odległość punktu 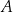 od krawędzi
od krawędzi 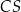
wysokość tego ostrosłupa.
W ostrosłupie 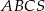 podstawa
podstawa 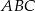 jest trójkątem prostokątnym,
jest trójkątem prostokątnym, 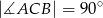 . Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość
. Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość 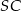 ostrosłupa ma długość 24 cm. Oblicz:
ostrosłupa ma długość 24 cm. Oblicz:
Przez punkt 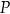 krawędzi bocznej
krawędzi bocznej 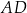 graniastosłupa prawidłowego trójkątnego
graniastosłupa prawidłowego trójkątnego 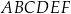 o krawędzi podstawy równej
o krawędzi podstawy równej  poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem
poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem  , a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem
, a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem 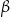 (zobacz rysunek).
(zobacz rysunek).
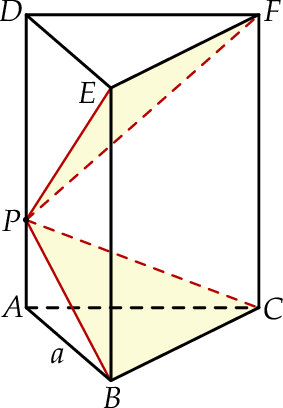
Udowodnij, że objętość ostrosłupa 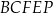 jest równa
jest równa
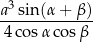
Obwód trójkąta prostokątnego wynosi 60 cm, a tangens jednego z kątów ostrych jest równy 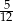 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
Obwód trójkąta prostokątnego wynosi 72 cm, a tangens jednego z kątów ostrych jest równy 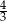 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
Po wydłużeniu każdej krawędzi sześcianu o 2, długość jego przekątnej podwoiła się. Oblicz pole powierzchni całkowitej powiększonego sześcianu.
Trzy różne punkty 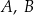 i
i 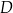 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 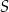 . Odcinek
. Odcinek 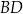 jest średnicą tego okręgu. Styczne
jest średnicą tego okręgu. Styczne 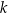 i
i 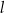 do tego okręgu, odpowiednio w punktach
do tego okręgu, odpowiednio w punktach 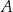 i
i 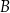 , przecinają się w punkcie
, przecinają się w punkcie 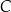 (zobacz rysunek poniżej).
(zobacz rysunek poniżej).

Wykaż, że trójkąty 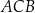 i
i 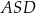 są podobne.
są podobne.
Odległość wierzchołka sześcianu od przekątnej sześcianu (do której dany wierzchołek nie należy) jest równa 4 cm. Oblicz objętość sześcianu.
Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 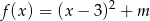 , gdzie
, gdzie 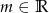 – parametr.
– parametr.
Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 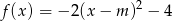 , gdzie
, gdzie 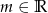 – parametr.
– parametr.
Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 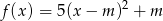 , gdzie
, gdzie 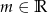 – parametr.
– parametr.
Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 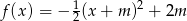 , gdzie
, gdzie 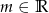 – parametr.
– parametr.
Na rysunku przedstawiono bryłę, której podstawą jest kwadrat a ściany boczne są prostopadłe do płaszczyzny podstawy. Wymiary bryły podane są na rysunku.
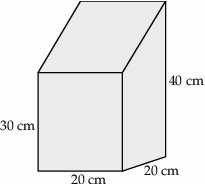
Oblicz objętość tej bryły.
W trójkącie 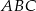 , gdzie
, gdzie 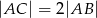 dane są
dane są 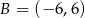 i
i 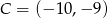 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 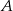 , jeżeli leży on na prostej
, jeżeli leży on na prostej 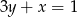 .
.
Na bokach 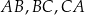 trójkąta równobocznego
trójkąta równobocznego 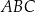 wybrano kolejno punkty
wybrano kolejno punkty 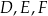 tak, że
tak, że 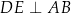 ,
, 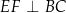 i
i 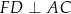 .
.

Wykaż, że trójkąt 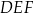 jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta
jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta 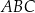 .
.
Podstawą ostrosłupa jest romb, którego przekątne mają długości 12 i 16. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych rombu w podstawie, a pole powierzchni bocznej jest równe 104. Oblicz objętość ostrosłupa.
Okrąg przecina boki czworokąta 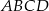 kolejno w punktach
kolejno w punktach 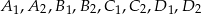 (zobacz rysunek).
(zobacz rysunek).
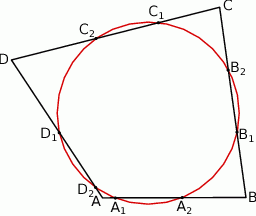
Wykaż, że jeżeli 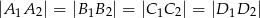 , to w czworokąt
, to w czworokąt 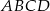 można wpisać okrąg.
można wpisać okrąg.
W kartezjańskim układzie współrzędnych 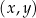 dane są punkty
dane są punkty 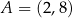 oraz
oraz 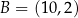 . Symetralna odcinka
. Symetralna odcinka 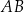 przecina oś
przecina oś 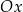 układu współrzędnych w punkcie
układu współrzędnych w punkcie 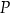 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 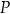 oraz długość odcinka
oraz długość odcinka 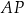 .
.
W trójkącie 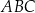 dane są długości dwóch boków
dane są długości dwóch boków 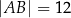 ,
, 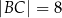 oraz miara kąta
oraz miara kąta 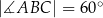 . Oblicz długość środkowej tego trójkąta poprowadzonej z wierzchołka A.
. Oblicz długość środkowej tego trójkąta poprowadzonej z wierzchołka A.
Dany jest trójkąt prostokątny o polu 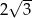 i kącie ostrym
i kącie ostrym 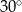 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny o polu 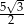 i kącie ostrym
i kącie ostrym  . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny o polu 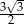 i kącie ostrym
i kącie ostrym 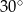 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Liczba przekątnych wielokąta wypukłego, w którym jest  boków i
boków i 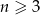 wyraża się wzorem
wyraża się wzorem 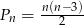 .
.
Kąt ostry między przekątnymi równoległoboku 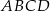 ma miarę
ma miarę 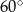 . Przekątna
. Przekątna 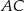 ma długość 6, a przekątna
ma długość 6, a przekątna 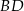 jest prostopadła do boku
jest prostopadła do boku 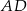 . Oblicz długości boków równoległoboku.
. Oblicz długości boków równoległoboku.
Punkty 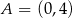 i
i 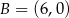 są końcami odcinka
są końcami odcinka 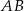 . Prosta
. Prosta 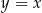 przecina odcinek
przecina odcinek 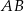 w punkcie
w punkcie 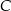 . Oblicz stosunek
. Oblicz stosunek 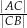 .
.
Punkty 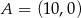 i
i 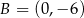 są końcami odcinka
są końcami odcinka 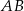 . Prosta
. Prosta 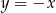 przecina odcinek
przecina odcinek 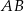 w punkcie
w punkcie 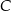 . Oblicz stosunek
. Oblicz stosunek 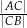 .
.
