Stosując zasadę indukcji matematycznej, wykaż, że dla każdej liczby całkowitej 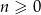 zachodzi równość
zachodzi równość
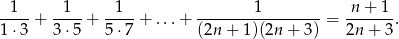
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Stosując zasadę indukcji matematycznej, wykaż, że dla każdej liczby całkowitej 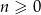 zachodzi równość
zachodzi równość
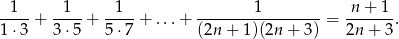
Pokazać, że dla każdej liczby naturalnej  liczba
liczba 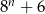 jest podzielna przez 7.
jest podzielna przez 7.
Stosując zasadę indukcji matematycznej, wykaż, że dla każdej liczby naturalnej dodatniej  zachodzi równość
zachodzi równość
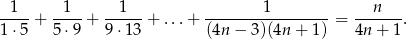
Uzasadnij wzór
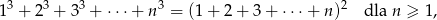
a następnie
