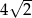Liczbą odwrotną do liczby 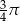 jest liczba:
jest liczba:
A) 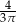 B)
B) 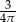 C)
C) 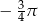 D)
D) 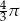
/Szkoła średnia/Zadania testowe/Liczby
Liczba 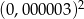 jest równa
jest równa
A) 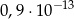 B)
B) 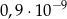 C)
C) 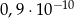 D)
D) 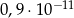
Liczba 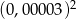 jest równa
jest równa
A) 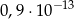 B)
B) 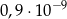 C)
C) 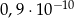 D)
D) 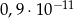
Liczba 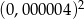 jest równa
jest równa
A) 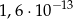 B)
B) 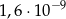 C)
C) 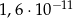 D)
D) 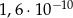
Wyrażenie 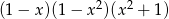 jest równe
jest równe
A) 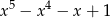 B)
B) 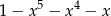 C)
C) 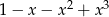 D)
D) 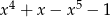
Liczby rzeczywiste  i
i 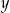 są dodatnie. Wyrażenie
są dodatnie. Wyrażenie 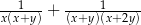 można przekształcić do postaci
można przekształcić do postaci
A) 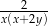 B)
B) 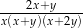 C)
C) 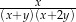 D)
D) 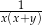
Liczba  jest odwrotnością liczby
jest odwrotnością liczby 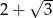 , zaś
, zaś 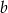 jest liczbą przeciwną do liczby
jest liczbą przeciwną do liczby 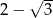 . Różnica
. Różnica 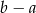 jest wówczas równa:
jest wówczas równa:
A) 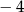 B)
B) 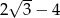 C)
C) 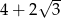 D) 0
D) 0
Liczba 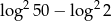 jest równa
jest równa
A) 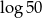 B)
B) 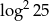 C)
C) 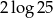 D)
D) 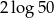
Liczba 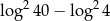 jest równa
jest równa
A) 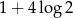 B)
B) 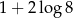 C)
C) 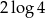 D)
D) 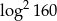
Liczba 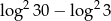 jest równa
jest równa
A) 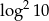 B)
B) 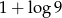 C)
C) 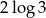 D)
D) 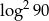
Liczba 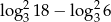 jest równa
jest równa
A) 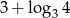 B)
B) 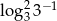 C)
C) 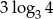 D)
D) 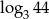
Liczba 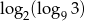 jest równa
jest równa
A) 1 B) 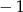 C) 2 D)
C) 2 D) 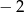
Liczba 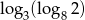 jest równa
jest równa
A) 1 B) 2 C) 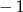 D)
D) 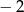
Liczba 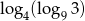 jest równa
jest równa
A) 1 B) 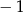 C)
C) 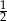 D)
D) 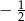
Przybliżenie dziesiętne liczby 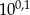 z dokładnością do pięciu miejsc po przecinku jest równe 1,25893. Przybliżeniem dziesiętnym liczby
z dokładnością do pięciu miejsc po przecinku jest równe 1,25893. Przybliżeniem dziesiętnym liczby 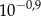 z dokładnością do 0,001 jest liczba
z dokładnością do 0,001 jest liczba
A) 0,126 B) 1,259 C) 12,589 D) 7,943
Przybliżenie dziesiętne liczby 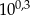 z dokładnością do czterech miejsc po przecinku jest równe 1,9953. Przybliżeniem dziesiętnym liczby
z dokładnością do czterech miejsc po przecinku jest równe 1,9953. Przybliżeniem dziesiętnym liczby 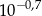 z dokładnością do 0,01 jest liczba
z dokładnością do 0,01 jest liczba
A) 0,02 B) 19,95 C) 0,19 D) 0,2
Przybliżenie dziesiętne liczby 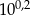 z dokładnością do pięciu miejsc po przecinku jest równe 1,58489. Przybliżeniem dziesiętnym liczby
z dokładnością do pięciu miejsc po przecinku jest równe 1,58489. Przybliżeniem dziesiętnym liczby 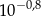 z dokładnością do 0,001 jest liczba
z dokładnością do 0,001 jest liczba
A) 1,1585 B) 0,158 C) 15,849 D) 0,159
Przybliżenie dziesiętne liczby 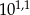 z dokładnością do pięciu miejsc po przecinku jest równe 12,58925. Przybliżeniem dziesiętnym liczby
z dokładnością do pięciu miejsc po przecinku jest równe 12,58925. Przybliżeniem dziesiętnym liczby 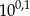 z dokładnością do 0,001 jest liczba
z dokładnością do 0,001 jest liczba
A) 0,126 B) 1,259 C) 125,892 D) 7,943
Przybliżenie liczby 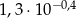 jest równe 0,5175393. Przybliżeniem liczby
jest równe 0,5175393. Przybliżeniem liczby 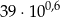 z dokładnością do 3 miejsca po przecinku jest liczba
z dokładnością do 3 miejsca po przecinku jest liczba
A) 15,526 B) 1552,618 C) 155,262 D) 1552,617
Przybliżenie liczby 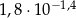 jest równe 0,07165929. Przybliżeniem liczby
jest równe 0,07165929. Przybliżeniem liczby 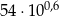 z dokładnością do 3 miejsca po przecinku jest liczba
z dokładnością do 3 miejsca po przecinku jest liczba
A) 21,499 B) 214,978 C) 2149,779 D) 71,659
O liczbie  wiadomo, że
wiadomo, że 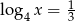 . Zatem
. Zatem
A) 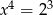 B)
B) 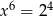 C)
C) 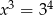 D)
D) 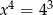
O liczbie  wiadomo, że
wiadomo, że 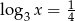 . Zatem
. Zatem
A) 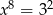 B)
B) 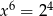 C)
C) 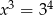 D)
D) 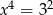
Dla każdej dodatniej liczby  iloraz
iloraz 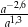 jest równy
jest równy
A) 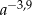 B)
B) 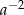 C)
C) 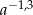 D)
D) 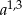
Dla każdej dodatniej liczby  iloraz
iloraz 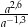 jest równy
jest równy
A) 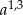 B)
B) 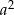 C)
C) 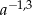 D)
D) 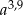
Liczba 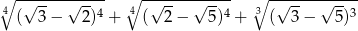 jest równa
jest równa
A) 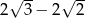 B)
B) 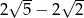 C)
C) 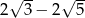 D)
D) 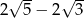
Liczba 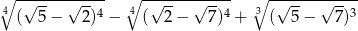 jest równa
jest równa
A) 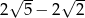 B)
B) 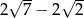 C)
C) 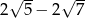 D)
D) 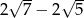
Liczba 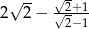 jest liczbą
jest liczbą
A) wymierną B) niewymierną C) większą niż 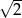 D) naturalną
D) naturalną
Liczba 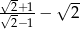 jest liczbą
jest liczbą
A) wymierną B) niewymierną C) mniejszą niż 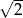 D) naturalną
D) naturalną
Wyrażenie 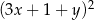 jest równe
jest równe
A) 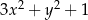 B)
B) 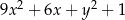
C) 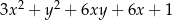 D)
D) 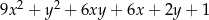
Wyrażenie 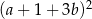 jest równe
jest równe
A) 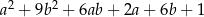 B)
B) 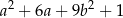
C) 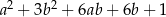 D)
D) 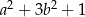
W rozwinięciu dziesiętnym ułamka 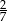 na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Liczbę 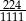 można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Dwudziestą cyfrą po przecinku jego rozwinięcia jest
można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Dwudziestą cyfrą po przecinku jego rozwinięcia jest
A) 2 B) 0 C) 1 D) 6
W rozwinięciu dziesiętnym ułamka 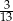 na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 6 B) 9 C) 2 D) 3
W rozwinięciu dziesiętnym ułamka 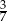 na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Liczbę 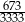 można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Trzydziestą cyfrą po przecinku jego rozwinięcia jest
można zapisać w postaci nieskończonego ułamka dziesiętnego okresowego. Trzydziestą cyfrą po przecinku jego rozwinięcia jest
A) 2 B) 0 C) 1 D) 9
W rozwinięciu dziesiętnym ułamka 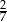 na czterdziestym miejscu po przecinku stoi cyfra
na czterdziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 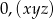 . Wiemy, że cyfra znajdująca się na 22 miejscu po przecinku tego rozwinięcia jest równa 7, cyfra znajdująca się na miejscu 26 jest równa 3, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 22 miejscu po przecinku tego rozwinięcia jest równa 7, cyfra znajdująca się na miejscu 26 jest równa 3, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka  jest więc równy
jest więc równy
A) 732 B) 273 C) 244 D) 723
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 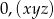 . Wiemy, że cyfra znajdująca się na 16 miejscu po przecinku tego rozwinięcia jest równa 2, cyfra znajdująca się na miejscu 23 jest równa 3, a cyfra znajdująca się na miejscu 18 jest równa 7. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 16 miejscu po przecinku tego rozwinięcia jest równa 2, cyfra znajdująca się na miejscu 23 jest równa 3, a cyfra znajdująca się na miejscu 18 jest równa 7. Licznik ułamka  jest więc równy
jest więc równy
A) 79 B) 273 C) 237 D) 244
Rozwinięcie dziesiętne nieskracalnego ułamka zwykłego  jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci
jest ułamkiem dziesiętnym okresowym, który można zapisać w postaci 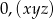 . Wiemy, że cyfra znajdująca się na 19 miejscu po przecinku tego rozwinięcia jest równa 3, cyfra znajdująca się na miejscu 26 jest równa 7, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka
. Wiemy, że cyfra znajdująca się na 19 miejscu po przecinku tego rozwinięcia jest równa 3, cyfra znajdująca się na miejscu 26 jest równa 7, a cyfra znajdująca się na miejscu 15 jest równa 2. Licznik ułamka  jest więc równy
jest więc równy
A) 372 B) 273 C) 244 D) 124
Liczba 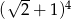 jest większa od liczby
jest większa od liczby 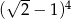 o
o
A) 2 B) 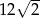 C)
C) 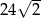 D)
D)