Średnia arytmetyczna zestawu danych: 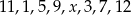 o medianie 7,5 jest równa
o medianie 7,5 jest równa
A) 8 B) 7,5 C) 7 D) 6,75
/Szkoła średnia/Zadania testowe/Statystyka
Średnia arytmetyczna zestawu danych: 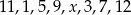 o medianie 6,5 jest równa
o medianie 6,5 jest równa
A) 8 B) 7,5 C) 7 D) 6,75
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
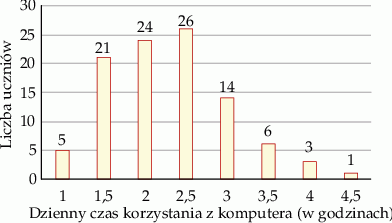
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Mediana dziennego czasu korzystania przez ucznia z komputera jest równa 2,25 godziny. | P | F |
| Połowa z tej grupy uczniów korzysta dziennie z komputera przez mniej niż 2,5 godziny. | P | F |
Na diagramie przedstawiono oceny z pracy klasowej z matematyki w klasie IIa.
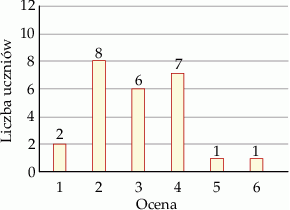
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dominanta ocen otrzymanych z pracy klasowej jest mniejsza od 3. | P | F |
| Mediana ocen otrzymanych z pracy klasowej jest równa 3,5. | P | F |
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
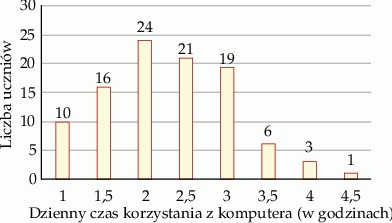
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Mediana dziennego czasu korzystania przez ucznia z komputera jest równa 2 godziny. | P | F |
| Połowa z tej grupy uczniów korzysta dziennie z komputera przez więcej niż 2 godziny. | P | F |
W grupie 50 kobiet i 50 mężczyzn przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba książek | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 23 | 14 | 28 | 17 | 11 | 7 |
W trakcie analizy tych danych zauważono, że kobiety przeczytały średnio o jedną książkę więcej niż mężczyźni. Średnia liczba przeczytanych książek przez jednego ankietowanego mężczyznę jest równa
A) 1,5 B) 1 C) 2 D) 2,5
W grupie 50 kobiet i 50 mężczyzn przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba książek | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 19 | 21 | 24 | 21 | 7 | 8 |
W trakcie analizy tych danych zauważono, że kobiety przeczytały średnio o dwie książki więcej niż mężczyźni. Średnia liczba przeczytanych książek przez jednego ankietowanego mężczyznę jest równa
A) 1,5 B) 1 C) 2 D) 2,5
W grupie 50 kobiet i 50 mężczyzn przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba książek | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 23 | 14 | 28 | 17 | 11 | 7 |
W trakcie analizy tych danych zauważono, że kobiety przeczytały średnio o jedną książkę więcej niż mężczyźni. Średnia liczba przeczytanych książek przez jedną ankietowaną kobietę jest równa
A) 1,5 B) 1 C) 2 D) 2,5
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 3 | 6 | 8 | 4 | 4 | 2 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 0,2 B)  C)
C) 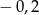 D)
D) 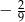
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 2 | 4 | 7 | 2 | 3 | 2 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 0,3 B) 3,3 C) 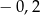 D) 3
D) 3
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 5 | 3 | 5 | 7 | 3 | 1 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 3,125 B) 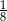 C) 1,125 D)
C) 1,125 D) 
W grupie 320 respondentów przeprowadzono ankietę, w której zapytano o liczbę wysłanych przez nich wiadomości e-mail pomiędzy 1 a 6 marca. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba e-maili | 10 | 20 | 30 | 40 | 50 | 60 |
| Liczba osób | 53 | 93 | 28 | 75 | 44 | 27 |
A) 5 B) 10 C) 4 D) 6
Jacek planując wycieczkę zagraniczną postanowił ocenić kilka ofert przyznając punkty w trzech kategoriach
| Nr oferty | Cena | Atrakcyjność | Dostępność |
| I | 1 | 3 | 4 |
| II | 2 | 2 | 2 |
| III | 3 | 1 | 2 |
Aby porównać ze sobą oferty postanowił policzyć średnią ważoną przyznanych punktów stosując następujące wagi:
| Kategoria | Cena | Atrakcyjność | Dostępność |
| Waga | 50 | 35 | 15 |
Wycieczki, dla których policzona średnia jest najwyższa to
A) I i II B) II i III C) I i III D) III
Średnia arytmetyczna liczb: 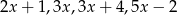 i
i 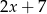 zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 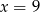 B)
B) 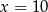 C)
C) 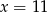 D)
D) 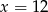
Średnia arytmetyczna liczb: 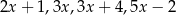 i
i 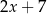 zmniejsza się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zmniejsza się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 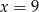 B)
B) 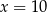 C)
C) 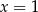 D)
D) 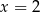
Średnia arytmetyczna liczb: 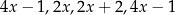 i
i 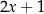 zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 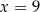 B)
B) 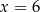 C)
C) 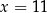 D)
D) 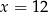
Mediana uporządkowanego niemalejąco zestawu liczb: 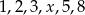 nie zmienia się po dopisaniu liczby 10. Wtedy
nie zmienia się po dopisaniu liczby 10. Wtedy
A) 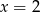 B)
B) 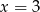 C)
C) 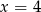 D)
D) 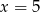
W grupie 320 respondentów przeprowadzono ankietę, w której zapytano o liczbę wysłanych przez nich wiadomości e-mail pomiędzy 1 a 6 marca. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba e-maili | 10 | 20 | 30 | 40 | 50 | 60 |
| Liczba osób | 53 | 93 | 28 | 75 | 44 | 27 |
A) 20 B) 25 C) 30 D) 35
Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach.
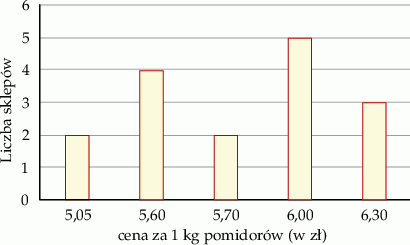
Mediana ceny kilograma pomidorów w tych wybranych sklepach jest równa
A) 5,80 zł B) 5,73 zł C) 5,85 zł D) 6,00 zł E) 5,70 zł
Na diagramie poniżej przedstawiono ceny ogórków w szesnastu wybranych sklepach.
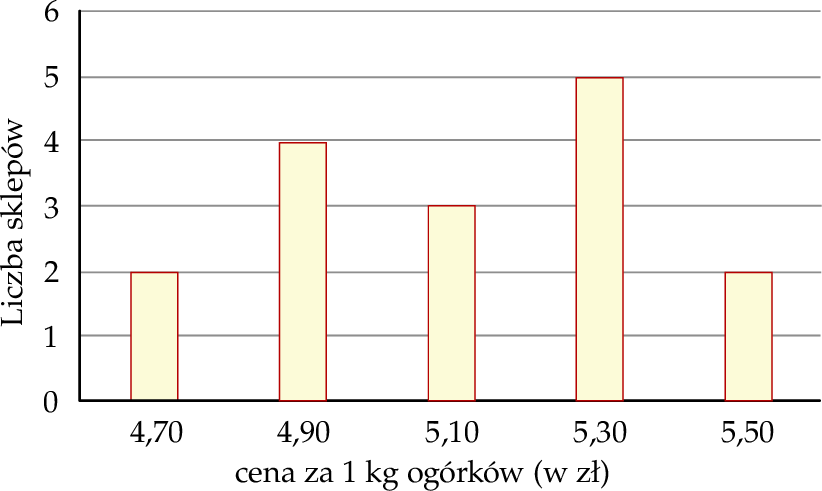
Mediana ceny kilograma ogórków w tych wybranych sklepach jest równa
A) 4,80 zł B) 4,90 zł C) 5,00 zł D) 5,10 zł E) 5,20 zł
Na diagramie poniżej przedstawiono ceny 1 kostki masła (200 g) w stu wybranych sklepach.
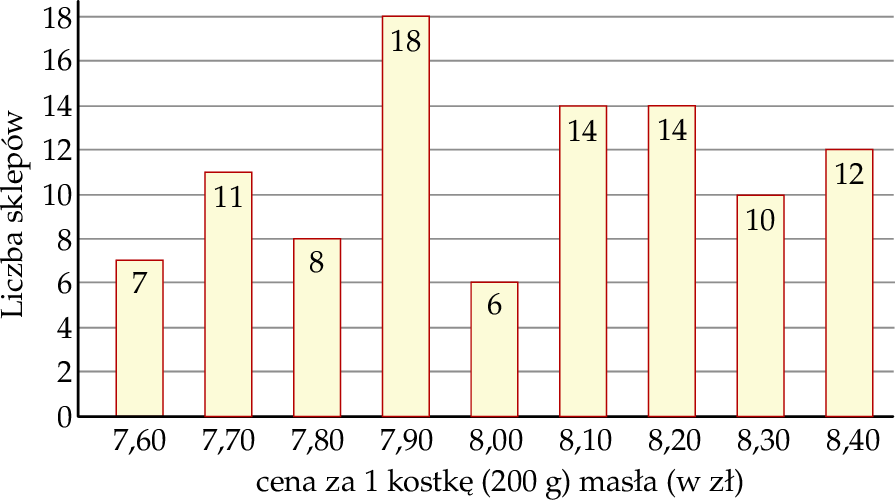
Mediana ceny 1 kostki masła w tych wybranych sklepach jest równa
A) 8,00 zł B) 7,95 zł C) 7,90 zł D) 8,10 zł E) 8,05 zł
W pewnej klasie, w której jest dwa razy więcej dziewczynek niż chłopców, średnia wzrostu wszystkich chłopców jest równa 157 cm, a średnia wzrostu wszystkich dziewczynek jest równa 160 cm. Średni wzrost uczniów tej klasy jest równy
A) 158 cm B) 158,5 cm C) 159 cm D) 159,5 cm
Średnia arytmetyczna liczby punktów uzyskanych na egzaminie przez studentów I grupy, liczącej 40 studentów, jest równa 30. Dwudziestu studentów tworzących II grupę otrzymało w sumie 1800 punktów. Zatem średni wynik z tego egzaminu, liczony łącznie dla wszystkich studentów z obu grup, jest równy
A) 20 pkt B) 30 pkt C) 50 pkt D) 60 pkt
Średnia arytmetyczna danych z tabelki
| Wartość danej | -6 | 6 | -9 | 9 |
| Liczebność danej | 2 | 4 | 1 | 3 |
wynosi
A) 3 B) 0 C) -3 D) 1
W tabeli zestawiono liczbę punktów uzyskanych przez 32 uczniów pewnej klasy za rozwiązanie jednego z zadań testu z matematyki.
| Liczba punktów | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba uczniów | 2 | 2 | 5 | 6 | 11 | 6 |
Średnia arytmetyczna liczby punktów uzyskanych za rozwiązanie tego zadania przez uczniów tej klasy jest równa
A) 2,5 B) 3,25 C) 3,31 D) 4
W tabeli poniżej przedstawione są wyniki pracy klasowej.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba ocen | 3 | 7 | 6 | 9 | 2 | 0 |
Średnia ocen w tej klasie jest równa
A) 3 B) 3,5 C) 4 D) 5
Średnia arytmetyczna danych z tabelki
| Wartość danej | -6 | -9 | 6 | 9 |
| Liczebność danej | 4 | 2 | 1 | 3 |
wynosi
A) 7,5 B) -0,9 C) 0 D) 0,8
Średnia arytmetyczna danych z tabelki
| Wartość danej | -3 | 6 | -9 | 5 |
| Liczebność danej | 3 | 4 | 1 | 2 |
wynosi
A) 1,6 B) -0,1 C) -1 D) 2
Wojtek notował temperaturę powietrza o godzinie 12.00 w pięciu kolejnych dniach stycznia. Otrzymał następujące wyniki:
| Data | 15.01 | 16.01 | 17.01 | 18.01 | 19.01 |
| Temperatura | 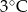 | 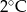 | 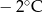 | 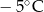 | 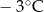 |
Odchylenie standardowe od średniej temperatury w tych dniach, z dokładnością do 0,1 wynosi
A) 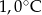 B)
B) 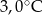 C)
C) 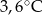 D)
D) 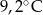
Na diagramie przedstawiono oceny z pracy klasowej z matematyki w klasie IIa.
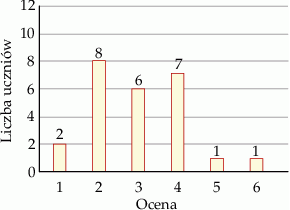
Odchylenie standardowe danych przedstawionych na diagramie jest równe
A) 1,2 B) 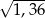 C)
C) 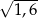 D) 1,6
D) 1,6
Jeżeli do zestawu czterech danych: 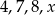 dołączymy liczbę 2, to średnia arytmetyczna wzrośnie o 2. Zatem
dołączymy liczbę 2, to średnia arytmetyczna wzrośnie o 2. Zatem
A) 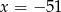 B)
B) 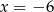 C)
C) 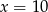 D)
D) 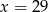
Jeżeli do zestawu czterech danych: 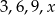 dołączymy liczbę 3, to średnia arytmetyczna wzrośnie o 2. Zatem
dołączymy liczbę 3, to średnia arytmetyczna wzrośnie o 2. Zatem
A) 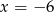 B)
B) 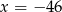 C)
C) 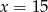 D)
D) 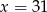
Średnia ważona danych z tabeli
| Wartość danej | 4 | 5 | 6 | 8 |
| Waga | 4 | 3 | 1 | 2 |
jest równa
A) 2,3 B) 5,75 C) 5,3 D) 14,5
Średnia ważona danych z tabeli
| Wartość danej | 3 | 4 | 5 | 7 |
| Waga | 2 | 1 | 4 | 3 |
jest równa
A) 4,5 B) 4,75 C) 5,3 D) 5,1
Średnia ważona danych z tabeli
| Wartość danej | 3 | 5 | 7 | 8 |
| Waga | 1 | 3 | 4 | 2 |
jest równa
A) 12,4 B) 6,2 C) 5,7 D) 5,75
Dla zestawu liczb: 1, 3, 2, 4, 3
A) mediana jest równa 2 i średnia arytmetyczna jest równa 2,6.
B) mediana jest równa 3 i średnia arytmetyczna jest równa 3.
C) mediana jest równa 2 i średnia arytmetyczna jest równa 3.
D) mediana jest równa 3 i średnia arytmetyczna jest równa 2,6.
Średnia arytmetyczna czterech liczb: 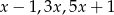 i
i 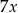 jest równa 72. Wynika stąd, że
jest równa 72. Wynika stąd, że
A) 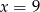 B)
B) 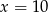 C)
C) 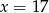 D)
D) 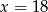
Średnia arytmetyczna czterech liczb dodatnich: 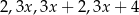 jest równa
jest równa 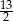 . Wynika stąd, że
. Wynika stąd, że
A) 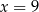 B)
B) 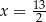 C)
C) 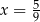 D)
D) 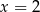
Średnia arytmetyczna pięciu liczb: 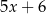 ,
, 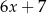 ,
, 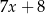 ,
, 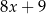 ,
, 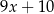 , jest równa 8. Wtedy
, jest równa 8. Wtedy  jest równe
jest równe
A) 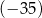 B) 0 C) 0,35 D) 35
B) 0 C) 0,35 D) 35
Średnia arytmetyczna czterech liczb dodatnich: 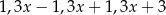 jest równa
jest równa 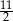 . Wynika stąd, że
. Wynika stąd, że
A) 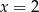 B)
B) 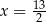 C)
C) 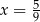 D)
D) 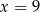
Średnia arytmetyczna pięciu liczb: 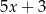 ,
, 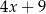 ,
, 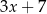 ,
, 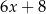 ,
, 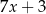 , jest równa 11. Wtedy
, jest równa 11. Wtedy  jest równe
jest równe
A) 1 B) 5 C) 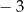 D)
D) 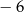
Średnia arytmetyczna czterech liczb: 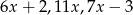 i
i 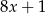 jest równa 88. Wynika stąd, że
jest równa 88. Wynika stąd, że
A) 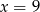 B)
B) 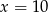 C)
C) 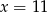 D)
D) 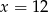
Średnia arytmetyczna zestawu danych: 2, 4, 7, 8, 9 jest taka sama jak średnia arytmetyczna zestawu danych: 2, 4, 7, 8, 9,  . Wynika stąd, że
. Wynika stąd, że
A) 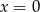 B)
B) 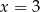 C)
C) 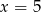 D)
D) 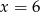
Średnia arytmetyczna zestawu danych: 3, 5, 6, 7, 9 jest taka sama jak średnia arytmetyczna zestawu danych: 3, 5, 6, 8, 9,  . Wynika stąd, że
. Wynika stąd, że
A) 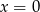 B)
B) 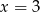 C)
C) 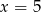 D)
D) 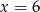
Średnia arytmetyczna zestawu liczb 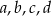 jest równa 20. Wtedy średnia arytmetyczna zestawu liczb
jest równa 20. Wtedy średnia arytmetyczna zestawu liczb 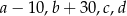 jest równa
jest równa
A) 10 B) 20 C) 25 D) 30
Średnia arytmetyczna liczb 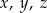 jest równa 4. Średnia arytmetyczna czterech liczb:
jest równa 4. Średnia arytmetyczna czterech liczb:
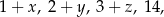
jest równa
A) 6 B) 9 C) 8 D) 13
Średnia arytmetyczna trzech liczb: 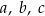 , jest równa 9. Średnia arytmetyczna sześciu liczb:
, jest równa 9. Średnia arytmetyczna sześciu liczb: 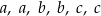 , jest równa
, jest równa
A) 9 B) 6 C) 4,5 D) 18

