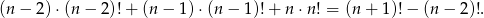W urnie jest 7 kul czarnych i 5 białych. Sześć z nich przekładamy do drugiej urny, początkowo pustej, i z niej losujemy 2 kule bez zwracania. Jakie jest prawdopodobieństwo, że druga z nich będzie biała.
/Szkoła średnia
Rysunek przedstawia wykres funkcji 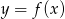 .
.
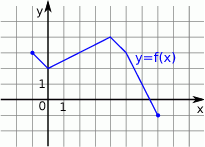
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 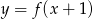 .
.
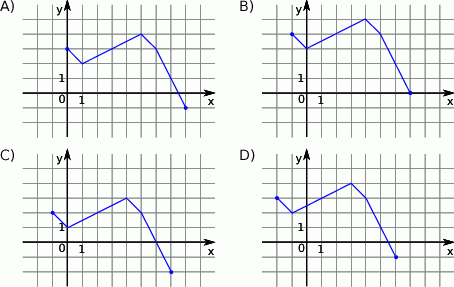
Rysunek przedstawia wykres funkcji 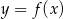 .
.
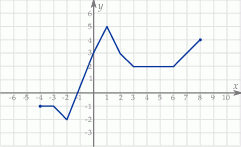
Wskaż wykres funkcji 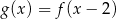 .
.
Na rysunku dany jest wykres funkcji 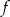 .
.
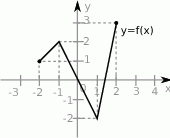
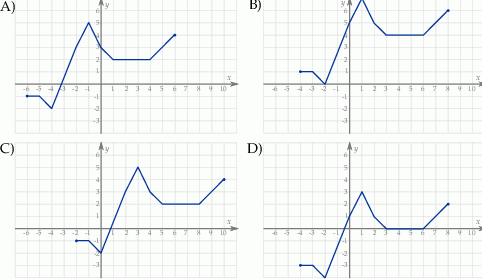
Wykres funkcji 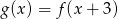 jest przedstawiony na rysunku:
jest przedstawiony na rysunku:
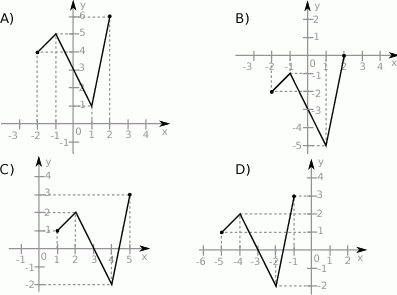
Poniżej przedstawiony jest wykres funkcji 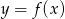 .
.
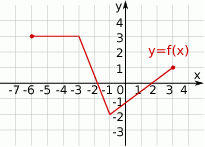
Wskaż wykres funkcji 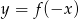 .
.
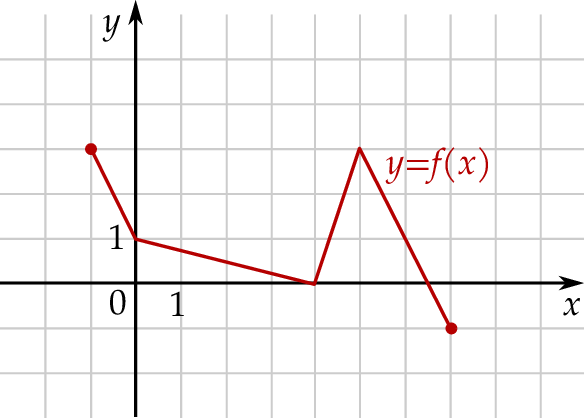
Rysunek przedstawia wykres funkcji 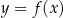 .
.
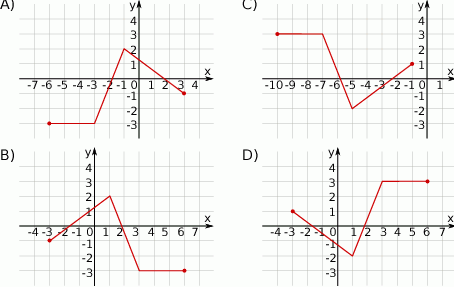
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 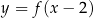 .
.
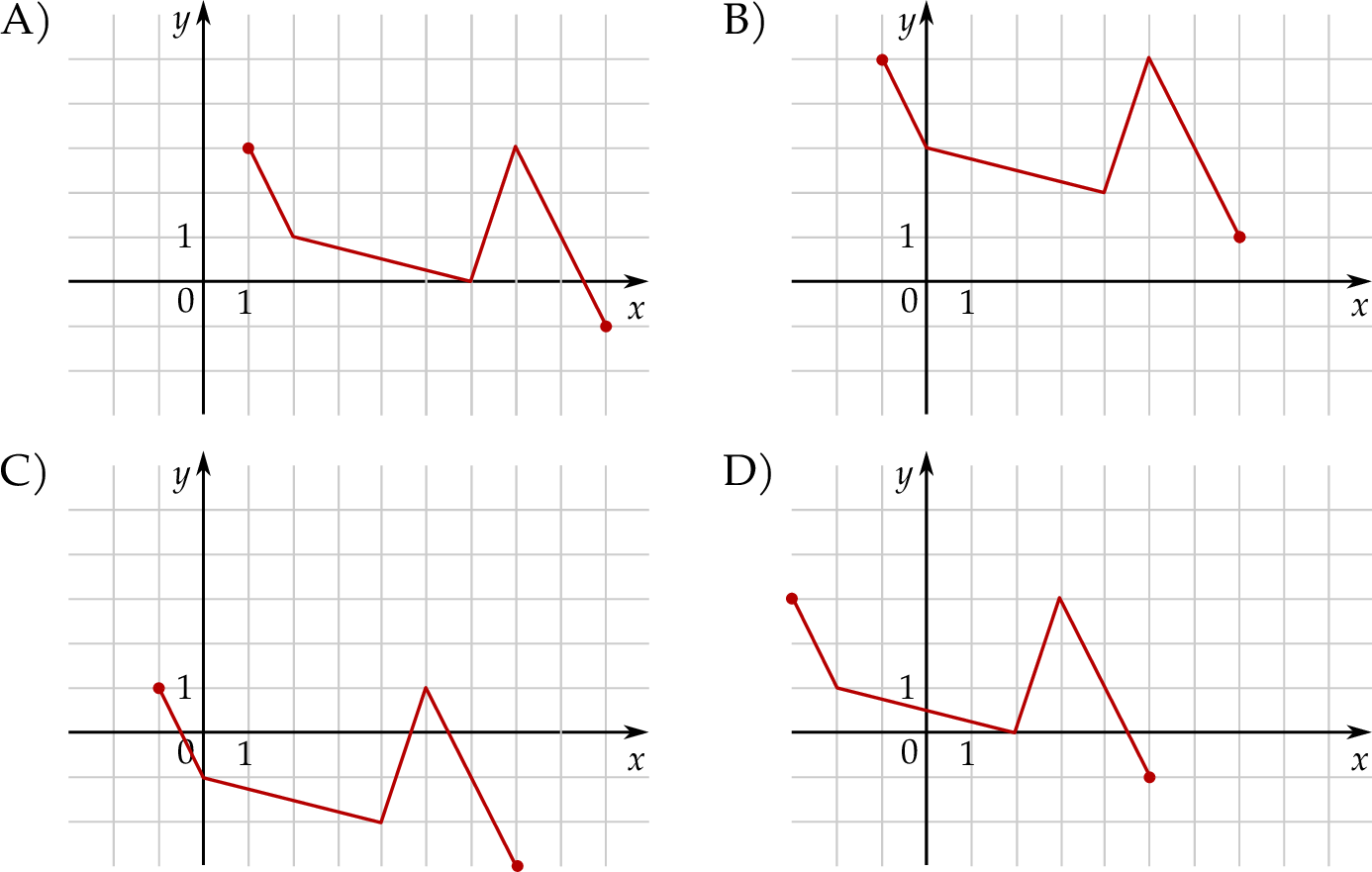
Rysunek przedstawia wykres funkcji 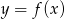 .
.
Wskaż wykres funkcji 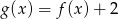 .
.
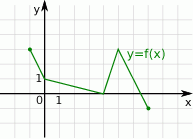
Rysunek przedstawia wykres funkcji 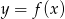 .
.
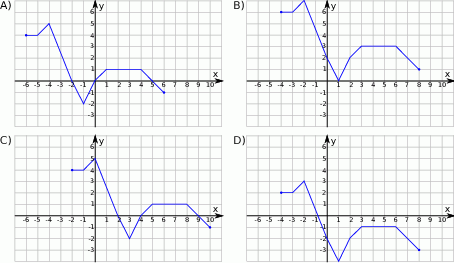
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 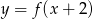 .
.
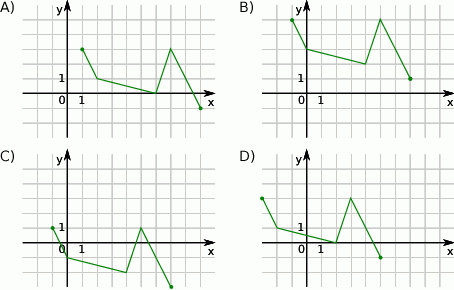
Rysunek przedstawia wykres funkcji 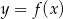 .
.
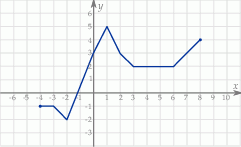
Wskaż wykres funkcji 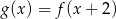 .
.
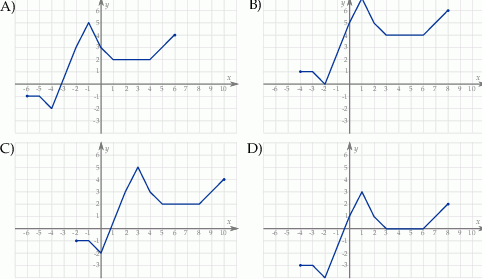
Rysunek przedstawia wykres funkcji 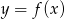 .
.
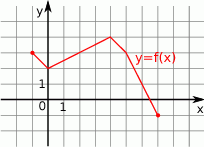
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 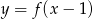 .
.
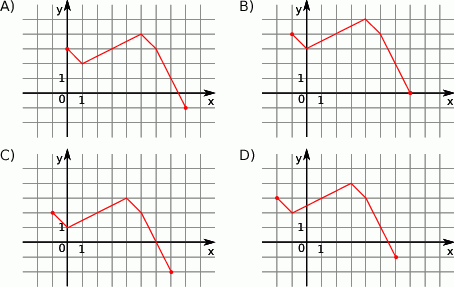
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
A) 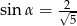 B)
B) 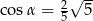 C)
C) 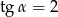 D)
D) 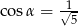
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Natomiast przeciwprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Natomiast przeciwprostokątna ma długość 6 cm. Zatem
A) 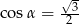 B)
B) 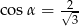 C)
C) 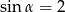 D)
D) 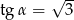
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
A) 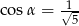 B)
B) 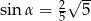 C)
C) 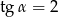 D)
D) 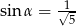
Oblicz dla jakich wartości parametrów 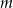 i
i  proste o równaniach:
proste o równaniach: 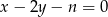 i
i 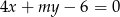 są dwiema różnymi prostymi równoległymi.
są dwiema różnymi prostymi równoległymi.
Wykaż, że równanie 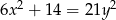 nie ma rozwiązań całkowitych.
nie ma rozwiązań całkowitych.
Posługując się wykresem funkcji 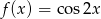 dla
dla 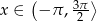 , rozwiąż nierówność
, rozwiąż nierówność 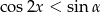 wiedząc, że miara kąta
wiedząc, że miara kąta  jest równa mierze łukowej kąta środkowego okręgu opartego na
jest równa mierze łukowej kąta środkowego okręgu opartego na 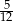 okręgu.
okręgu.
W malejącym ciągu geometrycznym 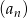 mamy
mamy 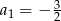 i
i 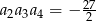 . Iloraz tego ciągu równy
. Iloraz tego ciągu równy
A) 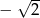 B)
B) 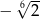 C)
C) 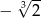 D)
D) 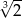
Dany jest ciąg 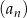 określony wzorem
określony wzorem 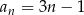 dla każdej liczby naturalnej
dla każdej liczby naturalnej 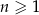 . Najmniejszą wartością
. Najmniejszą wartością  , dla której wyraz
, dla której wyraz 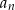 jest większy od 25, jest
jest większy od 25, jest
A) 8 B) 9 C) 7 D) 26
Dany jest ciąg 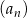 określony wzorem
określony wzorem 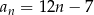 dla każdej liczby naturalnej
dla każdej liczby naturalnej 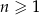 . Najmniejszą wartością
. Najmniejszą wartością  , dla której wyraz
, dla której wyraz 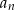 jest większy od 2023, jest
jest większy od 2023, jest
A) 170 B) 169 C) 168 D) 203
Przekątna 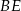 ściany bocznej prostopadłościanu
ściany bocznej prostopadłościanu 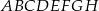 tworzy z krawędzią podstawy
tworzy z krawędzią podstawy 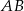 kąt o mierze
kąt o mierze 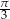 . Przekątne
. Przekątne 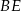 i
i 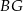 ścian bocznych tworzą kąt, którego cosinus jest równy
ścian bocznych tworzą kąt, którego cosinus jest równy 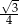 , a krawędź
, a krawędź 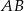 podstawy ma długość 2. Oblicz promień okręgu opisanego na trójkącie
podstawy ma długość 2. Oblicz promień okręgu opisanego na trójkącie 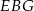 .
.
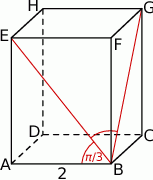
Dana jest funkcja 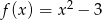 . Znajdź miejsca zerowe funkcji
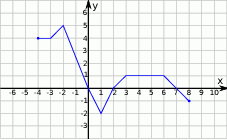
. Znajdź miejsca zerowe funkcji ![g(x ) = [f(x)]](https://img.zadania.info/zad/9606251/HzadT1x.gif) , gdzie
, gdzie ![[a]](https://img.zadania.info/zad/9606251/HzadT2x.gif) oznacza największą liczbę całkowitą nie większą od
oznacza największą liczbę całkowitą nie większą od  .
.
Rozwiąż równanie 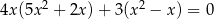 .
.
Odległość środka wysokości stożka od jego powierzchni bocznej jest trzy razy mniejsza niż promień jego podstawy. Oblicz sinus kąta rozwarcia stożka.
W trójkącie równoramiennym 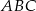 o podstawie
o podstawie 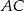 dane są:
dane są: 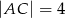 oraz
oraz 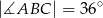 . Odcinek
. Odcinek 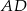 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta 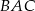 (zobacz rysunek).
(zobacz rysunek).
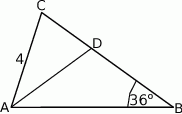
Oblicz długość odcinka 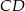 .
.
Wyznacz wszystkie wartości parametru 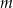 , dla których równanie
, dla których równanie
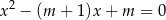
ma dwa różne rozwiązania rzeczywiste 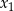 oraz
oraz 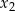 , spełniające warunki:
, spełniające warunki:
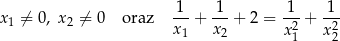
Kąt  jest kątem ostrym i
jest kątem ostrym i 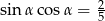 . Wówczas wyrażenie
. Wówczas wyrażenie 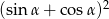 jest równe
jest równe
A)  B)
B)  C)
C) 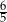 D) 1
D) 1
Kąt  jest kątem ostrym i
jest kątem ostrym i 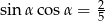 . Wówczas wyrażenie
. Wówczas wyrażenie 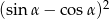 jest równe
jest równe
A) 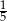 B)
B)  C)
C)  D) 1
D) 1
Kąt  jest kątem ostrym i
jest kątem ostrym i 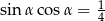 . Wówczas wyrażenie
. Wówczas wyrażenie 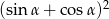 jest równe
jest równe
A)  B)
B) 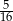 C)
C)  D) 1
D) 1
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 18 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 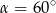 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 12 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 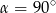 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 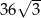 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
, a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 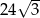 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
, a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.
Wyrażenie 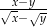 jest równe
jest równe
A) 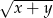 B)
B) 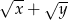 C)
C) 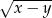 D)
D) 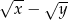
Wyrażenie 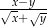 jest równe
jest równe
A) 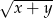 B)
B) 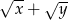 C)
C) 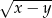 D)
D) 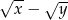
Suma trzech liczb tworzących ciąg geometryczny jest równa 26, a ich iloczyn jest równy 216. Wyznacz ten ciąg.
Trzy liczby dodatnie tworzą rosnący ciąg geometryczny o sumie równej 62. Suma logarytmów dziesiętnych tych liczb jest równa 3. Wyznacz te liczby.
Suma trzech liczb tworzących ciąg geometryczny jest równa 63, a ich iloczyn jest równy 5832. Wyznacz ten ciąg.
Wyznacz trzywyrazowy ciąg geometryczny, w którym suma trzech kolejnych wyrazów jest równa 84, a ich iloczyn jest równy 13824.
Uzasadnij, że dla dowolnej liczby naturalnej 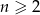 spełniona jest równość
spełniona jest równość