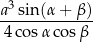Dany jest nieskończony ciąg geometryczny, w którym iloraz jest trzy razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa  . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A)  B)
B)  C)
C)  D) 7
D) 7
/Szkoła średnia
Dany jest nieskończony ciąg geometryczny, w którym iloraz jest trzy razy mniejszy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 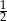 . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A) 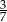 B)
B) 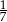 C)
C)  D) 7
D) 7
W urnie znajdują się jedynie kule białe i czarne. Kul białych jest trzy razy więcej niż czarnych. Oblicz, ile jest kul w urnie, jeśli przy jednoczesnym losowaniu dwóch kul prawdopodobieństwo otrzymania kul o różnych kolorach jest większe od 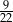 .
.
Dziedziną funkcji 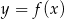 jest przedział
jest przedział 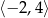 . Zatem dziedziną funkcji
. Zatem dziedziną funkcji 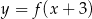 jest zbiór
jest zbiór
A) 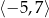 B)
B) 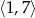 C)
C) 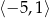 D)
D) 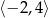
Dziedziną funkcji 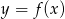 jest przedział
jest przedział 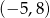 . Zatem dziedziną funkcji
. Zatem dziedziną funkcji 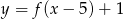 jest przedział
jest przedział
A) 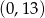 B)
B) 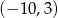 C)
C) 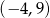 D)
D) 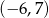
Dziedziną funkcji 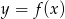 jest przedział
jest przedział 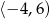 . Zatem dziedziną funkcji
. Zatem dziedziną funkcji 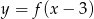 jest zbiór
jest zbiór
A) 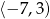 B)
B) 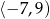 C)
C) 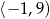 D)
D) 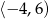
Funkcja 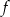 każdej liczbie naturalnej ze zbioru
każdej liczbie naturalnej ze zbioru 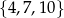 przyporządkowywuje resztę z dzielenia tej liczby przez 3. Zbiorem wartości tej funkcji jest zbiór
przyporządkowywuje resztę z dzielenia tej liczby przez 3. Zbiorem wartości tej funkcji jest zbiór
A) 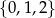 B)
B) 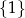 C)
C) 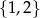 D)
D) 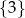
Funkcja 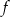 każdej liczbie naturalnej ze zbioru
każdej liczbie naturalnej ze zbioru 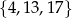 przyporządkowywuje resztę z dzielenia tej liczby przez 5. Zbiorem wartości tej funkcji jest zbiór
przyporządkowywuje resztę z dzielenia tej liczby przez 5. Zbiorem wartości tej funkcji jest zbiór
A) 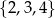 B)
B) 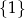 C)
C) 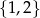 D)
D) 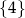
Funkcja 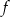 każdej liczbie naturalnej ze zbioru
każdej liczbie naturalnej ze zbioru 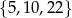 przyporządkowywuje resztę z dzielenia tej liczby przez 4. Zbiorem wartości tej funkcji jest zbiór
przyporządkowywuje resztę z dzielenia tej liczby przez 4. Zbiorem wartości tej funkcji jest zbiór
A) 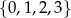 B)
B) 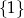 C)
C) 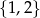 D)
D) 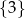
Dla jakich wartości parametru 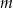 równanie
równanie 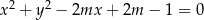 opisuje okrąg?
opisuje okrąg?
- Podaj współrzędne środka i długość promienia okręgu.
- Dla jakich wartości parametru
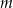 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 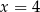 ?
?
Rozwiąż nierówność 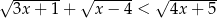 .
.
Wykaż, że istnieje liczba dodatnia  , dla której
, dla której 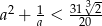 .
.
Rozwiąż równanie
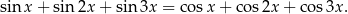
Na płaszczyźnie, w kartezjańskim układzie współrzędnych  , dane są punkty
, dane są punkty 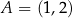 oraz
oraz 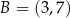 . Punkty
. Punkty 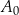 oraz
oraz 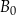 są odpowiednio obrazami punktów
są odpowiednio obrazami punktów 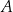 i
i 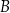 w symetrii środkowej o środku w punkcie
w symetrii środkowej o środku w punkcie 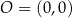 . Współczynnik kierunkowy prostej przechodzącej przez punkty
. Współczynnik kierunkowy prostej przechodzącej przez punkty 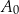 i
i 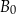 jest równy
jest równy
A)  B)
B) 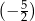 C)
C)  D)
D) 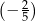
Rozwiąż równanie 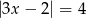 .
.
Rozwiąż równanie 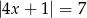 .
.
Rozwiąż równanie 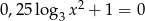 .
.
Rozwiąż równanie 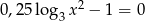 .
.
Podstawą ostrosłupa  jest kwadrat
jest kwadrat 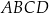 (patrz rysunek).
(patrz rysunek).
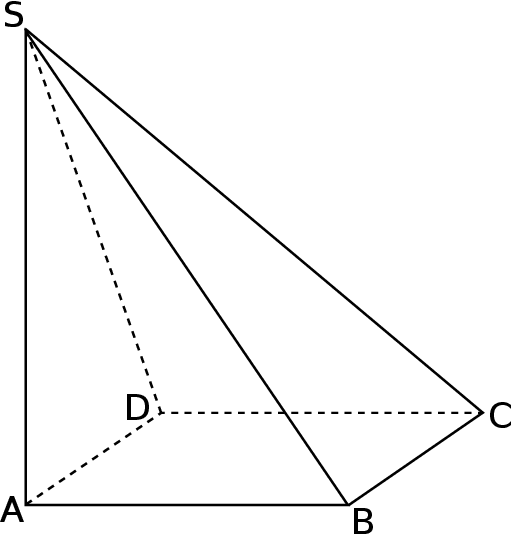
Krawędź 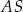 jest wysokością tego ostrosłupa. Odległość punktu
jest wysokością tego ostrosłupa. Odległość punktu 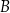 od krawędzi
od krawędzi 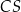 jest równa
jest równa 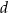 , a kąt dwuścienny między ścianami
, a kąt dwuścienny między ścianami 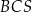 i
i 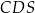 ma miarę
ma miarę 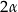 , gdzie
, gdzie 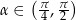 . Oblicz:
. Oblicz:
-
odległość punktu
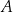 od krawędzi
od krawędzi 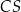
-
wysokość tego ostrosłupa.
W pewnym zakładzie pracy zależność przychodów ze sprzedaży od wielkości produkcji wyraża w przybliżeniu wzór 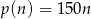 , gdzie
, gdzie  oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność
oznacza liczbę sztuk wyprodukowanego towaru, a koszty produkcji, w złotych, określa zależność 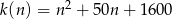 .
.
- Napisz wzór funkcji
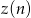 - zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji.
- zależności zysku zakładu od wielkości produkcji, jeśli wiadomo, że zysk jest różnicą między przychodem zakładu a kosztami produkcji. - Przy jakiej wielkości produkcji zysk wynosi 0?
- Jaka wielkość produkcji zapewnia największy zysk? Jaki jest koszt produkcji, gdy zysk jest największy?
Rodzinna firma stolarska produkuje małe wiatraki ogrodowe. Na podstawie analizy rzeczywistych wpływów i wydatków stwierdzono, że przychód  (w złotych) z tygodniowej sprzedaży
(w złotych) z tygodniowej sprzedaży  wiatraków można opisać funkcją
wiatraków można opisać funkcją
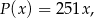
a koszt 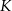 (w złotych) produkcji
(w złotych) produkcji  wiatraków w ciągu jednego tygodnia można określić funkcją
wiatraków w ciągu jednego tygodnia można określić funkcją
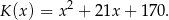
Tygodniowo w zakładzie można wyprodukować co najwyżej 150 wiatraków. Oblicz, ile tygodniowo wiatraków należy sprzedać, aby zysk zakładu w ciągu jednego tygodnia był największy. Oblicz ten największy zysk.
Zakład stolarski produkuje krzesła, które sprzedaje po 196 złotych za sztukę. Właściciel, na podstawie analizy rzeczywistych wpływów i wydatków, stwierdził, że:
-
przychód
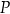 (w złotych) ze sprzedaży
(w złotych) ze sprzedaży  krzeseł można opisać funkcją
krzeseł można opisać funkcją 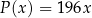
-
koszt
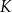 (w złotych) produkcji
(w złotych) produkcji  krzeseł dziennie można opisać funkcją
krzeseł dziennie można opisać funkcją 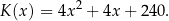
Dziennie w zakładzie można wyprodukować co najwyżej 30 krzeseł. Oblicz, ile krzeseł powinien dziennie sprzedawać zakład, aby zysk ze sprzedaży krzeseł wyprodukowanych przez ten zakład w ciągu jednego dnia był możliwie największy. Oblicz ten największy zysk.
Zakład stolarski produkuje stoły, które sprzedaje po 2144 złotych za sztukę. Właściciel, na podstawie analizy rzeczywistych wpływów i wydatków, stwierdził, że:
-
przychód
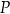 (w złotych) ze sprzedaży
(w złotych) ze sprzedaży  stołów można opisać funkcją
stołów można opisać funkcją 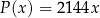
-
koszt
 (w złotych) produkcji
(w złotych) produkcji  stołów miesięcznie można opisać funkcją
stołów miesięcznie można opisać funkcją 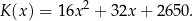
Miesięcznie w zakładzie można wyprodukować co najwyżej 80 stołów. Oblicz, ile stołów powinien miesięcznie sprzedawać zakład, aby zysk ze sprzedaży stołów wyprodukowanych przez ten zakład w ciągu jednego miesiąca był możliwie największy. Oblicz ten największy zysk.
Zakład ślusarski produkuje ozdobne kwietniki. Na podstawie analizy rzeczywistych wpływów i wydatków stwierdzono, że przychód  (w złotych) z tygodniowej sprzedaży
(w złotych) z tygodniowej sprzedaży  kwietników można opisać funkcją
kwietników można opisać funkcją
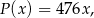
a koszt  (w złotych) produkcji
(w złotych) produkcji  kwietników w ciągu jednego tygodnia można określić funkcją
kwietników w ciągu jednego tygodnia można określić funkcją
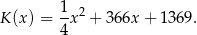
Tygodniowo w zakładzie można wyprodukować co najwyżej 250 kwietników. Oblicz, ile tygodniowo kwietników należy sprzedać, aby zysk zakładu w ciągu jednego tygodnia był największy. Oblicz ten największy zysk.
Wykaż, korzystając z twierdzenia o wymiernych pierwiastkach wielomianu, że liczba 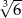 jest niewymierna.
jest niewymierna.
Wielomian 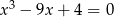 ma 3 pierwiastki rzeczywiste.
ma 3 pierwiastki rzeczywiste.
- Oblicz sumę odwrotności tych pierwiastków.
- Ustal, ile jest pierwiastków dodatnich.
- Oblicz odwrotność sumy kwadratów pierwiastków.
- Oblicz sumę kwadratów odwrotności tych pierwiastków.
Wykaż, że równanie 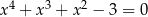 ma tylko jedno rozwiązanie które jest liczbą wymierną.
ma tylko jedno rozwiązanie które jest liczbą wymierną.
W ostrosłupie  podstawa
podstawa  jest trójkątem prostokątnym,
jest trójkątem prostokątnym, 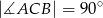 . Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość
. Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość  ostrosłupa ma długość 24 cm. Oblicz:
ostrosłupa ma długość 24 cm. Oblicz:
- objętość ostrosłupa;
- tangens kąta nachylenia ściany bocznej ostrosłupa, zawierającej przeciwprostokątną podstawy, do płaszczyzny podstawy.
Jeżeli 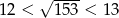 , to liczba
, to liczba 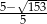 należy do przedziału:
należy do przedziału:
A) 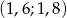 B)
B) 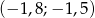 C)
C) 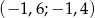 D)
D) 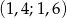
Jeżeli 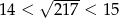 , to liczba
, to liczba 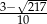 należy do przedziału:
należy do przedziału:
A) 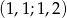 B)
B) 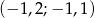 C)
C) 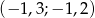 D)
D) 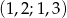
Jeżeli 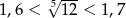 to liczba
to liczba 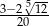 należy do przedziału
należy do przedziału
A) 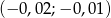 B)
B) 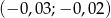 C)
C) 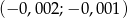 D)
D) 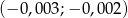
Oblicz sumę wszystkich rozwiązań równania
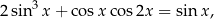
które należą do przedziału ![[− 8π ,24π]](https://img.zadania.info/zad/1020980/HzadT1x.png) .
.
Przez punkt 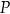 krawędzi bocznej
krawędzi bocznej 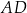 graniastosłupa prawidłowego trójkątnego
graniastosłupa prawidłowego trójkątnego 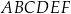 o krawędzi podstawy równej
o krawędzi podstawy równej  poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem
poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem  , a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem
, a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem 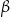 (zobacz rysunek).
(zobacz rysunek).
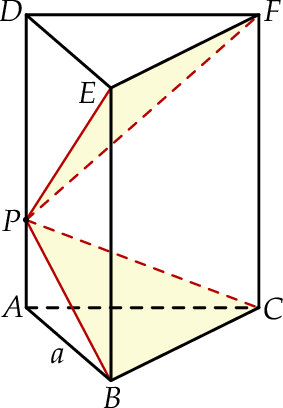
Udowodnij, że objętość ostrosłupa 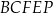 jest równa
jest równa