Oblicz granicę 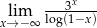 .
.
/Szkoła średnia
Oblicz granicę 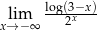 .
.
Suma dziewięciu początkowych wyrazów ciągu arytmetycznego wynosi 18, a suma siedmiu początkowych wyrazów jest równa 0. Wyrazy: siódmy, ósmy i dziewiąty są długościami boków trójkąta. Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu na nim opisanego.
Punkt 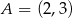 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 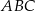 . Punkt
. Punkt 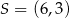 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 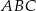 . Wskaż równanie okręgu wpisanego w trójkąt
. Wskaż równanie okręgu wpisanego w trójkąt 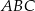 .
.
A) 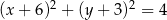 B)
B) 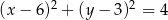
C) 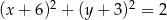 D)
D) 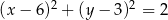
Punkt 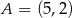 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 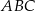 . Punkt
. Punkt 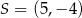 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 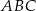 . Wskaż równanie okręgu wpisanego w trójkąt
. Wskaż równanie okręgu wpisanego w trójkąt 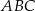 .
.
A) 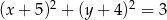 B)
B) 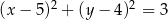
C) 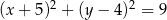 D)
D) 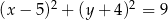
Miejscem zerowym funkcji 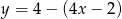 jest:
jest:
A) 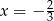 B)
B) 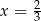 C)
C) 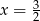 D)
D) 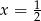
Miejscem zerowym funkcji liniowej 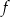 określonej wzorem
określonej wzorem 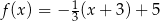 jest liczba
jest liczba
A) 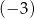 B)
B)  C) 5 D) 12
C) 5 D) 12
Miejscem zerowym funkcji 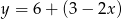 jest:
jest:
A) 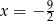 B)
B) 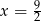 C)
C) 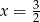 D)
D) 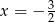
Funkcja liniowa określona jest wzorem 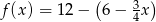 . Miejscem zerowym funkcji
. Miejscem zerowym funkcji 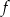 jest
jest
A) 8 B)  C)
C) 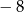 D)
D) 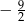
Cenę pewnego towaru obniżono najpierw o 30%, a potem o 50%. Początkowa cena została więc ostatecznie obniżona o 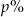 . Wynika stąd, że
. Wynika stąd, że
A) 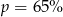 B)
B) 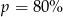 C)
C) 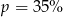 D)
D) 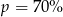
Cenę towaru obniżano dwa razy. Pierwsza obniżka wynosiła 10%, a druga 20%. O ile procent w wyniku obu obniżek spadła cena towaru?
A) o 24% B) o 26% C) o 28% D) o 30%
Cenę biurka obniżono o 10%, a następnie nową cenę obniżono o 30%. W wyniku obu tych zmian cena biurka zmniejszyła się w stosunku do ceny sprzed obu obniżek o
A) 43% B) 40% C) 37% D) 63%
Cenę książki obniżano dwukrotnie, najpierw o 10%, a po miesiącu jeszcze o 5%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 14% B) 14,5% C) 15% D) 15,5%
Cenę pewnego towaru podwyższono najpierw o 20%, a potem jeszcze o 10%. Rzeczywista podwyżka w procentach wyniosła
A) 20% B) 30% C) 32% D) 34%
Cena towaru została podwyższona o 30%, a po pewnym czasie nową, wyższą cenę ponownie podwyższono, tym razem o 10%. W rezultacie obu podwyżek wyjściowa cena towaru zwiększyła się o
A) 15% B) 20% C) 40% D) 43%
Cenę pewnego towaru obniżono najpierw o 20%, a potem o 30%. Początkowa cena została więc ostatecznie obniżona o 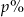 . Wynika stąd, że
. Wynika stąd, że
A) 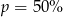 B)
B) 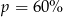 C)
C) 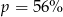 D)
D) 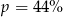
Cenę nart obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 30%. W wyniku obniżek cena nart zmniejszyła się o
A) 44% B) 50% C) 56% D) 60%
Cenę pewnego towaru obniżano dwukrotnie, za każdym razem o 20%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką
A) o 40% B) o 36% C) o 32% D) o 28%
Cenę drukarki obniżono o 20%, a następnie nową cenę obniżono o 10%. W wyniku obu tych zmian cena drukarki zmniejszyła się w stosunku do ceny sprzed obu obniżek o
A) 18% B) 28% C) 30% D) 72%
Cenę komputera obniżano dwukrotnie, najpierw o 20%, a po miesiącu jeszcze o 10%. W wyniku obu obniżek cena komputera zmniejszyła się o
A) 31% B) 30% C) 29% D) 28%
Cenę pewnego towaru obniżono o 20%, a następnie nową cenę tego towaru obniżono o 30%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką
A) o 50% B) o 56% C) o 44% D) o 66%
Cenę pewnego towaru podwyższono o 20%, a następnie nową cenę tego towaru podwyższono o 30%. Takie dwie podwyżki ceny tego towaru można zastąpić równoważną im jedną podwyżką
A) o 50% B) o 56% C) o 60% D) o 66%
Cenę książki obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 10%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 25% B) 28% C) 29% D) 30%
Cenę pewnego towaru obniżono najpierw o 40%, a potem o 70%. Początkowa cena została więc ostatecznie obniżona o 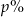 . Wynika stąd, że
. Wynika stąd, że
A) 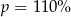 B)
B) 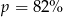 C)
C) 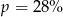 D)
D) 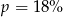
Cenę pewnego towaru podwyższono najpierw o 10%, a potem jeszcze o 10%. Rzeczywista podwyżka w procentach wyniosła
A) 20% B) 21% C) 22% D) 10%
Funkcja kwadratowa 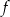 jest określona wzorem
jest określona wzorem 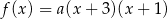 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 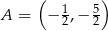 .
.
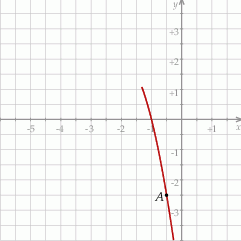
Współczynnik  we wzorze funkcji
we wzorze funkcji 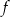 jest równy
jest równy
A) 1 B) 2 C) 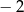 D)
D) 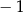
Funkcja kwadratowa 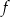 jest określona wzorem
jest określona wzorem 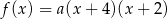 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 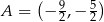 .
.
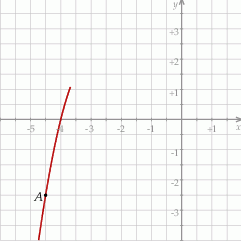
Współczynnik  we wzorze funkcji
we wzorze funkcji 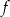 jest równy
jest równy
A) 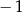 B)
B) 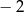 C) 2 D) 1
C) 2 D) 1
Granica 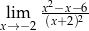
A) nie istnieje B) jest równa 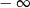 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 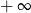
Granica 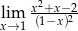
A) nie istnieje B) jest równa 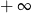 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 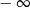
Granica 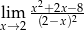
A) jest liczbą rzeczywistą B) nie istnieje C) jest równa 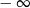 D) jest równa
D) jest równa 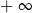
Granica 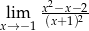
A) jest równa 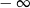 B) jest liczbą rzeczywistą C) nie istnieje D) jest równa
B) jest liczbą rzeczywistą C) nie istnieje D) jest równa 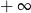
Granica 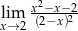
A) nie istnieje B) jest równa 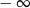 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 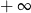
Granica 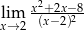
A) nie istnieje B) jest równa 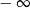 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 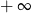
Granica 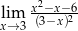
A) jest równa 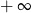 B) jest równa
B) jest równa 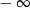 C) nie istnieje D) jest liczbą rzeczywistą
C) nie istnieje D) jest liczbą rzeczywistą
Granica 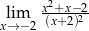
A) jest równa 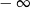 B) jest równa
B) jest równa 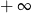 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego wynosi 6, a suma 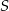 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 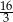 . Dla jakich naturalnych
. Dla jakich naturalnych  spełniona jest nierówność
spełniona jest nierówność 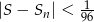 ?
?
Dla jakich wartości parametru  suma kwadratów różnych pierwiastków równania
suma kwadratów różnych pierwiastków równania
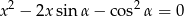
jest równa 3?
Dla jakiego 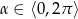 pierwiastki równania
pierwiastki równania
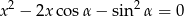
spełniają warunek 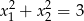 ?
?
Funkcja wykładnicza określona wzorem 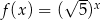 przyjmuje wartość 2 dla argumentu
przyjmuje wartość 2 dla argumentu
A) 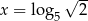 B)
B) 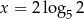 C)
C) 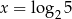 D)
D) 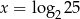
Funkcja wykładnicza określona wzorem 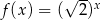 przyjmuje wartość 3 dla argumentu
przyjmuje wartość 3 dla argumentu
A) 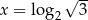 B)
B) 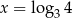 C)
C) 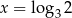 D)
D) 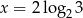
Objętość ostrosłupa prawidłowego czworokątnego jest równa 384. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 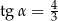 .
.
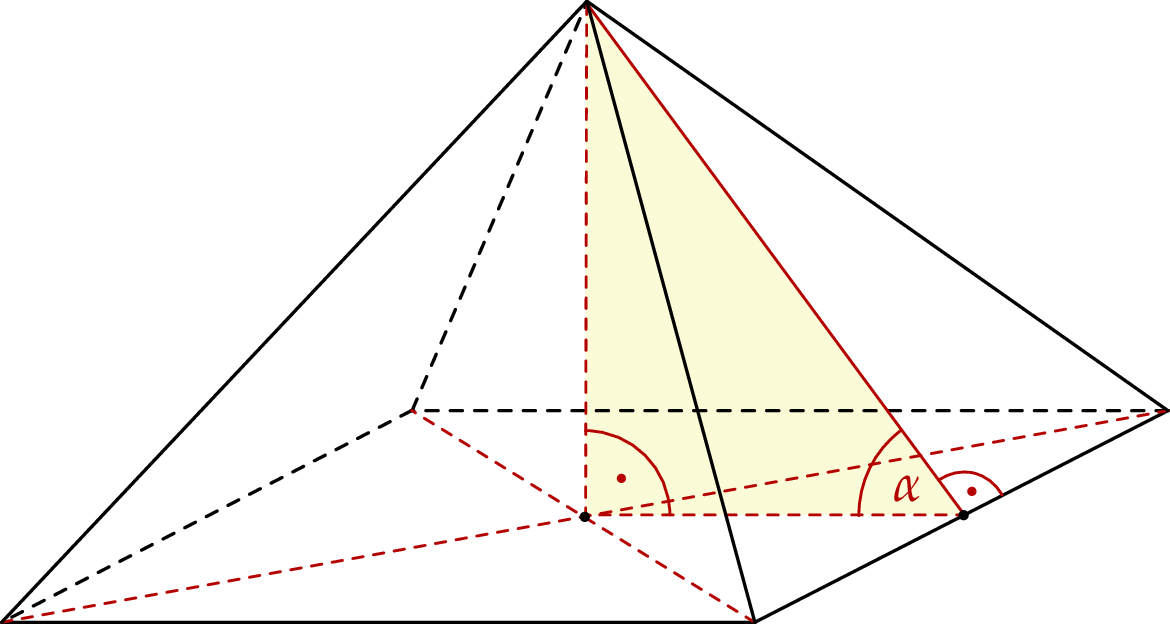
Oblicz wysokość ściany bocznej tego ostrosłupa.
Objętość ostrosłupa prawidłowego czworokątnego jest równa 400. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 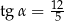 .
.
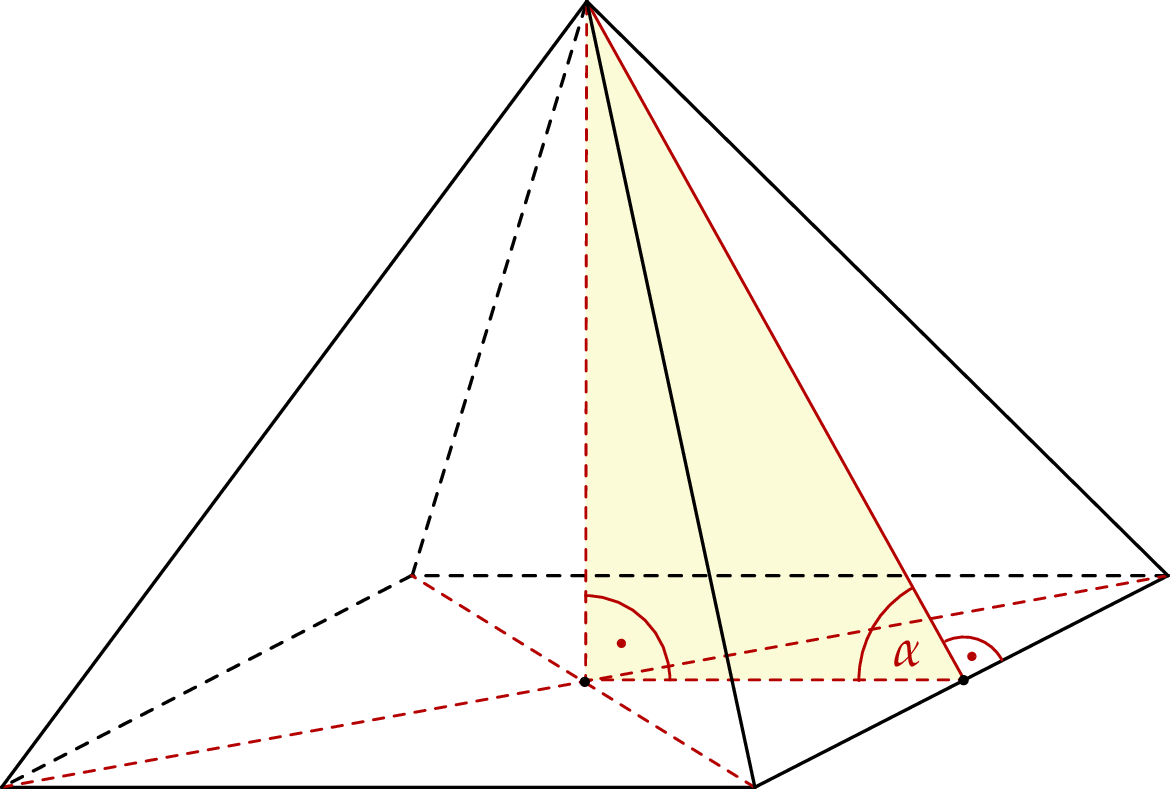
Oblicz wysokość ściany bocznej tego ostrosłupa.
Rozwiąż układ równań:
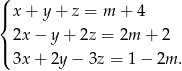
Dla jakich wartości parametru 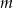 liczby
liczby 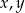 i
i  są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Obrazem trójkąta 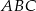 w podobieństwie o skali
w podobieństwie o skali 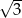 jest trójkąt
jest trójkąt 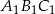 . Pole trójkąta
. Pole trójkąta 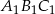 wynosi
wynosi 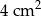 . Zatem pole trójkąta
. Zatem pole trójkąta 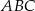 jest równe
jest równe
A) 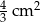 B)
B) 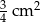 C)
C) 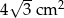 D)
D) 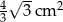
Pole trójkąta 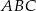 jest równe
jest równe 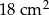 . Trójkąt
. Trójkąt 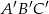 jest podobny do trójkąta
jest podobny do trójkąta 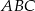 w skali
w skali 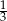 . Pole trójkąta
. Pole trójkąta 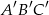 jest równe
jest równe
A) 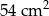 B)
B) 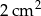 C)
C) 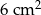 D)
D) 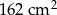
Pole trójkąta 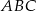 jest równe
jest równe 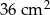 . Trójkąt
. Trójkąt 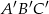 jest podobny do trójkąta
jest podobny do trójkąta 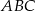 w skali
w skali 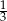 . Pole trójkąta
. Pole trójkąta 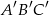 jest równe
jest równe
A) 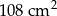 B)
B) 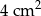 C)
C) 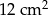 D)
D) 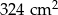
Trójkąt 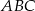 jest podobny do trójkąta
jest podobny do trójkąta 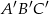 w skali
w skali  , przy czym
, przy czym 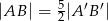 . Stosunek pola trójkąta
. Stosunek pola trójkąta 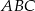 do pola trójkąta
do pola trójkąta 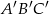 jest równy
jest równy
A) 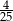 B)
B)  C)
C)  D)
D) 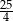
Obrazem trójkąta 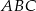 w podobieństwie o skali
w podobieństwie o skali 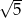 jest trójkąt
jest trójkąt 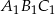 . Pole trójkąta
. Pole trójkąta 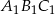 wynosi
wynosi 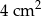 . Zatem pole trójkąta
. Zatem pole trójkąta 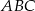 jest równe
jest równe
A) 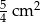 B)
B) 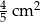 C)
C) 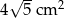 D)
D) 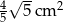
Obrazem trójkąta 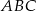 w podobieństwie o skali
w podobieństwie o skali 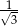 jest trójkąt
jest trójkąt 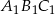 . Pole trójkąta
. Pole trójkąta 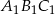 wynosi
wynosi 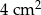 . Zatem pole trójkąta
. Zatem pole trójkąta 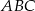 jest równe
jest równe
A) 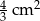 B)
B) 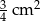 C)
C) 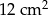 D)
D) 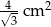
Na bokach 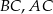 i
i 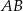 trójkąta
trójkąta 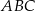 wybrano odpowiednio punkty
wybrano odpowiednio punkty 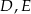 i
i 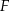 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 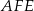 i
i 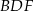 są styczne, to punkt
są styczne, to punkt 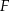 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 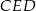 .
.
Ciąg geometryczny 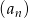 jest określony wzorem
jest określony wzorem 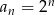 dla
dla 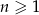 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 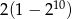 B)
B) 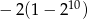 C)
C) 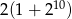 D)
D) 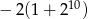
Ciąg geometryczny 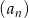 jest określony wzorem
jest określony wzorem 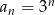 dla
dla 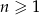 . Suma dziewięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziewięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 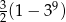 B)
B) 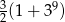 C)
C) 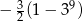 D)
D) 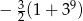
Wysokość 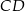 trójkąta równoramiennego
trójkąta równoramiennego 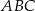 jest równa 8, a ramię
jest równa 8, a ramię 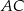 ma długość 10. Podstawa
ma długość 10. Podstawa 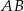 tego trójkąta ma długość
tego trójkąta ma długość
A) 12 B) 6 C) 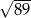 D)
D) 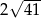
Wysokość 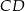 trójkąta równoramiennego
trójkąta równoramiennego 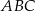 jest równa 10, a ramię
jest równa 10, a ramię 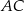 ma długość 14. Podstawa
ma długość 14. Podstawa 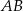 tego trójkąta ma długość
tego trójkąta ma długość
A) 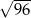 B)
B) 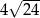 C)
C) 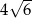 D)
D) 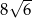
W trójkącie równoramiennym 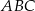 dane są
dane są 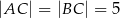 oraz wysokość
oraz wysokość 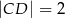 . Podstawa
. Podstawa 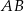 tego trójkąta ma długość
tego trójkąta ma długość
A) 6 B) 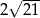 C)
C) 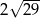 D) 14
D) 14
W trójkącie równoramiennym 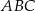 dane są
dane są 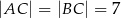 oraz wysokość
oraz wysokość 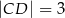 . Podstawa
. Podstawa 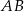 tego trójkąta ma długość
tego trójkąta ma długość
A) 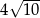 B)
B) 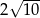 C)
C) 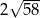 D) 10
D) 10
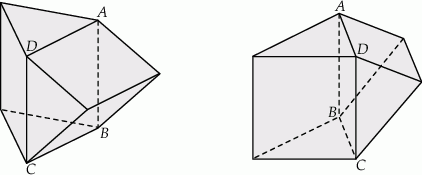
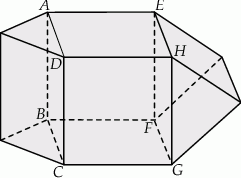
Na rysunkach przedstawiono tę samą bryłę widzianą z dwóch stron. Każda ze ścian tej bryły jest albo kwadratem, albo trójkątem równobocznym. Kwadratem jest też czworokąt 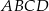 (patrz rysunki). Każda krawędź ma długość 2. Jaką objętość ma ta bryła? Zapisz obliczenia.
(patrz rysunki). Każda krawędź ma długość 2. Jaką objętość ma ta bryła? Zapisz obliczenia.
Na rysunku przedstawiono bryłę, której każda ściana jest albo kwadratem, albo trójkątem równobocznym. Kwadratami są też czworokąty 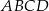 i
i  . Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.
. Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.
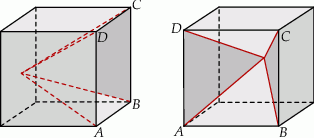
Z drewnianego sześcianu o krawędzi długości 6 cm wycięto ostrosłup prawidłowy czworokątny o wysokości równej krawędzi sześcianu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Jaką objętość ma ta bryła? Zapisz obliczenia.
Długości boków trójkąta prostokątnego, którego obwód jest równy 24cm tworzą ciąg arytmetyczny. Oblicz
- długość wysokości poprowadzonej z wierzchołka kąta prostego;
- wartość wyrażenia
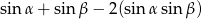 , gdzie
, gdzie  i
i 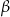 – miary kątów ostrych trójkąta.
– miary kątów ostrych trójkąta.
W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.
W graniastosłupie prawidłowym sześciokątnym krawędź boczna jest dwa razy dłuższa od krawędzi podstawy. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.
Rozwiąż równanie 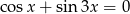 .
.
Rozwiąż równanie 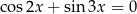 w zbiorze
w zbiorze ![[ π-π-] − 2, 2](https://img.zadania.info/zad/1617816/HzadT1x.png) .
.
Rozwiąż równanie 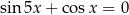 w zbiorze
w zbiorze ![[ π-π-] − 2,2](https://img.zadania.info/zad/3237491/HzadT1x.png) .
.

