Objętość ostrosłupa prawidłowego czworokątnego jest równa 384. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 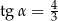 .
.
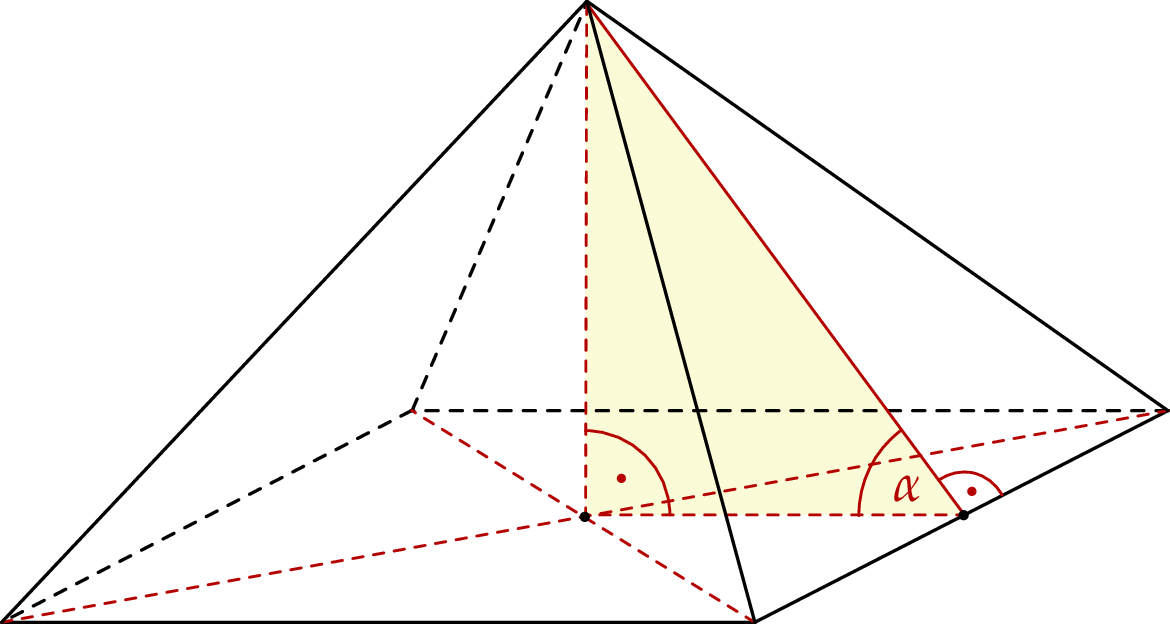
Oblicz wysokość ściany bocznej tego ostrosłupa.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Objętość ostrosłupa prawidłowego czworokątnego jest równa 384. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 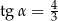 .
.

Oblicz wysokość ściany bocznej tego ostrosłupa.
Objętość ostrosłupa prawidłowego czworokątnego jest równa 400. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 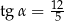 .
.
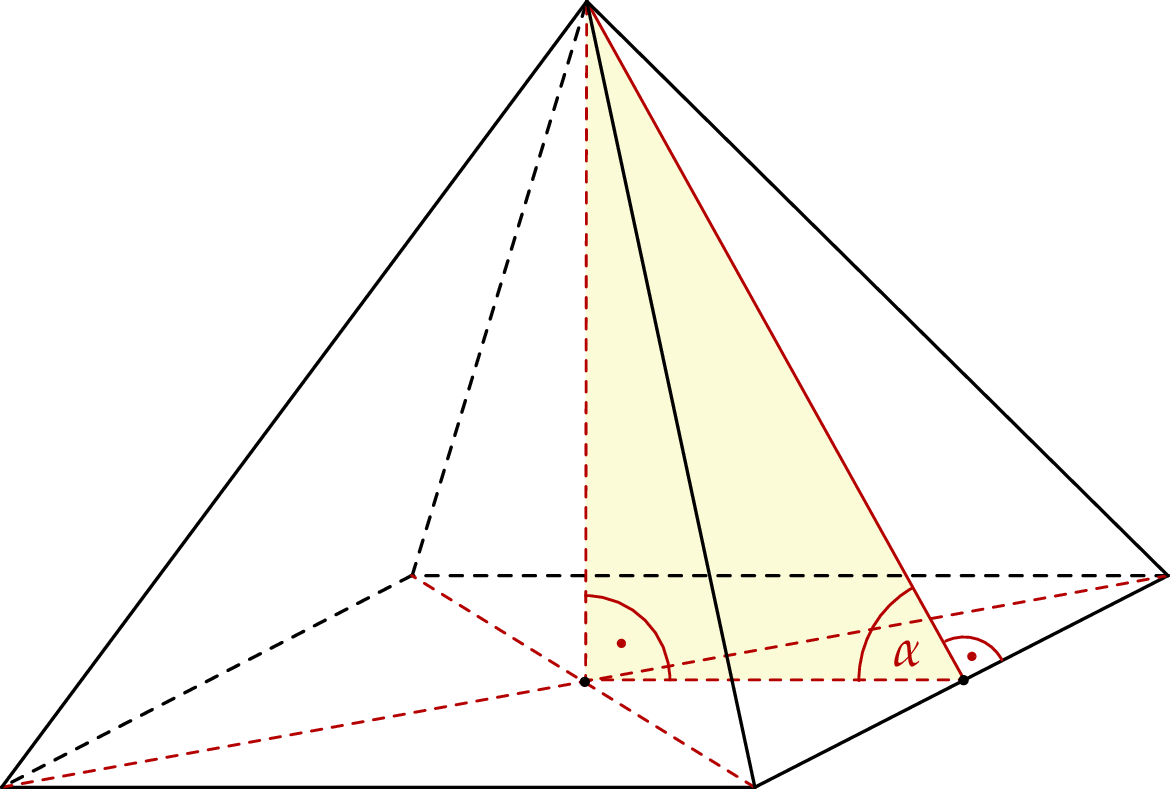
Oblicz wysokość ściany bocznej tego ostrosłupa.
Rozwiąż układ równań:
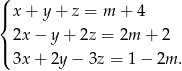
Dla jakich wartości parametru 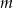 liczby
liczby 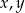 i
i  są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Obrazem trójkąta 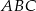 w podobieństwie o skali
w podobieństwie o skali 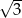 jest trójkąt
jest trójkąt 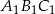 . Pole trójkąta
. Pole trójkąta 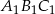 wynosi
wynosi 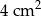 . Zatem pole trójkąta
. Zatem pole trójkąta 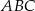 jest równe
jest równe
A) 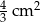 B)
B) 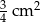 C)
C) 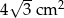 D)
D) 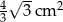
Pole trójkąta 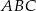 jest równe
jest równe 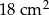 . Trójkąt
. Trójkąt 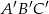 jest podobny do trójkąta
jest podobny do trójkąta 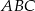 w skali
w skali 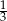 . Pole trójkąta
. Pole trójkąta 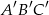 jest równe
jest równe
A) 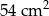 B)
B) 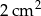 C)
C) 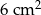 D)
D) 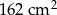
Pole trójkąta 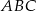 jest równe
jest równe 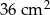 . Trójkąt
. Trójkąt 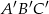 jest podobny do trójkąta
jest podobny do trójkąta 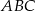 w skali
w skali 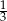 . Pole trójkąta
. Pole trójkąta 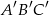 jest równe
jest równe
A) 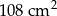 B)
B) 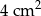 C)
C) 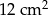 D)
D) 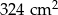
Trójkąt 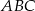 jest podobny do trójkąta
jest podobny do trójkąta 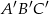 w skali
w skali  , przy czym
, przy czym 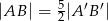 . Stosunek pola trójkąta
. Stosunek pola trójkąta 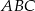 do pola trójkąta
do pola trójkąta 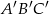 jest równy
jest równy
A) 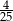 B)
B)  C)
C)  D)
D) 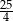
Obrazem trójkąta 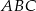 w podobieństwie o skali
w podobieństwie o skali 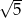 jest trójkąt
jest trójkąt 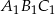 . Pole trójkąta
. Pole trójkąta 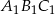 wynosi
wynosi 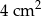 . Zatem pole trójkąta
. Zatem pole trójkąta 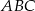 jest równe
jest równe
A) 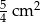 B)
B) 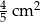 C)
C) 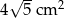 D)
D) 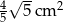
Obrazem trójkąta 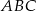 w podobieństwie o skali
w podobieństwie o skali 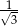 jest trójkąt
jest trójkąt 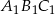 . Pole trójkąta
. Pole trójkąta 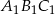 wynosi
wynosi 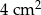 . Zatem pole trójkąta
. Zatem pole trójkąta 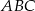 jest równe
jest równe
A) 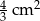 B)
B) 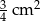 C)
C) 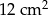 D)
D) 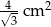
Na bokach 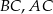 i
i 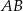 trójkąta
trójkąta 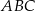 wybrano odpowiednio punkty
wybrano odpowiednio punkty 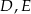 i
i 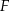 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 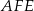 i
i 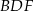 są styczne, to punkt
są styczne, to punkt 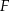 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 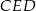 .
.
Ciąg geometryczny 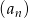 jest określony wzorem
jest określony wzorem 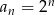 dla
dla 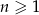 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 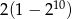 B)
B) 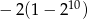 C)
C) 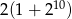 D)
D) 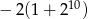
Ciąg geometryczny 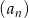 jest określony wzorem
jest określony wzorem 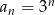 dla
dla 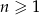 . Suma dziewięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziewięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 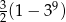 B)
B) 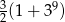 C)
C) 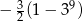 D)
D) 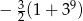
Wysokość 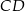 trójkąta równoramiennego
trójkąta równoramiennego 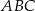 jest równa 8, a ramię
jest równa 8, a ramię 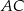 ma długość 10. Podstawa
ma długość 10. Podstawa 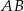 tego trójkąta ma długość
tego trójkąta ma długość
A) 12 B) 6 C) 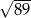 D)
D) 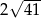
Wysokość 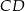 trójkąta równoramiennego
trójkąta równoramiennego 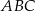 jest równa 10, a ramię
jest równa 10, a ramię 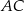 ma długość 14. Podstawa
ma długość 14. Podstawa 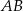 tego trójkąta ma długość
tego trójkąta ma długość
A) 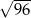 B)
B) 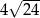 C)
C) 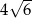 D)
D) 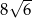
W trójkącie równoramiennym  dane są
dane są 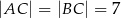 oraz wysokość
oraz wysokość 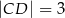 . Podstawa
. Podstawa 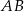 tego trójkąta ma długość
tego trójkąta ma długość
A) 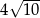 B)
B) 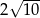 C)
C) 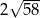 D) 10
D) 10
W trójkącie równoramiennym 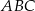 dane są
dane są 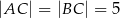 oraz wysokość
oraz wysokość 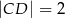 . Podstawa
. Podstawa 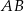 tego trójkąta ma długość
tego trójkąta ma długość
A) 6 B) 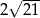 C)
C) 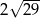 D) 14
D) 14
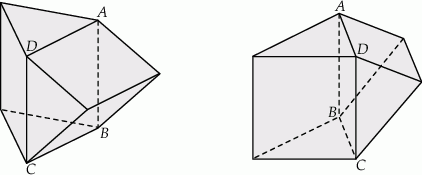
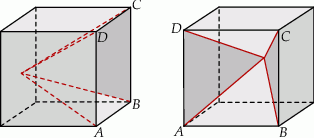
Na rysunkach przedstawiono tę samą bryłę widzianą z dwóch stron. Każda ze ścian tej bryły jest albo kwadratem, albo trójkątem równobocznym. Kwadratem jest też czworokąt 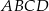 (patrz rysunki). Każda krawędź ma długość 2. Jaką objętość ma ta bryła? Zapisz obliczenia.
(patrz rysunki). Każda krawędź ma długość 2. Jaką objętość ma ta bryła? Zapisz obliczenia.
Na rysunku przedstawiono bryłę, której każda ściana jest albo kwadratem, albo trójkątem równobocznym. Kwadratami są też czworokąty  i
i 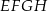 . Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.
. Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.
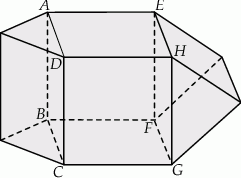
Z drewnianego sześcianu o krawędzi długości 6 cm wycięto ostrosłup prawidłowy czworokątny o wysokości równej krawędzi sześcianu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Jaką objętość ma ta bryła? Zapisz obliczenia.
Długości boków trójkąta prostokątnego, którego obwód jest równy 24cm tworzą ciąg arytmetyczny. Oblicz
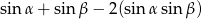 , gdzie
, gdzie  i
i 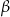 – miary kątów ostrych trójkąta.
– miary kątów ostrych trójkąta.W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.
W graniastosłupie prawidłowym sześciokątnym krawędź boczna jest dwa razy dłuższa od krawędzi podstawy. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.
Rozwiąż równanie 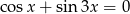 .
.
Rozwiąż równanie 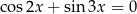 w zbiorze
w zbiorze ![[ π-π-] − 2, 2](https://img.zadania.info/zad/1617816/HzadT1x.png) .
.
Rozwiąż równanie 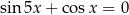 w zbiorze
w zbiorze ![[ π-π-] − 2,2](https://img.zadania.info/zad/3237491/HzadT1x.png) .
.
Ramiona kąta ostrego o mierze 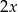 przecięto prostą
przecięto prostą 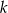 prostopadłą do dwusiecznej kąta, która jest odległa o
prostopadłą do dwusiecznej kąta, która jest odległa o 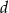 od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej
od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej 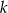 . Oblicz odległość środków tych okręgów.
. Oblicz odległość środków tych okręgów.
Punkt 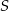 jest środkiem okręgu opisanego na trójkącie ostrokątnym
jest środkiem okręgu opisanego na trójkącie ostrokątnym 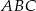 . Kąt
. Kąt 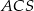 jest trzy razy większy od kąta
jest trzy razy większy od kąta 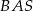 , a kąt
, a kąt 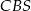 jest dwa razy większy od kąta
jest dwa razy większy od kąta 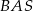 . Oblicz kąty trójkąta
. Oblicz kąty trójkąta 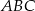 .
.
Punkt  jest środkiem okręgu opisanego na trójkącie rozwartokątnym
jest środkiem okręgu opisanego na trójkącie rozwartokątnym 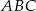 . Kąt
. Kąt 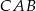 jest dwa razy większy od kąta
jest dwa razy większy od kąta 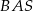 , a kąt
, a kąt 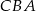 jest o
jest o 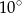 większy od kąta
większy od kąta 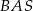 . Oblicz kąty trójkąta
. Oblicz kąty trójkąta 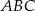 .
.
Do wykresu funkcji wykładniczej 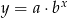 należą punkty
należą punkty 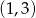 i
i 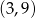 . Zatem liczba
. Zatem liczba 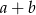 jest równa
jest równa
A) 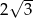 B) 12 C)
B) 12 C) 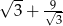 D)
D) 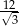
Do wykresu funkcji wykładniczej 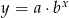 należą punkty
należą punkty 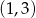 i
i 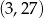 . Zatem liczba
. Zatem liczba 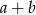 jest równa
jest równa
A) 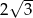 B) 12 C) 4 D)
B) 12 C) 4 D) 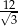
Podstawą ostrosłupa trójkątnego 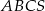 jest trójkąt prostokątny
jest trójkąt prostokątny 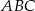 , w którym
, w którym 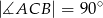 i
i 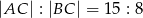 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 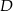 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 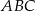 , a odcinek
, a odcinek 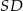 jest wysokością ostrosłupa. Objętość ostrosłupa jest równa 8, a pole ściany
jest wysokością ostrosłupa. Objętość ostrosłupa jest równa 8, a pole ściany 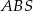 jest równe 17. Oblicz długość krawędzi
jest równe 17. Oblicz długość krawędzi 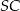 ostrosłupa
ostrosłupa
Po usunięciu jednej liczby z listy danych: 3, 2, 4, 1, 5, 1, 4, 1, 5, 2 średnia arytmetyczna zwiększyła się o 0,2. Którą liczbę usunięto z listy?
A) 1 B) 2 C) 3 D) 4
Po usunięciu jednej liczby z listy danych: 3, 2, 5, 4, 1, 5, 2, 4, 1, 5 średnia arytmetyczna zmniejszyła się o 0,2. Którą liczbę usunięto z listy?
A) 2 B) 3 C) 4 D) 5
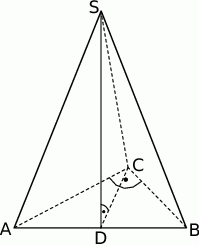
Dany jest ciąg arytmetyczny 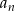 w którym
w którym 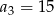 oraz
oraz 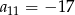 .
.
 zachodzi równość
zachodzi równość 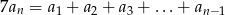 ?
? 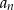 , które są podzielne przez 3.
, które są podzielne przez 3.W trójkącie równobocznym bok jest o 6 cm dłuższy od wysokości trójkąta. Oblicz pole i obwód tego trójkąta.
W trójkącie równobocznym wysokość jest o 3 cm krótsza od boku trójkąta. Oblicz pole i obwód tego trójkąta.
Miara kąta między ramionami trójkąta równoramiennego o polu 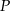 jest równa
jest równa  . Oblicz promień okręgu wpisanego w ten trójkąt.
. Oblicz promień okręgu wpisanego w ten trójkąt.
Przedstawiony na rysunku wykres może być wykresem funkcji
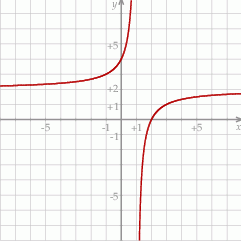
A) 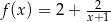 B)
B) 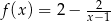 C)
C) 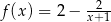 D)
D) 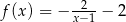
Przedstawiony na rysunku wykres może być wykresem funkcji
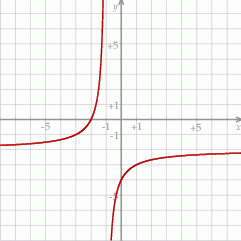
A) 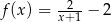 B)
B) 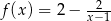 C)
C) 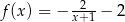 D)
D) 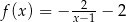
Dany jest graniastosłup prawidłowy trójkątny o podstawach 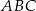 i
i 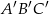 oraz krawędziach bocznych
oraz krawędziach bocznych 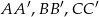 . Kąt nachylenia przekątnej ściany bocznej
. Kąt nachylenia przekątnej ściany bocznej 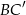 do płaszczyzny podstawy ma miarę
do płaszczyzny podstawy ma miarę  . Promień okręgu wpisanego w podstawę graniastosłupa ma długość
. Promień okręgu wpisanego w podstawę graniastosłupa ma długość  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
