Stosunek pól powierzchni dwóch kul jest równy 1:9. Wobec tego stosunek objętości tych kul jest równy
A) 1:3 B) 1:9 C) 1:27 D) 1:81
/Szkoła średnia
Stosunek pól powierzchni dwóch kul jest równy 1:4. Wobec tego stosunek objętości tych kul jest równy
A) 1:2 B) 1:8 C) 1:4 D) 1:16
Stosunek pól powierzchni dwóch kul jest równy 1:16. Wobec tego stosunek objętości tych kul jest równy
A) 1:256 B) 1:64 C) 1:16 D) 1:4
Podstawą ostrosłupa 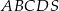 jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość
jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość 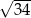 . Krawędź
. Krawędź 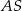 jest wysokością ostrosłupa oraz
jest wysokością ostrosłupa oraz 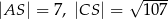 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Jeśli promień kuli zwiększymy o 30%, to pole powierzchni kuli wzrośnie o:
A) 30% B) 60% C) 69% D) ponad 100%
Jeśli promień kuli zmniejszymy o 50%, to pole powierzchni kuli zmaleje o:
A) 30% B) 60% C) 75% D) ponad 90%
Jeśli promień kuli zwiększymy o 50%, to pole powierzchni kuli wzrośnie o:
A) 30% B) 60% C) 69% D) ponad 100%
Automat biletowy drukuje 30 biletów w ciągu 2 minut i 6 sekund. Który wzór opisuje zależność między liczbą wydrukowanych biletów ( ), a czasem ich druku w sekundach (
), a czasem ich druku w sekundach (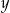 ), jeżeli tempo drukowania biletów nie ulega zmianie?
), jeżeli tempo drukowania biletów nie ulega zmianie?
A) 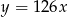 B)
B) 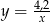 C)
C) 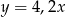 D)
D) 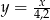
Jeżeli odcinek 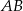 podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części (
podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części ( ), na którą dzielimy odcinek
), na którą dzielimy odcinek 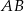 , a długością (
, a długością (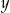 ) jednej takiej części w milimetrach?
) jednej takiej części w milimetrach?
A) 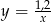 B)
B) 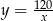 C)
C) 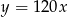 D)
D) 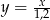
Ciąg 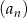 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 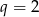 , w którym
, w którym 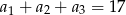 . Suma
. Suma 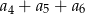 jest równa
jest równa
A) 136 B) 68 C) 34 D) 289
Ciąg 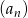 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 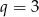 , w którym
, w którym 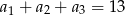 . Suma
. Suma 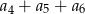 jest równa
jest równa
A) 39 B) 351 C) 117 D) 507
Dany jest stożek o polu powierzchni bocznej równym 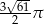 , w którym tangens kąta nachylenia tworzącej do podstawy jest równy
, w którym tangens kąta nachylenia tworzącej do podstawy jest równy  . Oblicz objętość tego stożka.
. Oblicz objętość tego stożka.
Odległość między środkami stycznych wewnętrznie okręgów o promieniach  i
i 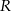 jest równa 7. Odległość między środkami stycznych zewnętrznie okręgów o promieniach
jest równa 7. Odległość między środkami stycznych zewnętrznie okręgów o promieniach  i
i 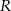 jest równa 23. Promienie
jest równa 23. Promienie  i
i 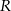 mają długości
mają długości
A) 6 i 17 B) 11 i 12 C) 10 i 13 D) 8 i 15
Wyrażenie 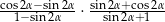 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 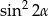 B)
B) 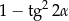 C)
C) 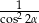 D)
D) 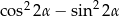
Wykaż, że dla dowolnych punktów płaszczyzny 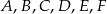 spełniona jest równość.
spełniona jest równość.
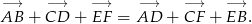
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 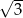 . Zatem
. Zatem
A) 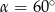 B)
B) 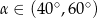 C)
C) 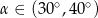 D)
D) 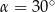
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 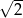 . Zatem
. Zatem
A) 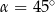 B)
B) 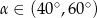 C)
C) 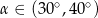 D)
D) 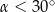
Wszystkie liczby trzycyfrowe uporządkowano malejąco. Mediana otrzymanego w ten sposób zestawu danych jest równa
A) 549,5 B) 550 C) 501 D) 599,5
Pole rombu o kącie ostrym 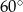 jest równe
jest równe 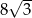 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 6 B) 2 C) 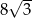 D) 4
D) 4
Pole rombu o kącie ostrym 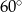 jest równe
jest równe 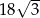 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 9 B) 3 C) 6 D) 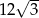
Dla jakich liczb naturalnych  , liczba
, liczba 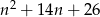 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Dla jakich liczb naturalnych  , liczba
, liczba 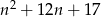 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Funkcje 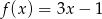 i
i 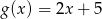 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 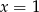 B)
B) 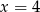 C)
C) 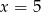 D)
D) 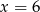
Funkcje 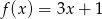 i
i 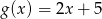 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 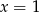 B)
B) 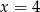 C)
C) 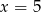 D)
D) 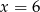
Funkcje 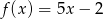 i
i 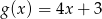 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 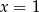 B)
B) 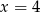 C)
C) 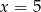 D)
D) 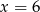
Funkcje 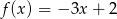 i
i 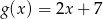 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 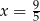 B)
B) 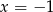 C)
C) 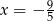 D)
D) 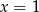
Długości boków trójkąta wychodzących z wierzchołka kąta ostrego  wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt
wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt  , jeśli pole tego trójkąta jest równe
, jeśli pole tego trójkąta jest równe 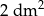 ?
?
A) 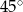 B)
B) 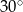 C)
C) 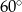 D)
D) 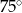
Długości wysokości trójkąta o bokach 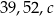 , gdzie
, gdzie 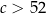 tworzą ciąg arytmetyczny. Oblicz promień okręgu wpisanego w ten trójkąt.
tworzą ciąg arytmetyczny. Oblicz promień okręgu wpisanego w ten trójkąt.
Okrąg 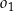 o środku w punkcie
o środku w punkcie 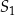 jest określony równaniem
jest określony równaniem 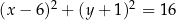 . Okrąg
. Okrąg 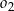 ma środek w punkcie
ma środek w punkcie 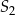 takim, że
takim, że ![−→ S 1S2 = [− 4,4]](https://img.zadania.info/zad/9553446/HzadT5x.png) . Promienie tych okręgów są sobie równe. Figura
. Promienie tych okręgów są sobie równe. Figura 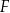 składa się z dwóch okręgów:
składa się z dwóch okręgów: 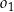 oraz
oraz 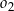 . Punkty
. Punkty 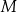 i
i 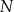 są punktami przecięcia figury
są punktami przecięcia figury 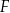 z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt
z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt 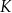 , leżący na jednej z osi symetrii figury
, leżący na jednej z osi symetrii figury 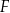 , taki, że pole trójkąta
, taki, że pole trójkąta 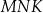 jest równe 40.
jest równe 40.
Dany jest trójkąt prostokątny o kącie ostrym 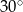 . Oblicz obwód tego trójkąta, jeżeli przeciwprostokątna ma długość 12 dm.
. Oblicz obwód tego trójkąta, jeżeli przeciwprostokątna ma długość 12 dm.
Z pudełka zawierającego dwa rodzaje monet wybieramy losowo dwie. Prawdopodobieństwo wybrania co najmniej jednej monety dwuzłotowej jest równe 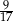 , a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe
, a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe 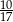 . Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
. Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
A) 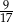 B)
B) 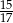 C)
C) 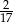 D)
D) 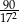
Na rysunku przedstawiony jest wykres funkcji 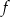 .
.
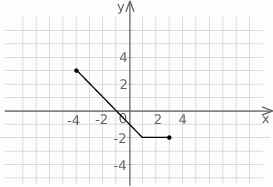
- Oblicz wartość wyrażenia
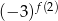 .
. - Podaj zbiór wartości funkcji
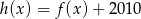 .
.

