Wszystkie liczby trzycyfrowe uporządkowano malejąco. Mediana otrzymanego w ten sposób zestawu danych jest równa
A) 549,5 B) 550 C) 501 D) 599,5
/Szkoła średnia
Pole rombu o kącie ostrym 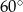 jest równe
jest równe 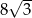 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 6 B) 2 C) 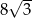 D) 4
D) 4
Pole rombu o kącie ostrym 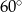 jest równe
jest równe 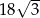 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 9 B) 3 C) 6 D) 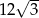
Dla jakich liczb naturalnych  , liczba
, liczba 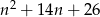 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Dla jakich liczb naturalnych  , liczba
, liczba 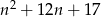 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Funkcje 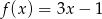 i
i 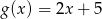 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 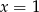 B)
B) 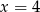 C)
C) 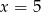 D)
D) 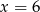
Funkcje 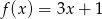 i
i 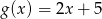 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 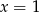 B)
B) 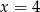 C)
C) 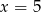 D)
D) 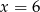
Funkcje 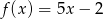 i
i 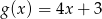 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 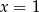 B)
B) 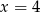 C)
C) 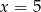 D)
D) 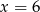
Funkcje 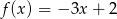 i
i 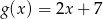 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 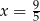 B)
B) 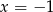 C)
C) 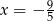 D)
D) 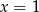
Długości boków trójkąta wychodzących z wierzchołka kąta ostrego  wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt
wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt  , jeśli pole tego trójkąta jest równe
, jeśli pole tego trójkąta jest równe 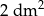 ?
?
A) 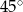 B)
B) 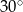 C)
C) 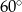 D)
D) 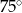
Długości wysokości trójkąta o bokach 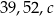 , gdzie
, gdzie 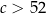 tworzą ciąg arytmetyczny. Oblicz promień okręgu wpisanego w ten trójkąt.
tworzą ciąg arytmetyczny. Oblicz promień okręgu wpisanego w ten trójkąt.
Okrąg 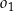 o środku w punkcie
o środku w punkcie 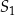 jest określony równaniem
jest określony równaniem 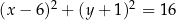 . Okrąg
. Okrąg 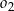 ma środek w punkcie
ma środek w punkcie 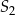 takim, że
takim, że ![−→ S 1S2 = [− 4,4]](https://img.zadania.info/zad/9553446/HzadT5x.png) . Promienie tych okręgów są sobie równe. Figura
. Promienie tych okręgów są sobie równe. Figura 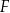 składa się z dwóch okręgów:
składa się z dwóch okręgów: 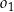 oraz
oraz 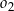 . Punkty
. Punkty 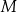 i
i 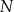 są punktami przecięcia figury
są punktami przecięcia figury 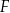 z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt
z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt 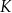 , leżący na jednej z osi symetrii figury
, leżący na jednej z osi symetrii figury 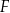 , taki, że pole trójkąta
, taki, że pole trójkąta 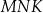 jest równe 40.
jest równe 40.
Dany jest trójkąt prostokątny o kącie ostrym 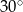 . Oblicz obwód tego trójkąta, jeżeli przeciwprostokątna ma długość 12 dm.
. Oblicz obwód tego trójkąta, jeżeli przeciwprostokątna ma długość 12 dm.
Z pudełka zawierającego dwa rodzaje monet wybieramy losowo dwie. Prawdopodobieństwo wybrania co najmniej jednej monety dwuzłotowej jest równe 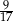 , a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe
, a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe 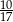 . Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
. Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
A) 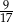 B)
B) 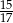 C)
C) 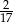 D)
D) 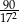
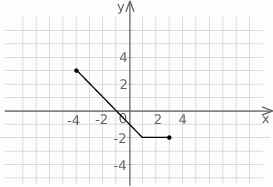
Na rysunku przedstawiony jest wykres funkcji 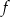 .
.
- Oblicz wartość wyrażenia
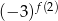 .
. - Podaj zbiór wartości funkcji
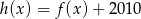 .
.
Rozwiąż równanie 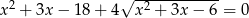 .
.
Dany jest prostopadłościan 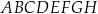 , w którym prostokąty
, w którym prostokąty 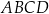 i
i 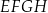 są jego podstawami. Odcinek
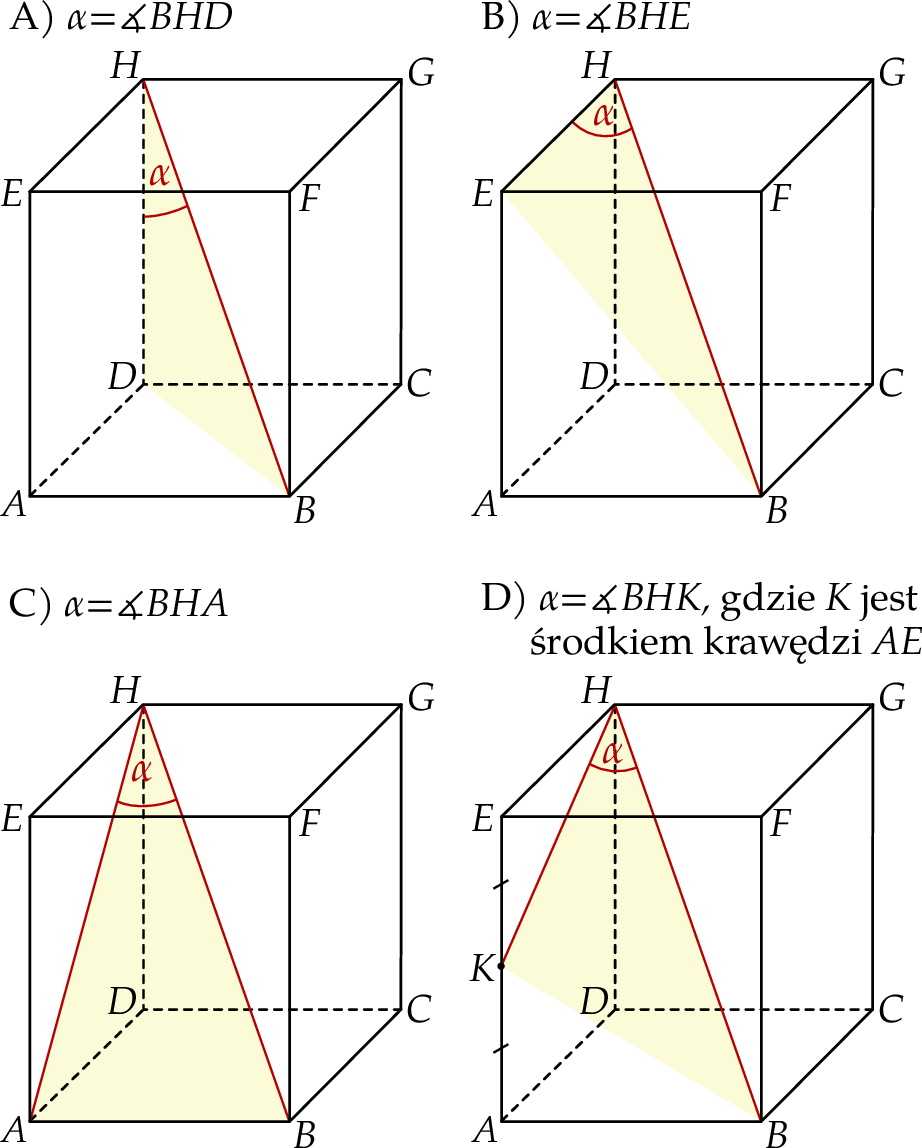
są jego podstawami. Odcinek 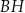 jest przekątną tego prostopadłościanu. Na którym rysunku prawidłowo oznaczono i podpisano kąt
jest przekątną tego prostopadłościanu. Na którym rysunku prawidłowo oznaczono i podpisano kąt  pomiędzy przekątną
pomiędzy przekątną 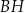 prostopadłościanu a jego ścianą boczną
prostopadłościanu a jego ścianą boczną 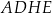 ?
?
Zaznacz w układzie współrzędnych zbiór punktów 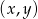 , dla których współrzędne spełniają nierówność
, dla których współrzędne spełniają nierówność 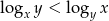 .
.
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod  takim, że
takim, że 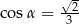 . Długość przekątnej tego graniastosłupa jest równa
. Długość przekątnej tego graniastosłupa jest równa
A) 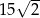 B) 45 C)
B) 45 C) 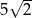 D) 10
D) 10
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 12. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod  takim, że
takim, że 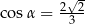 . Długość przekątnej tego graniastosłupa jest równa
. Długość przekątnej tego graniastosłupa jest równa
A) 18 B) 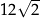 C)
C) 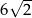 D) 8
D) 8
Na podstawie wykresu funkcji kwadratowej podaj jej wzór w postaci ogólnej, kanonicznej oraz iloczynowej.
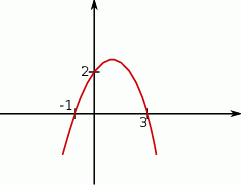
Oblicz, ile jest liczb naturalnych ośmiocyfrowych takich, że iloczyn cyfr w ich zapisie dziesiętnym jest równy 12.
Oblicz, ile jest liczb naturalnych ośmiocyfrowych takich, że iloczyn cyfr w ich zapisie dziesiętnym jest równy 8.
Oblicz, ile jest ośmiocyfrowych liczb naturalnych takich, że iloczyn wszystkich ich cyfr w zapisie dziesiętnym jest równy 1323.
Oblicz, ile jest liczb naturalnych czterocyfrowych takich, że iloczyn cyfr w ich zapisie dziesiętnym jest równy 36.
Oblicz, ile jest siedmiocyfrowych liczb naturalnych takich, że iloczyn wszystkich ich cyfr w zapisie dziesiętnym jest równy 28.
W trójkącie 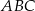 dane są długości boków:
dane są długości boków: 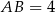 ,
, 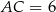 ,
, 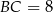 . Oblicz długości odcinków, na jakie dzieli bok
. Oblicz długości odcinków, na jakie dzieli bok 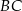 wysokość opuszczona z wierzchołka
wysokość opuszczona z wierzchołka 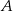 .
.
W wyniku zwiększenia każdego boku danego prostokąta o 2 cm jego pole wzrosło o 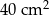 . O ile zwiększy się pole danego prostokąta, jeśli jego boki zwiększymy o 3 cm?
. O ile zwiększy się pole danego prostokąta, jeśli jego boki zwiększymy o 3 cm?
W wyniku zwiększenia każdego boku danego prostokąta o 2 cm jego pole wzrosło o 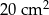 . O ile zwiększy się pole danego prostokąta, jeśli jego boki zwiększymy o 3 cm?
. O ile zwiększy się pole danego prostokąta, jeśli jego boki zwiększymy o 3 cm?
Ze zbioru 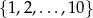 losujemy dwie różne liczby
losujemy dwie różne liczby  i
i 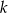 . Oblicz prawdopodobieństwo, że
. Oblicz prawdopodobieństwo, że
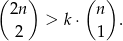
Puszka konserwy ma kształt walca. Jaką wysokość i jaki promień podstawy powinna mieć ta puszka, aby przy objętości puszki 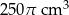 zużyć jak najmniej materiału na jej wykonanie.
zużyć jak najmniej materiału na jej wykonanie.

