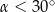Określ wzajemne położenie prostej 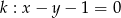 i okręgu o równaniu
i okręgu o równaniu 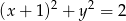 .
.
/Szkoła średnia
Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 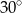 i
i 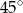 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
Dany jest trapez, w którym podstawy mają długość 6 cm i 20 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 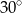 i
i 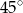 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
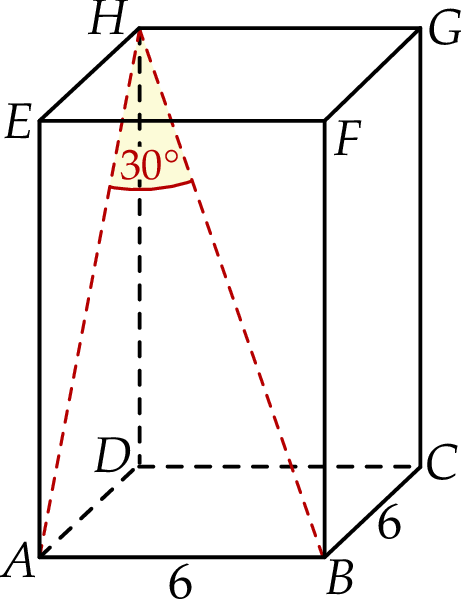
Dany jest prostopadłościan 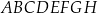 , w którym podstawy
, w którym podstawy 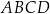 i
i 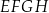 są kwadratami o boku długości 6. Przekątna
są kwadratami o boku długości 6. Przekątna 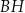 tego prostopadłościanu tworzy z przekątną
tego prostopadłościanu tworzy z przekątną 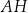 ściany bocznej
ściany bocznej 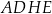 kąt o mierze
kąt o mierze 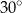 (zobacz rysunek).
(zobacz rysunek).
Przekątna 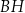 tego prostopadłościanu ma długość równą
tego prostopadłościanu ma długość równą
A) 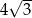 B)
B) 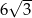 C) 12 D)
C) 12 D) 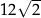
Pierwszy wyraz ciągu arytmetycznego jest równy 5, a suma jego pięciu początkowych wyrazów wynosi 55. Czwarty wyraz tego ciągu jest równy
A) 12 B) 13 C) 14 D) 15
Pierwszy wyraz ciągu arytmetycznego wynosi 7, suma siedmiu początkowych wyrazów ciągu jest równa 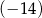 . Czwarty wyraz ciągu jest równy
. Czwarty wyraz ciągu jest równy
A) 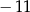 B)
B) 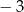 C)
C) 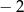 D) 16
D) 16
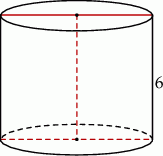
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
A) 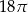 B)
B) 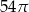 C)
C) 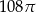 D)
D) 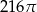
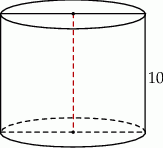
Przekrój osiowy walca jest kwadratem o boku 10. Objętość tego walca jest równa
A) 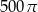 B)
B) 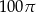 C)
C) 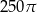 D)
D) 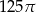
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
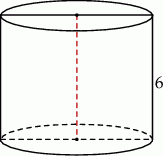
A) 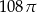 B)
B) 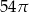 C)
C) 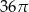 D)
D) 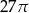
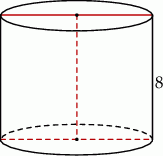
Przekrój osiowy walca jest kwadratem o boku długości 8. Objętość tego walca jest równa
A) 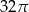 B)
B) 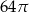 C)
C) 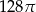 D)
D) 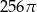
Jeżeli przekrój osiowy walca jest kwadratem o boku 4, to objętość walca jest równa
A) 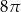 B)
B) 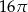 C)
C) 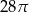 D)
D) 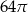
Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 15, jeśli wiadomo, że jest ona podzielna przez 18.
Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 18, jeśli wiadomo, że jest ona podzielna przez 24.
Punkt 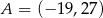 i środek
i środek 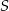 odcinka
odcinka 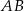 są położone symetrycznie względem początku układu współrzędnych. Zatem punkt
są położone symetrycznie względem początku układu współrzędnych. Zatem punkt 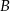 ma współrzędne
ma współrzędne
A) 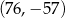 B)
B) 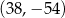 C)
C) 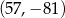 D)
D) 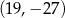
Punkt 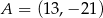 i środek
i środek 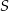 odcinka
odcinka 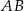 są położone symetrycznie względem początku układu współrzędnych. Zatem punkt
są położone symetrycznie względem początku układu współrzędnych. Zatem punkt 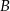 ma współrzędne
ma współrzędne
A) 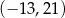 B)
B) 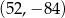 C)
C) 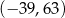 D)
D) 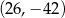
Długości boków 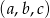 trójkąta tworzą ciąg geometryczny, przy czym kąt trójkąta leżący naprzeciwko boku długości
trójkąta tworzą ciąg geometryczny, przy czym kąt trójkąta leżący naprzeciwko boku długości 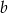 ma miarę
ma miarę 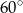 . Oblicz miary pozostałych kątów tego trójkąta.
. Oblicz miary pozostałych kątów tego trójkąta.
Dane są punkty 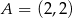 ,
, 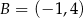 ,
, 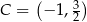 i
i 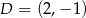 . Pole czworokąta
. Pole czworokąta 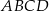 jest równe
jest równe
A) 10,5 B) 16,5 C) 9 D) 8,25
Trzy wychodzące z jednego wierzchołka krawędzie równoległościanu są równe 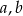 i
i  . Krawędzie
. Krawędzie  i
i 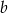 są prostopadłe, a krawędź
są prostopadłe, a krawędź  tworzy z każdą z nich kąt ostry
tworzy z każdą z nich kąt ostry  . Oblicz objętość równoległościanu.
. Oblicz objętość równoległościanu.
Stosunek pól powierzchni dwóch kul jest równy 1:9. Wobec tego stosunek objętości tych kul jest równy
A) 1:3 B) 1:9 C) 1:27 D) 1:81
Stosunek pól powierzchni dwóch kul jest równy 1:16. Wobec tego stosunek objętości tych kul jest równy
A) 1:256 B) 1:64 C) 1:16 D) 1:4
Stosunek pól powierzchni dwóch kul jest równy 1:4. Wobec tego stosunek objętości tych kul jest równy
A) 1:2 B) 1:8 C) 1:4 D) 1:16
Podstawą ostrosłupa 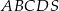 jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość
jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość 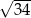 . Krawędź
. Krawędź 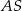 jest wysokością ostrosłupa oraz
jest wysokością ostrosłupa oraz 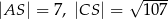 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Jeśli promień kuli zwiększymy o 30%, to pole powierzchni kuli wzrośnie o:
A) 30% B) 60% C) 69% D) ponad 100%
Jeśli promień kuli zmniejszymy o 50%, to pole powierzchni kuli zmaleje o:
A) 30% B) 60% C) 75% D) ponad 90%
Jeśli promień kuli zwiększymy o 50%, to pole powierzchni kuli wzrośnie o:
A) 30% B) 60% C) 69% D) ponad 100%
Automat biletowy drukuje 30 biletów w ciągu 2 minut i 6 sekund. Który wzór opisuje zależność między liczbą wydrukowanych biletów ( ), a czasem ich druku w sekundach (
), a czasem ich druku w sekundach (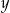 ), jeżeli tempo drukowania biletów nie ulega zmianie?
), jeżeli tempo drukowania biletów nie ulega zmianie?
A) 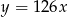 B)
B) 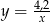 C)
C) 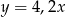 D)
D) 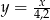
Jeżeli odcinek 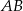 podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części (
podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części ( ), na którą dzielimy odcinek
), na którą dzielimy odcinek 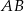 , a długością (
, a długością (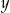 ) jednej takiej części w milimetrach?
) jednej takiej części w milimetrach?
A) 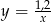 B)
B) 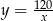 C)
C) 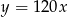 D)
D) 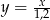
Ciąg 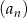 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 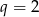 , w którym
, w którym 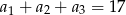 . Suma
. Suma 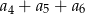 jest równa
jest równa
A) 136 B) 68 C) 34 D) 289
Ciąg 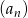 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 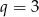 , w którym
, w którym 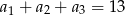 . Suma
. Suma 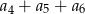 jest równa
jest równa
A) 39 B) 351 C) 117 D) 507
Dany jest stożek o polu powierzchni bocznej równym 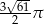 , w którym tangens kąta nachylenia tworzącej do podstawy jest równy
, w którym tangens kąta nachylenia tworzącej do podstawy jest równy  . Oblicz objętość tego stożka.
. Oblicz objętość tego stożka.
Odległość między środkami stycznych wewnętrznie okręgów o promieniach  i
i 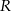 jest równa 7. Odległość między środkami stycznych zewnętrznie okręgów o promieniach
jest równa 7. Odległość między środkami stycznych zewnętrznie okręgów o promieniach  i
i 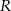 jest równa 23. Promienie
jest równa 23. Promienie  i
i 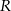 mają długości
mają długości
A) 6 i 17 B) 11 i 12 C) 10 i 13 D) 8 i 15
Wyrażenie 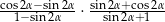 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 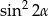 B)
B) 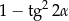 C)
C) 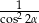 D)
D) 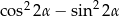
Wykaż, że dla dowolnych punktów płaszczyzny 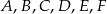 spełniona jest równość.
spełniona jest równość.
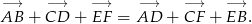
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 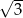 . Zatem
. Zatem
A) 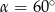 B)
B) 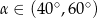 C)
C) 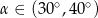 D)
D) 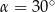
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 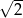 . Zatem
. Zatem
A) 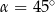 B)
B) 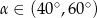 C)
C) 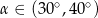 D)
D)