W kartezjańskim układzie współrzędnych 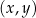 dana jest prosta
dana jest prosta 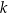 o równaniu
o równaniu 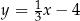 . Prosta o równaniu
. Prosta o równaniu 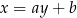 jest równoległa do prostej
jest równoległa do prostej 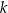 i przechodzi przez punkt
i przechodzi przez punkt 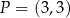 , gdy
, gdy
A) 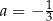 i
i 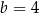 B)
B) 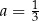 i
i 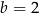 C)
C) 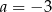 i
i 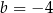 D)
D) 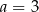 i
i 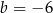
/Szkoła średnia
Proste 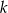 i
i 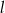 są równoległe do osi
są równoległe do osi 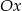 i przecinają wykres funkcji
i przecinają wykres funkcji 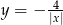 odpowiednio w punktach
odpowiednio w punktach 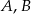 i
i 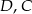 w ten sposób, że czworokąt
w ten sposób, że czworokąt 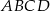 jest trapezem o polu 6 i wysokości 2. Oblicz obwód trapezu
jest trapezem o polu 6 i wysokości 2. Oblicz obwód trapezu 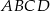 .
.
Miejsce zerowe funkcji liniowej 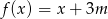 jest większe od 2 dla każdej liczby
jest większe od 2 dla każdej liczby 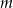 spełniającej warunek
spełniającej warunek
A) 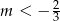 B)
B) 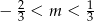 C)
C) 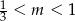 D)
D) 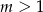
Podstawą ostrosłupa 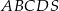 jest prostokąt o obwodzie 6. Krawędź
jest prostokąt o obwodzie 6. Krawędź 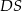 jest wysokością ostrosłupa i jest 3 razy dłuższa od krawędzi
jest wysokością ostrosłupa i jest 3 razy dłuższa od krawędzi 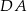 . Jakie największe pole może mieć przekrój ostrosłupa płaszczyzną wyznaczoną przez wierzchołki
. Jakie największe pole może mieć przekrój ostrosłupa płaszczyzną wyznaczoną przez wierzchołki 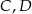 i środek krawędzi
i środek krawędzi 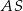 ?
?
Wykaż, że
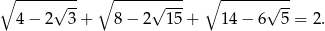
Dla każdej dodatniej liczby  wyrażenie
wyrażenie 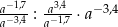 jest równe
jest równe
A) 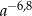 B)
B) 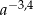 C) 1 D)
C) 1 D) 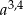
Wyrażenie 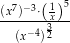 jest równe
jest równe
A) 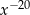 B)
B) 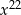 C)
C) 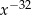 D)
D) 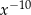
Wyznacz wszystkie rozwiązania równania 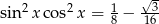 należące do przedziału
należące do przedziału 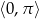 .
.
Wyznacz wszystkie rozwiązania równania 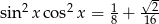 należące do przedziału
należące do przedziału 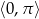 .
.
Suma trzech początkowych wyrazów ciągu geometrycznego wynosi 26, różnica wyrazów czwartego i pierwszego wynosi 52. Oblicz piąty wyraz tego ciągu.
Suma trzech początkowych wyrazów ciągu geometrycznego wynosi 21, różnica wyrazów czwartego i pierwszego wynosi 63. Oblicz piąty wyraz tego ciągu.
Dla jakich wartości parametru 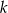 równanie
równanie 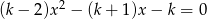 ma tylko ujemne rozwiązania?
ma tylko ujemne rozwiązania?
Dla jakich wartości 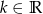 równanie
równanie 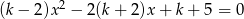 ma dwa różne pierwiastki dodatnie?
ma dwa różne pierwiastki dodatnie?
Wyznacz wszystkie wartości parametru 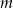 , dla których równanie
, dla których równanie 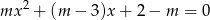 ma dwa rozwiązania dodatnie.
ma dwa rozwiązania dodatnie.
Dla jakich wartości 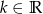 równanie
równanie 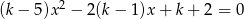 ma dwa różne pierwiastki dodatnie?
ma dwa różne pierwiastki dodatnie?
Powierzchnia boczna walca o objętości 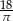 po rozwinięciu jest prostokątem, w którym przekątna tworzy z wysokością walca kąt o mierze
po rozwinięciu jest prostokątem, w którym przekątna tworzy z wysokością walca kąt o mierze 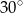 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 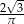 B)
B) 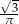 C)
C) 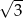 D)
D) 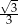
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od jego wysokości. Kąt nachylenia ściany bocznej do podstawy ma miarę
A) 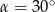 B)
B) 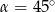 C)
C) 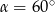 D)
D) 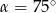
W ciągu geometrycznym pierwszy wyraz 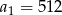 , a iloraz
, a iloraz 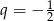 . Ósmy wyraz tego ciągu jest równy
. Ósmy wyraz tego ciągu jest równy
A) -4 B) -2 C) 2 D) 4
Dany jest ciąg geometryczny 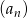 , w którym
, w którym 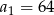 i
i 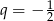 . Wówczas
. Wówczas
A) 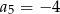 B)
B) 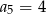 C)
C) 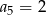 D)
D) 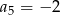
W ciągu geometrycznym pierwszy wyraz 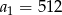 , a iloraz
, a iloraz 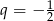 . Siódmy wyraz tego ciągu jest równy
. Siódmy wyraz tego ciągu jest równy
A) -8 B) -4 C) 4 D) 8
W ciągu geometrycznym pierwszy wyraz 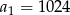 , a iloraz
, a iloraz 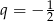 . Dziewiąty wyraz tego ciągu jest równy
. Dziewiąty wyraz tego ciągu jest równy
A) -2 B) -4 C) 4 D) 2
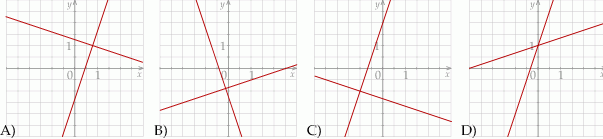
Dany jest układ równań
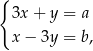
gdzie  i
i 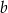 są pewnymi liczbami rzeczywistymi. Na którym z rysunków może być przedstawiona interpretacja geometryczna tego układu równań?
są pewnymi liczbami rzeczywistymi. Na którym z rysunków może być przedstawiona interpretacja geometryczna tego układu równań?
Spośród tych graniastosłupów prawidłowych trójkątnych, których suma długości wszystkich krawędzi jest równa 18, wybierz graniastosłup o największej objętości. Oblicz tę maksymalną objętość.
Suma długości wszystkich krawędzi graniastosłupa prawidłowego sześciokątnego jest równa 36. Jakie są wymiary graniastosłupa o największej objętości?
Jacek bierze udział w olimpiadzie chemicznej i olimpiadzie matematycznej. Prawdopodobieństwo, że zostanie laureatem olimpiady chemicznej jest równe 0,3, a prawdopodobieństwo, że zostanie laureatem przynajmniej jednej z tych dwóch olimpiad wynosi 0,72. Prawdopodobieństwo, że będzie laureatem obu olimpiad jest równe 0,18. Zatem prawdopodobieństwo, że będzie laureatem olimpiady matematycznej jest równe
A) 0,1 B) 0,6 C) 0,7 D) 0,4
Ania bierze udział w olimpiadzie biologicznej i olimpiadzie fizycznej. Prawdopodobieństwo, że zostanie laureatką olimpiady biologicznej jest równe 0,4, a prawdopodobieństwo, że zostanie laureatką przynajmniej jednej z tych dwóch olimpiad wynosi 0,62. Prawdopodobieństwo, że będzie laureatką obu olimpiad jest równe 0,18. Zatem prawdopodobieństwo, że będzie laureatką olimpiady fizycznej jest równe
A) 0,4 B) 0,3 C) 0,5 D) 0,2
Tomek bierze udział w olimpiadzie fizycznej i olimpiadzie matematycznej. Prawdopodobieństwo, że zostanie laureatem olimpiady fizycznej jest równe 0,5, a prawdopodobieństwo, że zostanie laureatem przynajmniej jednej z tych dwóch olimpiad wynosi 0,74. Prawdopodobieństwo, że będzie laureatem obu olimpiad jest równe 0,26. Zatem prawdopodobieństwo, że będzie laureatem olimpiady matematycznej jest równe
A) 0,5 B) 0,6 C) 0,7 D) 0,4
Wyznacz wzór funkcji liniowej, wiedząc że jej wykres jest nachylony do osi 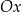 pod kątem
pod kątem 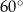 i przechodzi przez punkt
i przechodzi przez punkt 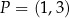 .
.
Zbiorem rozwiązań nierówności 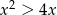 jest
jest
A) 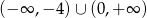 B)
B) 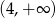 C)
C) 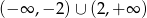 D)
D) 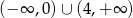
Zbiorem rozwiązań nierówności 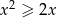 jest:
jest:
A) 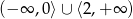 B)
B) 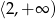 C)
C) 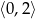 D)
D) 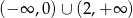
Zbiorem rozwiązań nierówności 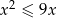 jest przedział
jest przedział
A) 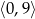 B)
B) 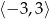 C)
C) 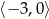 D)
D) 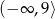
Zbiorem rozwiązań nierówności 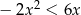 jest
jest
A) 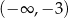 B)
B) 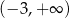 C)
C) 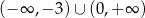 D)
D) 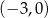
Rozwiązaniem nierówności 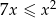 jest zbiór
jest zbiór
A) 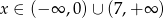 B)
B) 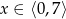 C)
C) 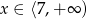 D)
D) 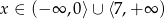
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 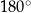 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 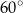 B)
B) 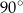 C)
C) 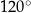 D)
D) 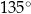
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 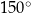 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 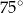 B)
B) 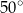 C)
C) 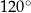 D)
D) 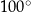
Kąt środkowy i kąt wpisany w okrąg są oparte na tym samym łuku. Suma ich miar jest równa 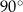 . Miara kata środkowego jest równa
. Miara kata środkowego jest równa
A) 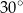 B)
B) 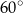 C)
C) 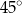 D)
D) 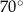
W okręgu 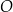 kąt środkowy
kąt środkowy 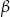 oraz kąt wpisany
oraz kąt wpisany  są oparte na tym samym łuku. Kąt
są oparte na tym samym łuku. Kąt 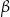 ma miarę o
ma miarę o 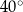 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 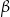 jest równa
jest równa
A) 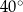 B)
B) 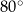 C)
C) 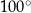 D)
D) 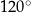
W okręgu 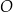 kąt środkowy
kąt środkowy 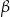 oraz kąt wpisany
oraz kąt wpisany  są oparte na tym samym łuku. Kąt
są oparte na tym samym łuku. Kąt 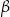 ma miarę o
ma miarę o 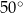 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 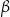 jest równa
jest równa
A) 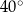 B)
B) 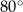 C)
C) 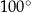 D)
D) 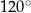
Miara kąta wpisanego w okrąg jest o 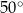 mniejsza od miary kąta środkowego opartego na tym samym łuku. Zatem miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Zatem miara kąta wpisanego jest równa
A) 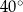 B)
B) 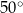 C)
C) 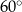 D)
D) 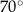
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 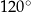 . Jaka jest miara kąta środkowego?
. Jaka jest miara kąta środkowego?
A) 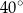 B)
B) 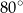 C)
C) 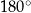 D)
D) 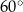
Miara kąta wpisanego w okrąg jest o 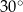 mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
A) 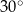 B)
B) 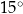 C)
C) 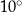 D)
D) 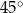
Miara kąta wpisanego w okrąg jest o 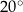 mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
A) 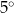 B)
B) 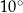 C)
C) 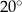 D)
D) 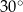
Suma kwadratów długości trzech boków trójkąta prostokątnego jest równa 162. Zatem przeciwprostokątna może mieć długość:
A) 12 B) 81 C) 54 D) 9
Suma kwadratów długości trzech boków trójkąta prostokątnego jest równa 98. Zatem przeciwprostokątna ma długość:
A) 49 B) 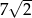 C) 7 D) 9
C) 7 D) 9
Samochód przebył w pewnym czasie 210 km. Gdyby jechał ze średnią prędkością o 10 km/h większą, to czas przejazdu skróciłby się o pół godziny. Oblicz, z jaką średnią prędkością jechał ten samochód.
Rowerzysta wybrał się na wycieczkę nad jezioro i z powrotem. W obie strony jechał dokładnie tą samą trasą i łącznie pokonał 80 km. Jadąc z domu nad jezioro poruszał się z prędkością o 4 km/h mniejszą niż w drodze powrotnej i pokonał trasę w czasie o 20 minut dłuższym niż trasę powrotną. Z jaką prędkością jechał rowerzysta w drodze powrotnej i ile czasu zajął mu powrót do domu znad jeziora?
Rowerzysta wybrał się na wycieczkę nad jezioro i z powrotem. W obie strony jechał dokładnie tą samą trasą i łącznie pokonał 60 km. Jadąc z domu nad jezioro poruszał się z prędkością o 2 km/h większą niż w drodze powrotnej i pokonał trasę w czasie o 10 minut krótszym niż trasę powrotną. Z jaką prędkością jechał rowerzysta w drodze powrotnej i ile czasu zajął mu powrót do domu znad jeziora?
Kolarz przejechał trasę długości 60 km. Gdyby jechał ze średnią prędkością większą o 1 km/h, to przejechałby tę trasę w czasie o 6 minut krótszym. Oblicz, z jaką średnią prędkością jechał ten kolarz.
Oblicz, z jaką średnią prędkością autobus przejechał odległość 120 km, wiedząc, że gdyby jechał z prędkością średnią o 10 km/h większą, to czas przejazdu byłby krótszy o 24 minut.
Grupa rowerzystów jechała ze stałą prędkością do miasta oddalonego o 120 km. Gdyby jechali ze średnią prędkością o 5 km/godz. większą, to przejechaliby tę odległość w czasie o 2 godziny krótszym. Wyznacz średnią prędkość grupy i czas przejazdu.
Pewien kierowca, jadąc z miasta 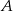 do miasta
do miasta 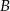 , zmierzył czas i prędkość jazdy. Drogę powrotną pokonał z prędkością o 12 km/h większą, w czasie o 12 minut krótszym. Z jaką średnią prędkością wracał kierowca do miasta
, zmierzył czas i prędkość jazdy. Drogę powrotną pokonał z prędkością o 12 km/h większą, w czasie o 12 minut krótszym. Z jaką średnią prędkością wracał kierowca do miasta 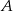 , jeżeli wiadomo, że miasta te są oddalone od siebie o 117 km?
, jeżeli wiadomo, że miasta te są oddalone od siebie o 117 km?
Kolarz pokonał trasę 114 km. Gdyby jechał ze średnią prędkością mniejszą o 9,5 km/h, to pokonałby tę trasę w czasie o 2 godziny dłuższym. Oblicz, z jaką średnią prędkością jechał ten kolarz.
Oblicz, z jaką średnią prędkością autobus przejechał odległość 120 km, wiedząc, że gdyby jechał z prędkością średnią o 10 km/h większą, to czas przejazdu byłby krótszy o 36 minut.
Kierowca obliczył, że trasę 220 km pokona w czasie 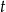 , jeśli będzie jechał ze średnią prędkością
, jeśli będzie jechał ze średnią prędkością  . Wyjechał o 20 minut później niż zamierzał, więc aby dojechać na zaplanowaną godzinę, musiał zwiększyć prędkość o 5 km/h. Oblicz średnią prędkość z jaką planował jechać kierowca.
. Wyjechał o 20 minut później niż zamierzał, więc aby dojechać na zaplanowaną godzinę, musiał zwiększyć prędkość o 5 km/h. Oblicz średnią prędkość z jaką planował jechać kierowca.
Samochód przejechał trasę długości 84 km. Gdyby jechał ze średnią prędkością większą o 12 km/h, to przejechałby tę trasę w czasie o 21 minut krótszym. Oblicz, z jaką średnią prędkością jechał ten samochód.
Samochód przebył w pewnym czasie 210 km. Gdyby jechał o pół godziny krócej to średnia prędkość z jaką przejechał tę trasę byłaby większa o 10 km/h. Oblicz, z jaką średnią prędkością jechał ten samochód.
Turysta przeszedł trasę długości 24 km ze stałą prędkością. Gdyby prędkość tę zwiększył o 1,2 km/h, to tę samą drogę przeszedłby w czasie o 1 godzinę krótszym. Oblicz rzeczywistą prędkość turysty i czas, w którym przebył trasę.
Po zmodernizowaniu linii kolejowych przeciętna prędkość pociągów ekspresowych kursujących na 400-kilometrowej trasie wzrosła o 20 km/godz, a czas podróży skrócił się o godzinę. Oblicz, z jaką średnia prędkością jeżdżą obecnie pociągi ekspresowe na tej trasie.

