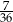Prawdopodobieństwo zdarzenia 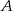 jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 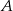 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 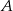 jest równe
jest równe
A) 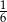 B)
B)  C)
C) 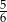 D)
D) 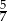
/Szkoła średnia
Jeżeli prawdopodobieństwo zdarzenia losowego 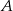 jest 5 razy większe od prawdopodobieństwa zdarzenia przeciwnego do zdarzenia
jest 5 razy większe od prawdopodobieństwa zdarzenia przeciwnego do zdarzenia 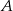 , to prawdopodobieństwo zdarzenia
, to prawdopodobieństwo zdarzenia 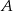 jest równe
jest równe
A) 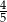 B)
B) 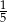 C)
C) 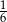 D)
D) 
Prawdopodobieństwo zdarzenia 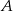 jest 7 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do
jest 7 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do 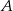 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 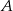 jest równe
jest równe
A)  B)
B)  C)
C) 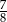 D)
D) 
Jeżeli 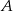 jest zdarzeniem losowym oraz
jest zdarzeniem losowym oraz 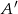 jest zdarzeniem przeciwnym do zdarzenia
jest zdarzeniem przeciwnym do zdarzenia 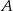 i
i 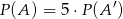 , to prawdopodobieństwo zdarzenia
, to prawdopodobieństwo zdarzenia 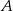 jest równe
jest równe
A) 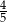 B)
B) 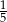 C)
C) 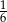 D)
D) 
Jeżeli 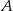 jest zdarzeniem losowym, a
jest zdarzeniem losowym, a 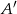 – zdarzeniem przeciwnym do zdarzenia
– zdarzeniem przeciwnym do zdarzenia 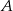 oraz zachodzi równość
oraz zachodzi równość 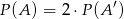 , to
, to
A) 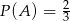 B)
B) 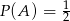 C)
C) 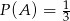 D)
D) 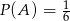
Prawdopodobieństwo zdarzenia 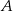 jest 5 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 5 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 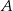 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 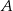 jest równe
jest równe
A)  B)
B) 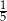 C)
C)  D)
D) 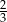
Prawdopodobieństwo zdarzenia 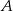 jest 6 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do
jest 6 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do 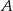 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 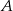 jest równe
jest równe
A) 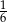 B)
B)  C)
C) 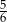 D)
D) 
Prawdopodobieństwo zdarzenia 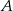 jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 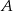 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 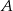 jest równe
jest równe
A) 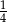 B)
B) 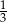 C)
C) 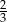 D)
D) 
Naszkicuj wykres funkcji 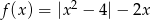 . Określ liczbę rozwiązań równania
. Określ liczbę rozwiązań równania 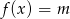 w zależności od wartości parametru
w zależności od wartości parametru 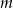 .
.
Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 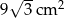 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 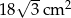 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 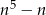 jest podzielna przez 5.
jest podzielna przez 5.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 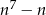 jest podzielna przez 7.
jest podzielna przez 7.
Oblicz prawdopodobieństwo warunkowe, że w czterokrotnym rzucie symetryczną sześcienną kostką do gry otrzymamy co najmniej jedną „czwórkę”, pod warunkiem że otrzymamy co najmniej jedną „piątkę”.
Pole rombu jest równe 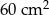 . Dłuższa przekątna rombu podzieliła kąt ostry rombu na takie dwa kąty o mierze
. Dłuższa przekątna rombu podzieliła kąt ostry rombu na takie dwa kąty o mierze  , że
, że 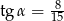 . Oblicz długość boku rombu.
. Oblicz długość boku rombu.
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 8 cm, a jego wysokość 12 cm. Połączono środki dwóch sąsiednich krawędzi dolnej podstawy oraz najbardziej odległy od tego odcinka wierzchołek górnej podstawy. Oblicz pole otrzymanego trójkąta.
Wykaż, że jeżeli 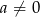 i
i 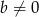 , to
, to 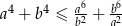 .
.
Rozwiąż nierówność
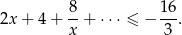
Rozwiąż nierówność, której lewa strona jest sumą szeregu geometrycznego
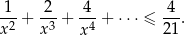
Wartość wyrażenia 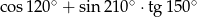 jest równa
jest równa
A) 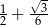 B)
B) 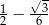 C)
C) 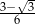 D)
D) 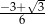
Wartość wyrażenia 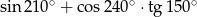 jest równa
jest równa
A) 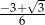 B)
B) 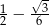 C)
C) 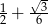 D)
D) 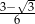
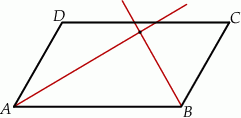
Uzasadnij, że dwusieczne dwóch sąsiednich kątów równoległoboku przecinają się pod kątem prostym.
Uzasadnij, że dwusieczne kątów 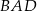 i
i 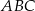 równoległoboku
równoległoboku 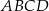 są prostopadłe.
są prostopadłe.
Dwa krótsze boki trójkąta rozwartokątnego mają długości 5 cm i 6 cm. Jakie wartości może przyjmować długość trzeciego boku trójkąta?
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 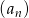 wyraża się wzorem
wyraża się wzorem 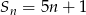 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz ciągu
-ty wyraz ciągu 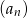 dla
dla 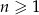 .
.
W ciągu arytmetycznym 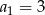 oraz
oraz 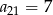 . Wtedy suma
. Wtedy suma 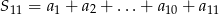 jest równa
jest równa
A) 44 B) 88 C) 46 D) 55
Odcinek 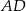 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 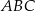 , w którym
, w którym 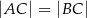 . Udowodnij, że
. Udowodnij, że 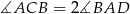 .
.
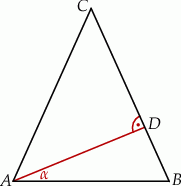
Wykaż, że miara kąta między wysokością trójkąta równoramiennego poprowadzoną do ramienia a podstawą tego trójkąta jest dwa razy mniejsza od miary kąta zawartego między ramionami tego trójkąta.
Z trójkąta 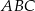 o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat  o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
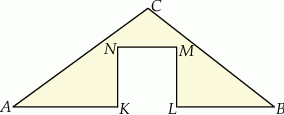
A) 64 B) 60 C) 75 D) 70
Na bokach 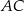 i
i 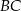 trójkąta
trójkąta 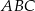 wybrano odpowiednio punkty
wybrano odpowiednio punkty 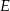 i
i  w ten sposób, że
w ten sposób, że 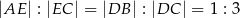 . Punkt
. Punkt  jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 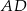 i
i 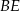 (zobacz rysunek).
(zobacz rysunek).
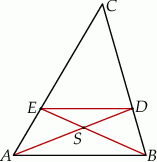
Oblicz pole trójkąta 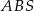 jeżeli pole trójkąta
jeżeli pole trójkąta 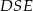 równe 36.
równe 36.
Rozwiąż równanie 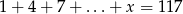 , w którym lewa strona jest sumą kolejnych wyrazów ciągu arytmetycznego.
, w którym lewa strona jest sumą kolejnych wyrazów ciągu arytmetycznego.
W trójkąt równoramienny 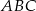 , w którym
, w którym 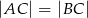 ,
, 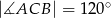 , wpisano okrąg, którego promień ma długość
, wpisano okrąg, którego promień ma długość  . Oblicz długości boków trójkąta.
. Oblicz długości boków trójkąta.
Doświadczenie losowe polega na czterokrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą nieparzystą, jest równe
A) 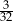 B)
B) 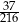 C)
C) 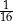 D)
D)