Zbiorem wartości funkcji 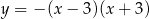 określonej dla
określonej dla 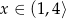 jest przedział
jest przedział
A) 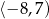 B)
B) 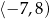 C)
C) 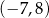 D)
D) 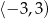
/Szkoła średnia
Zbiorem wartości funkcji 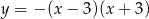 określonej dla
określonej dla 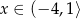 jest przedział
jest przedział
A) 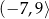 B)
B) 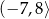 C)
C) 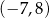 D)
D) 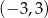
Wykaż, że jeżeli  i
i 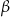 są kątami ostrymi, dla których
są kątami ostrymi, dla których 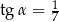 i
i 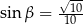 , to
, to 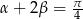 .
.
Pole figury ograniczonej fragmentem wykresu funkcji 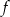 danej wzorem
danej wzorem 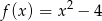 i osią
i osią 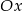 jest
jest
A) mniejsze od 8 B) większe od 8 C) równe 8 D) większe od 16
Pole figury ograniczonej fragmentem wykresu funkcji 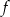 danej wzorem
danej wzorem 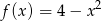 i osią
i osią 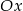 jest
jest
A) mniejsze od 16 B) mniejsze od 8 C) równe 16 D) większe od 16
Pole figury ograniczonej fragmentem wykresu funkcji 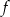 danej wzorem
danej wzorem 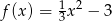 i osią
i osią 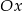 jest
jest
A) mniejsze od 9 B) równe 18 C) większe od 9 D) większe od 18
Punkt 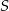 jest środkiem okręgu wpisanego w trapez
jest środkiem okręgu wpisanego w trapez 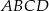 (
(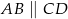 ). Wykaż, że trójkąt
). Wykaż, że trójkąt 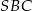 jest prostokątny.
jest prostokątny.
Ósmy wyraz ciągu 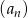 o wyrazie ogólnym
o wyrazie ogólnym 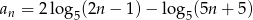 , gdzie
, gdzie 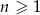 jest równy
jest równy
A) 1 B) 5 C) -1 D) -5
Siódmy wyraz ciągu 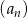 o wyrazie ogólnym
o wyrazie ogólnym 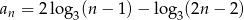 , gdzie
, gdzie 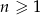 jest równy
jest równy
A) 1 B) 2 C) -1 D) -2
Na bokach trójkąta równobocznego zbudowano dwa kwadraty w sposób pokazany na rysunku.
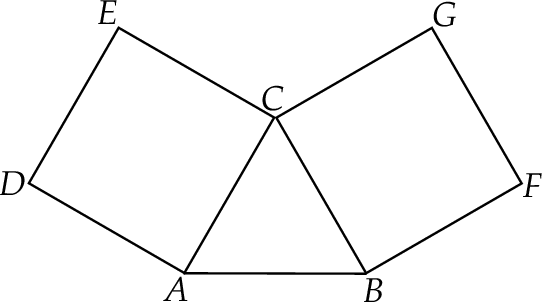
Wykaż, że punkty 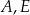 i
i 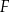 są wierzchołkami trójkąta prostokątnego.
są wierzchołkami trójkąta prostokątnego.
Dany jest okrąg o środku w punkcie 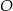 . Prosta
. Prosta 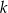 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 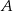 .
.
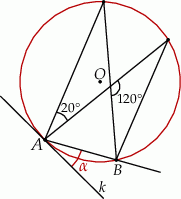
Miara kąta  jest równa
jest równa
A) 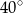 B)
B) 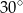 C)
C) 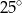 D)
D) 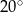
Dany jest okrąg o środku w punkcie 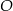 . Prosta
. Prosta 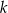 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 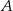 .
.
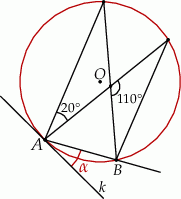
Miara kąta  jest równa
jest równa
A) 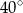 B)
B) 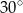 C)
C) 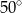 D)
D) 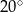
Przyprostokątne trójkąta prostokątnego 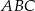 mają długości 10 i 24. Przeciwprostokątna trójkąta
mają długości 10 i 24. Przeciwprostokątna trójkąta 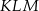 podobnego do niego ma długość 39. Oblicz pole trójkąta
podobnego do niego ma długość 39. Oblicz pole trójkąta 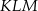 .
.
Trójkąty prostokątne 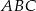 i
i 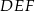 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 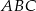 mają długości 5 i 12, a przeciwprostokątna trójkąta
mają długości 5 i 12, a przeciwprostokątna trójkąta 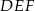 ma długość 26. Wyznacz pole trójkąta
ma długość 26. Wyznacz pole trójkąta 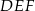 .
.
Przyprostokątne trójkąta prostokątnego 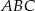 mają długości 9 i 40. Najdłuższy bok tego trójkąta jest równy najkrótszemu bokowi trójkąta
mają długości 9 i 40. Najdłuższy bok tego trójkąta jest równy najkrótszemu bokowi trójkąta 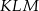 podobnego do trójkąta
podobnego do trójkąta 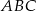 . Oblicz pole trójkąta
. Oblicz pole trójkąta 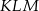 .
.
Rozwiąż równanie 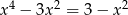 .
.
Rozwiąż równanie 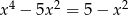 .
.
Przeciwległe wierzchołki kwadratu mają współrzędne 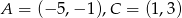 . Promień okręgu wpisanego w ten kwadrat jest równy
. Promień okręgu wpisanego w ten kwadrat jest równy
A) 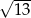 B)
B) 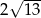 C)
C) 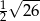 D)
D) 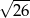
Przeciwległe wierzchołki kwadratu mają współrzędne 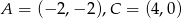 . Promień okręgu wpisanego w ten kwadrat jest równy
. Promień okręgu wpisanego w ten kwadrat jest równy
A) 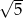 B)
B) 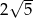 C)
C) 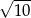 D)
D) 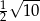
Przeciwległe wierzchołki kwadratu mają współrzędne 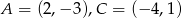 . Średnica okręgu wpisanego w ten kwadrat jest równa
. Średnica okręgu wpisanego w ten kwadrat jest równa
A) 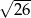 B)
B) 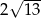 C)
C) 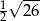 D)
D) 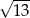
Przeciwległe wierzchołki kwadratu mają współrzędne 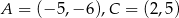 . Promień okręgu wpisanego w ten kwadrat jest równy
. Promień okręgu wpisanego w ten kwadrat jest równy
A) 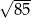 B)
B) 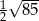 C)
C) 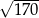 D)
D) 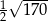
Ze zbioru liczb 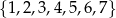 losujemy kolejno bez zwracania dwie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3, jeżeli pierwsza z wylosowanych liczb jest liczbą pierwszą.
losujemy kolejno bez zwracania dwie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3, jeżeli pierwsza z wylosowanych liczb jest liczbą pierwszą.
Kąt  jest ostry i
jest ostry i 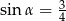 . Wartość wyrażenia
. Wartość wyrażenia 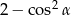 jest równa
jest równa
A) 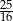 B)
B)  C)
C) 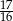 D)
D) 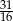
Kąt  jest ostry i
jest ostry i 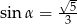 . Wartość wyrażenia
. Wartość wyrażenia 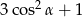 jest równa
jest równa
A)  B)
B) 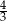 C)
C)  D)
D) 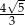
Kąt  jest ostry i
jest ostry i 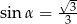 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 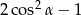 jest równa
jest równa
A) 0 B) 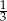 C)
C) 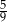 D) 1
D) 1
Kąt  jest ostry i
jest ostry i 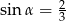 . Wartość wyrażenia
. Wartość wyrażenia 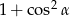 jest równa
jest równa
A) 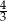 B)
B) 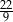 C)
C) 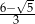 D)
D) 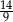
Kąt  jest ostry i
jest ostry i 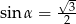 . Wartość wyrażenia
. Wartość wyrażenia 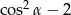 jest równa
jest równa
A) 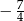 B)
B) 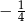 C)
C) 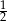 D)
D) 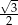
Funkcja 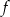 określona jest wzorem
określona jest wzorem 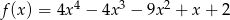 .
.
- Znajdź punkt przecięcia wykresu funkcji
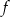 z osia
z osia 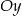 .
. - Znajdź, o ile istnieją, punkty przecięcia funkcji
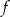 z osia
z osia 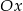 .
. - Wyznacz te argumenty, dla których funkcje
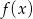 i funkcja
i funkcja 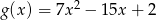 przyjmują tę samą wartość.
przyjmują tę samą wartość.
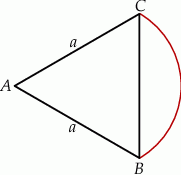
Trójkąt 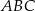 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Wykaż, że łuk okręgu opisanego na tym trójkącie zawarty między wierzchołkami
. Wykaż, że łuk okręgu opisanego na tym trójkącie zawarty między wierzchołkami 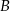 i
i 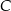 ma długość większą niż
ma długość większą niż 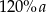 .
.
Trójkąt 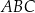 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Wykaż, że łuk okręgu wpisanego w ten trójkąt zawarty między dwoma kolejnymi punktami styczności tego okręgu z bokami trójkąta ma długość większą niż
. Wykaż, że łuk okręgu wpisanego w ten trójkąt zawarty między dwoma kolejnymi punktami styczności tego okręgu z bokami trójkąta ma długość większą niż 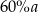 .
.

Z punktu 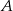 leżącego na okręgu poprowadź cięciwę
leżącego na okręgu poprowadź cięciwę 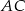 o długości równej promieniowi okręgu oraz średnicę
o długości równej promieniowi okręgu oraz średnicę 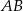 . Wyznacz miary kątów wewnętrznych trójkąta
. Wyznacz miary kątów wewnętrznych trójkąta 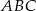 .
.
Liczby 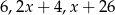 w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę
w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę  tego ciągu.
tego ciągu.
Liczby 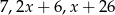 w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę
w podanej kolejności są pierwszym, drugim i trzecim wyrazem pewnego ciągu arytmetycznego. Oblicz różnicę  tego ciągu.
tego ciągu.
Z prostokąta 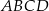 o polu 30 wycięto trójkąt
o polu 30 wycięto trójkąt  (tak jak na rysunku). Pole zacieniowanej figury jest równe
(tak jak na rysunku). Pole zacieniowanej figury jest równe
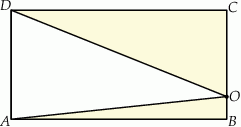
A) 7,5 B) 15 C) 20 D) 25
Z prostokąta  o polu 28 wycięto trójkąt
o polu 28 wycięto trójkąt  , przy czym punkty
, przy czym punkty 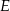 i
i 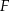 są środkami odpowiednio boków
są środkami odpowiednio boków 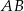 i
i 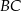 .
.
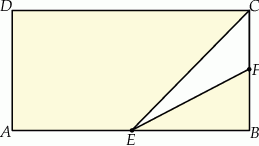
Pole zacieniowanej figury jest równe
A) 3,5 B) 21 C) 25 D) 24,5
Dla jakich wartości parametru 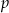 proste
proste 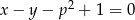 i
i 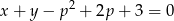 przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach
przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach 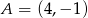 ,
, 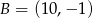 ,
, 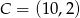 ,
, 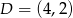 ?
?
Przekątne deltoidu 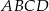 przecinają się w punkcie
przecinają się w punkcie 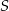 , który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie
, który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie 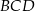 jeżeli okręgi opisane na trójkątach
jeżeli okręgi opisane na trójkątach 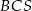 i
i 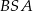 mają odpowiednio równania
mają odpowiednio równania 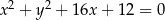 i
i 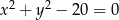 .
.
Wyznacz wszystkie wartości parametru 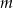 , dla których prosta o równaniu
, dla których prosta o równaniu 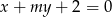 ma dokładnie dwa punkty wspólne z parabolą o równaniu
ma dokładnie dwa punkty wspólne z parabolą o równaniu 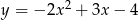 .
.

