Spodnie po obniżce ceny o 30% kosztują 126 zł. Ile kosztowały spodnie przed obniżką?
A) 163,80 zł B) 180 zł C) 294 zł D) 420 zł
/Szkoła średnia
Cena książki wzrosła o 15% i wynosi 92 zł. Ile kosztowała książka przed podwyżką?
A) 105,8 zł B) 77 zł C) 78,2 zł D) 80 zł
Spodnie po obniżce ceny o 25% kosztują 168 zł. Ile kosztowały spodnie przed obniżką?
A) 193 zł B) 210 zł C) 224 zł D) 336 zł
Koszt uczestnictwa w obozie sportowym w 2018 r. wynosi 1620 zł. Wzrósł on w stosunku do kosztu z 2017 r. o 35%. Koszt uczestnictwa w obozie w 2017 r. wynosił
A) 1215 zł B) 1053 zł C) 1200 zł D) 567 zł
Medyczna maseczka ochronna wielokrotnego użytku z wymiennymi filtrami wskutek podwyżki zdrożała o 40% i kosztuje obecnie 106,40 zł. Cena maseczki przed podwyżką była równa
A) 63,84 zł B) 65,40 zł C) 76,00 zł D) 66,40 zł
Cena roweru po obniżce o 15% była równa 850 zł. Przed obniżką ten rower kosztował
A) 865,00 zł B) 850,15 zł C) 1000,00 zł D) 977,50 zł
W trójkącie równoramiennym podstawa 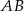 ma długość 8 cm. Promień okręgu, stycznego w punktach
ma długość 8 cm. Promień okręgu, stycznego w punktach 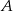 i
i 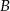 do prostych zawierających ramiona
do prostych zawierających ramiona 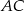 i
i 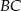 trójkąta, ma długość 5 cm. Oblicz pole trójkąta
trójkąta, ma długość 5 cm. Oblicz pole trójkąta 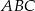 .
.
Ostrosłup ma 12 krawędzi. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 12 B) 9 C) 8 D) 7
Jeśli ostrosłup ma 50 krawędzi, to liczba jego ścian jest równa
A) 50 B) 26 C) 25 D) 22
Ostrosłup, który ma 12 krawędzi, ma
A) 6 ścian B) 7 ścian C) 8 ścian D) 9 ścian
Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa
A) 5 B) 7 C) 8 D) 10
O ile procent pole koła o promieniu długości 8 jest większe od pola koła wyznaczonego przez okrąg o równaniu 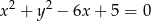 .
.
Dany jest trójkąt 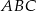 , w którym
, w którym 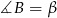 , a kąt zewnętrzny przy wierzchołku
, a kąt zewnętrzny przy wierzchołku 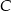 ma miarę
ma miarę  .
.
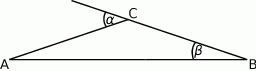
Wykaż, że jeśli 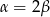 , to trójkąt
, to trójkąt 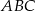 jest równoramienny.
jest równoramienny.
W trapezie 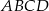 (
(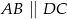 ) przekątne
) przekątne 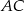 i
i 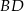 przecinają się w punkcie
przecinają się w punkcie 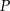 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 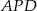 jest równe polu trójkąta
jest równe polu trójkąta 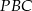 .
.
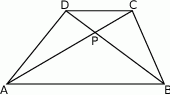
Dane są okręgi o równaniach 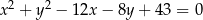 i
i 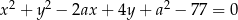 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
Dane są okręgi o równaniach 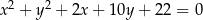 i
i 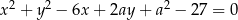 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
Rozwiąż nierówność 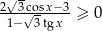 w przedziale
w przedziale 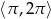 .
.
Środek 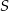 okręgu
okręgu 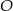 należy do prostej
należy do prostej 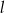 o równaniu
o równaniu 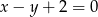 . Punkty
. Punkty 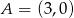 i
i 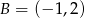 należą do tego okręgu.
należą do tego okręgu.
- Wyznacz równanie okręgu
 .
. - Wyznacz współrzędne takiego punktu
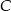 należącego do okręgu
należącego do okręgu 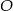 , że
, że 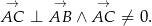
- Wyznacz równania stycznych
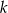 i
i 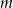 do okręgu
do okręgu 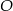 takich, że
takich, że 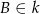 i
i 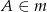 oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
Przekątne trapezu 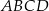 przecinają się w punkcie
przecinają się w punkcie 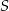 w ten sposób, że
w ten sposób, że 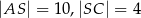 ,
, 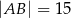 .
.
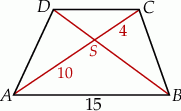
Długość odcinka 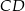 jest równa
jest równa
A) 4 B) 6 C) 8 D) 9
W stożek o promieniu  i wysokości
i wysokości 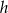 wpisujemy graniastosłupy sześciokątne prawidłowe tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Podaj wymiary graniastosłupa o największym polu powierzchni bocznej.
wpisujemy graniastosłupy sześciokątne prawidłowe tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Podaj wymiary graniastosłupa o największym polu powierzchni bocznej.
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
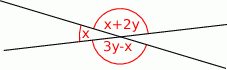
A) 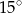 B)
B) 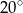 C)
C) 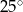 D)
D) 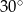
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
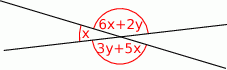
A) 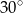 B)
B) 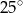 C)
C) 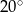 D)
D) 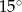
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
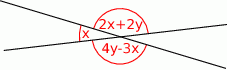
A) 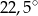 B)
B) 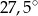 C)
C) 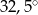 D)
D) 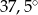
Funkcja homograficzna 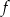 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 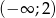 i
i 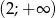 . Zbiór
. Zbiór 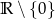 jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
- Znajdź wzór funkcji
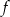 .
. - Naszkicuj wykres funkcji
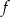 .
. - Uzasadnij, że funkcja
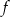 nie jest monotoniczna w zbiorze
nie jest monotoniczna w zbiorze 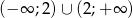 .
.
Liczby rzeczywiste 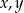 spełniają warunki:
spełniają warunki: 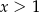 ,
, 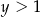 oraz
oraz 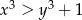 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość
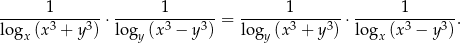
Wartość wyrażenia 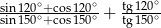 jest równa
jest równa
A) 4 B) 0 C) 1 D) 2
Podstawą ostrosłupa jest kwadrat 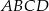 o boku długości 40. Pola ścian bocznych
o boku długości 40. Pola ścian bocznych 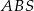 ,
, 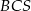 ,
, 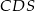 i
i 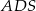 są odpowiednio równe: 740,
są odpowiednio równe: 740, 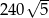 , 260 i 400. Oblicz objętość tego ostrosłupa.
, 260 i 400. Oblicz objętość tego ostrosłupa.
Przyprostokątna 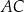 trójkąta prostokątnego
trójkąta prostokątnego 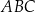 ma długość 8 oraz
ma długość 8 oraz 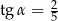 (zobacz rysunek).
(zobacz rysunek).
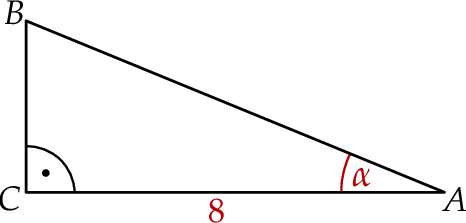
Pole tego trójkąta jest równe
A) 12 B) 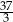 C)
C) 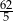 D)
D) 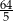
Przyprostokątna 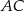 trójkąta prostokątnego
trójkąta prostokątnego 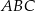 ma długość 14 oraz
ma długość 14 oraz 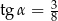 (zobacz rysunek).
(zobacz rysunek).
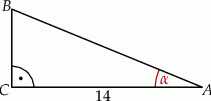
Pole tego trójkąta jest równe
A) 73,5 B) 36,75 C) 5,25 D) 37,3
Wyznacz odległość punktu 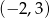 od prostej o równaniu
od prostej o równaniu 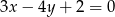 .
.
Ile jest liczb naturalnych trzycyfrowych, których iloczyn cyfr jest równy 0?
A) 162 B) 90 C) 171 D) 172
Ile jest liczb naturalnych czterocyfrowych o różnych cyfrach, których iloczyn cyfr jest równy 0?
A) 1728 B) 504 C) 720 D) 1512
W urnie znajduje się 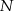 losów, przy czym
losów, przy czym 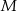 z nich to losy wygrywające (
z nich to losy wygrywające (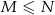 ). Wybieramy losowo
). Wybieramy losowo  losów z urny (
losów z urny (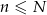 ) i niech
) i niech 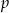 oznacza prawdopodobieństwo, że dokładnie
oznacza prawdopodobieństwo, że dokładnie 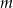 spośród tych losów to losy wygrywające (
spośród tych losów to losy wygrywające (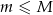 oraz
oraz 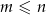 ). Uzasadnij, że
). Uzasadnij, że