W stożek o promieniu  i wysokości
i wysokości 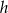 wpisujemy graniastosłupy sześciokątne prawidłowe tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Podaj wymiary graniastosłupa o największym polu powierzchni bocznej.
wpisujemy graniastosłupy sześciokątne prawidłowe tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Podaj wymiary graniastosłupa o największym polu powierzchni bocznej.
/Szkoła średnia
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
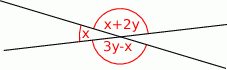
A) 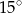 B)
B) 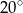 C)
C) 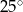 D)
D) 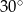
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
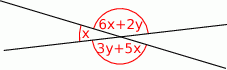
A) 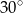 B)
B) 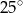 C)
C) 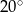 D)
D) 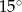
Miara kąta ostrego przecięcia prostych przedstawionych na rysunku wynosi
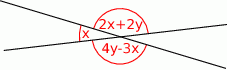
A) 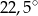 B)
B) 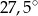 C)
C) 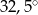 D)
D) 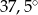
Funkcja homograficzna 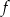 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 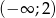 i
i 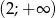 . Zbiór
. Zbiór 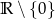 jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
- Znajdź wzór funkcji
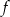 .
. - Naszkicuj wykres funkcji
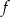 .
. - Uzasadnij, że funkcja
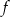 nie jest monotoniczna w zbiorze
nie jest monotoniczna w zbiorze 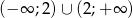 .
.
Liczby rzeczywiste 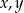 spełniają warunki:
spełniają warunki: 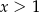 ,
, 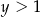 oraz
oraz 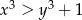 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość
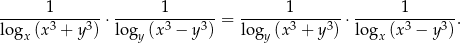
Wartość wyrażenia 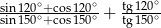 jest równa
jest równa
A) 4 B) 0 C) 1 D) 2
Podstawą ostrosłupa jest kwadrat 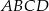 o boku długości 40. Pola ścian bocznych
o boku długości 40. Pola ścian bocznych 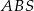 ,
, 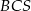 ,
, 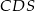 i
i 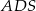 są odpowiednio równe: 740,
są odpowiednio równe: 740, 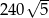 , 260 i 400. Oblicz objętość tego ostrosłupa.
, 260 i 400. Oblicz objętość tego ostrosłupa.
Przyprostokątna 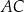 trójkąta prostokątnego
trójkąta prostokątnego 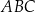 ma długość 8 oraz
ma długość 8 oraz 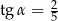 (zobacz rysunek).
(zobacz rysunek).
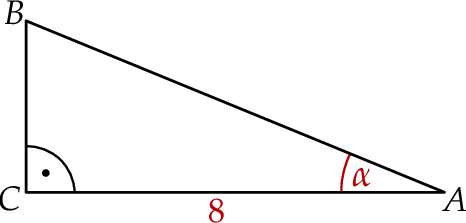
Pole tego trójkąta jest równe
A) 12 B) 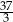 C)
C) 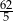 D)
D) 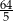
Przyprostokątna 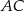 trójkąta prostokątnego
trójkąta prostokątnego 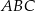 ma długość 14 oraz
ma długość 14 oraz 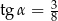 (zobacz rysunek).
(zobacz rysunek).
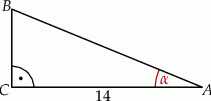
Pole tego trójkąta jest równe
A) 73,5 B) 36,75 C) 5,25 D) 37,3
Wyznacz odległość punktu 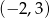 od prostej o równaniu
od prostej o równaniu 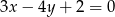 .
.
Ile jest liczb naturalnych trzycyfrowych, których iloczyn cyfr jest równy 0?
A) 162 B) 90 C) 171 D) 172
Ile jest liczb naturalnych czterocyfrowych o różnych cyfrach, których iloczyn cyfr jest równy 0?
A) 1728 B) 504 C) 720 D) 1512
W urnie znajduje się 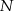 losów, przy czym
losów, przy czym 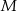 z nich to losy wygrywające (
z nich to losy wygrywające (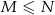 ). Wybieramy losowo
). Wybieramy losowo  losów z urny (
losów z urny (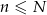 ) i niech
) i niech 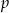 oznacza prawdopodobieństwo, że dokładnie
oznacza prawdopodobieństwo, że dokładnie 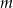 spośród tych losów to losy wygrywające (
spośród tych losów to losy wygrywające (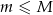 oraz
oraz 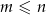 ). Uzasadnij, że
). Uzasadnij, że
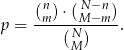
Prosta o równaniu 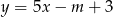 przechodzi przez punkt
przechodzi przez punkt 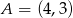 . Wtedy
. Wtedy
A) 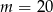 B)
B) 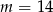 C)
C) 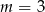 D)
D) 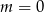
Prosta o równaniu 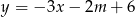 przechodzi przez punkt
przechodzi przez punkt 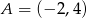 . Wtedy
. Wtedy
A) 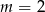 B)
B) 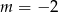 C)
C) 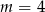 D)
D) 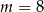
Prosta o równaniu 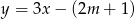 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 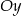 w punkcie
w punkcie 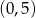 . Wtedy
. Wtedy
A) 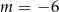 B)
B) 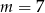 C)
C) 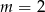 D)
D) 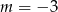
Prosta o równaniu 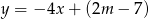 przechodzi przez punkt
przechodzi przez punkt 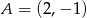 . Wtedy
. Wtedy
A) 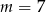 B)
B) 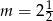 C)
C) 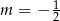 D)
D) 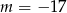
Prosta o równaniu 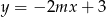 przechodzi przez punkt
przechodzi przez punkt 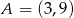 . Wtedy
. Wtedy
A) 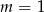 B)
B) 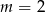 C)
C) 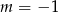 D)
D) 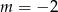
Punkt o współrzędnych 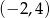 należy do prostej
należy do prostej 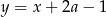 . Zatem
. Zatem
A) 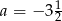 B)
B) 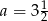 C)
C) 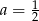 D)
D) 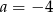
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 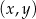 , dana jest prosta
, dana jest prosta 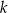 o równaniu
o równaniu 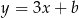 , przechodząca przez punkt
, przechodząca przez punkt 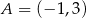 . Współczynnik
. Współczynnik 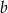 w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 0 B) 6 C) 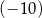 D) 8
D) 8
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 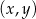 , dana jest prosta
, dana jest prosta 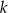 o równaniu
o równaniu 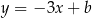 , przechodząca przez punkt
, przechodząca przez punkt 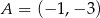 . Współczynnik
. Współczynnik 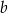 w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 0 B) 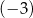 C)
C) 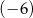 D)
D) 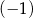
Prosta o równaniu 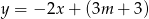 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 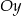 w punkcie
w punkcie 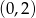 . Wtedy
. Wtedy
A) 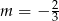 B)
B) 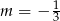 C)
C) 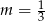 D)
D) 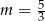
Prosta o równaniu 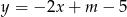 przechodzi przez punkt
przechodzi przez punkt 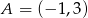 . Wtedy
. Wtedy
A) 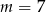 B)
B) 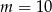 C)
C) 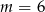 D)
D) 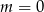
Liczby 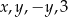 są kolejnymi wyrazami pewnego ciągu arytmetycznego. Znajdź liczbę
są kolejnymi wyrazami pewnego ciągu arytmetycznego. Znajdź liczbę  .
.
Ciąg 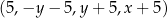 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
Punkty 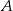 ,
, 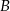 ,
, 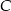 dzielą okrąg na trzy łuki, których stosunek długości wynosi
dzielą okrąg na trzy łuki, których stosunek długości wynosi 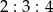 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 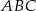 .
.
Punkty 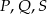 dzielą okrąg na trzy łuki
dzielą okrąg na trzy łuki 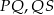 i
i 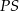 . Długości łuków
. Długości łuków 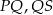 i
i 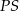 pozostają w stosunku 1:2:3. Oblicz miary kątów trójkąta
pozostają w stosunku 1:2:3. Oblicz miary kątów trójkąta 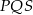 .
.
Punkty 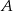 ,
, 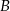 ,
, 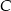 dzielą okrąg na trzy łuki, których stosunek długości wynosi
dzielą okrąg na trzy łuki, których stosunek długości wynosi 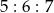 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 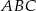 .
.
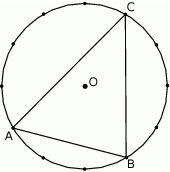
Punkty 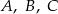 leżą na okręgu o środku
leżą na okręgu o środku 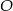 i dzielą ten okrąg na trzy łuki, których stosunek długości jest równy 3:4:5. Oblicz miary kątów trójkąta
i dzielą ten okrąg na trzy łuki, których stosunek długości jest równy 3:4:5. Oblicz miary kątów trójkąta 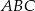 .
.
Dany jest trójkąt równoramienny 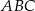 , w którym
, w którym 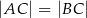 . Na ramieniu
. Na ramieniu 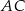 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 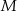 (
(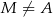 i
i 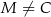 ), a na ramieniu
), a na ramieniu 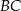 wybrano punkt
wybrano punkt 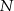 , w taki sposób, że
, w taki sposób, że 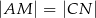 . Przez punkty
. Przez punkty 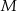 i
i 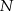 poprowadzono proste prostopadłe do podstawy
poprowadzono proste prostopadłe do podstawy 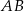 tego trójkąta, które wyznaczają na niej punkty
tego trójkąta, które wyznaczają na niej punkty 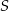 i
i 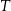 . Udowodnij, że
. Udowodnij, że 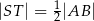 .
.
Dany jest trójkąt równoramienny 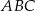 , w którym
, w którym 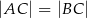 . Na ramieniu
. Na ramieniu 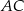 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 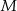 (
(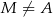 i
i 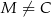 ), a na ramieniu
), a na ramieniu 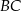 wybrano punkt
wybrano punkt 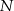 . Przez punkty
. Przez punkty 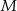 i
i 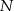 poprowadzono proste prostopadłe do podstawy
poprowadzono proste prostopadłe do podstawy 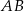 tego trójkąta, które wyznaczają na niej punkty
tego trójkąta, które wyznaczają na niej punkty 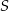 i
i 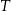 . Wykaż, że jeżeli
. Wykaż, że jeżeli 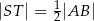 , to
, to 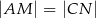 .
.
Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 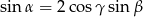 to trójkąt ten jest równoramienny.
to trójkąt ten jest równoramienny.
Wielomian 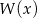 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 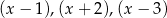 daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian
daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 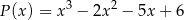 .
.
Przy dzieleniu wielomianu 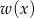 przez dwumian
przez dwumian 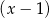 otrzymujemy resztę
otrzymujemy resztę 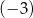 , przy dzieleniu przez dwumian
, przy dzieleniu przez dwumian 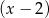 resztę 6, a przy dzieleniu przez dwumian
resztę 6, a przy dzieleniu przez dwumian 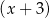 resztę 1. Wyznacz resztę z dzielenia wielomianu
resztę 1. Wyznacz resztę z dzielenia wielomianu 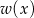 przez wielomian
przez wielomian 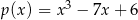 .
.
Wyznacz resztę 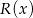 z dzielenia wielomianu
z dzielenia wielomianu 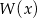 przez wielomian
przez wielomian 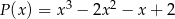 wiedząc, że
wiedząc, że 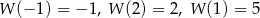 .
.
Dane są funkcje 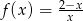 i
i 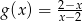 .
.
- Naszkicuj wykresy obu funkcji w jednym układzie współrzędnych.
- Określ przedziały monotoniczności obu funkcji.
- Podaj zbiór rozwiązań nierówności
 .
.
Podstawą ostrosłupa 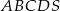 jest kwadrat
jest kwadrat 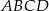 o boku długości 4. Odcinek
o boku długości 4. Odcinek 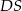 jest wysokością ostrosłupa i ma długość 6. Punkt
jest wysokością ostrosłupa i ma długość 6. Punkt 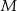 jest środkiem odcinka
jest środkiem odcinka 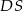 . Oblicz pole przekroju ostrosłupa płaszczyzną
. Oblicz pole przekroju ostrosłupa płaszczyzną 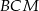 .
.
Osią symetrii paraboli będącej wykresem funkcji 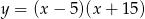 jest prosta o równaniu
jest prosta o równaniu
A) 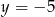 B)
B) 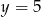 C)
C) 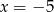 D)
D) 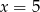
Wykresem funkcji kwadratowej 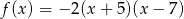 jest parabola której oś symetrii ma równanie
jest parabola której oś symetrii ma równanie
A) 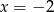 B)
B) 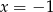 C)
C) 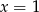 D)
D) 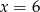
Wykresem funkcji kwadratowej 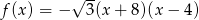 jest parabola której oś symetrii ma równanie
jest parabola której oś symetrii ma równanie
A) 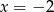 B)
B) 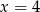 C)
C) 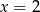 D)
D) 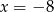
Osią symetrii paraboli będącej wykresem funkcji 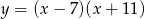 jest prosta o równaniu
jest prosta o równaniu
A) 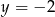 B)
B) 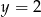 C)
C) 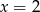 D)
D) 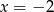
Oś symetrii paraboli, która jest wykresem funkcji 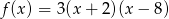 ma równanie
ma równanie
A) 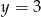 B)
B) 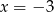 C)
C) 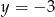 D)
D) 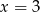
Osią symetrii paraboli określonej wzorem 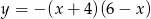 jest prosta o równaniu
jest prosta o równaniu
A) 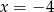 B)
B) 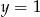 C)
C) 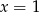 D)
D) 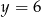
Średnia arytmetyczna trzech liczb: 12, 14, 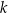 , jest równa 16. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, jest równa 16. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 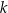 jest równa 22. jest równa 22. | P | F |
Średnia arytmetyczna liczb: 12, 14, 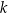 , 11, 17, jest większa od 16. , 11, 17, jest większa od 16. | P | F |

