Wielomian 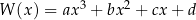 jest iloczynem wielomianów
jest iloczynem wielomianów 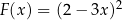 oraz
oraz 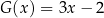 . Oblicz sumę
. Oblicz sumę 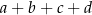 współczynników wielomianu
współczynników wielomianu 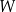 .
.
/Szkoła średnia
W trójkącie 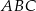 dane są:
dane są: 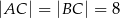 oraz
oraz 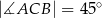 . Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka
. Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka 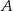 .
.
W trójkącie 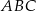 dane są:
dane są: 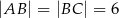 oraz
oraz 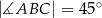 . Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka
. Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka 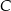 .
.
Rozwiąż równanie 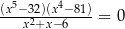 .
.
Prawdopodobieństwo wystąpienia awarii sieci ciepłowniczej na pewnym osiedlu mieszkaniowym w godzinach porannych pojedynczego dnia jest równe 0,1. Oblicz prawdopodobieństwo zdarzenia 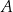 polegającego na tym, że w okresie siedmiu dni wystąpią co najwyżej dwa takie dni, w których nastąpi awaria tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
polegającego na tym, że w okresie siedmiu dni wystąpią co najwyżej dwa takie dni, w których nastąpi awaria tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
Prawdopodobieństwo wystąpienia awarii oświetlenia ulic w pewnym mieście w godzinach wieczornych pojedynczego dnia jest równe 0,2. Oblicz prawdopodobieństwo zdarzenia 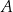 polegającego na tym, że w okresie sześciu dni wystąpią co najwyżej trzy takie dni, w których nastąpi awaria oświetlenia ulic w tym mieście w godzinach wieczornych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
polegającego na tym, że w okresie sześciu dni wystąpią co najwyżej trzy takie dni, w których nastąpi awaria oświetlenia ulic w tym mieście w godzinach wieczornych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
Prawdopodobieństwo wystąpienia awarii sieci ciepłowniczej na pewnym osiedlu mieszkaniowym w godzinach porannych pojedynczego dnia jest równe 0,4. Oblicz prawdopodobieństwo zdarzenia  polegającego na tym, że w okresie dziesięciu dni wystąpi 6, 7 lub 8 awarii tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
polegającego na tym, że w okresie dziesięciu dni wystąpi 6, 7 lub 8 awarii tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
Liczba 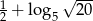 jest równa:
jest równa:
A) 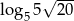 B)
B) 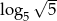 C)
C) 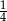 D)
D) 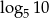
Obliczyć granicę 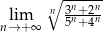 .
.
Wyznacz liczbę rozwiązań równania 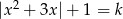 w zależności od parametru
w zależności od parametru 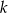 .
.
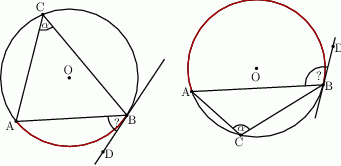
Prosta 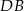 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 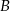 . Oblicz miarę zaznaczonego kąta
. Oblicz miarę zaznaczonego kąta 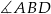 jeśli
jeśli 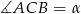 .
.
Suma dwóch liczb jest równa 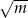 , a ich różnica jest równa
, a ich różnica jest równa 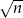 , gdzie
, gdzie 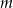 i
i  są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.
są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.
Narysuj wykres funkcji 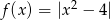 , a następnie wykres funkcji
, a następnie wykres funkcji 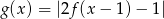 .
.
Spodnie po obniżce ceny o 30% kosztują 126 zł. Ile kosztowały spodnie przed obniżką?
A) 163,80 zł B) 180 zł C) 294 zł D) 420 zł
Spodnie po obniżce ceny o 25% kosztują 168 zł. Ile kosztowały spodnie przed obniżką?
A) 193 zł B) 210 zł C) 224 zł D) 336 zł
Medyczna maseczka ochronna wielokrotnego użytku z wymiennymi filtrami wskutek podwyżki zdrożała o 40% i kosztuje obecnie 106,40 zł. Cena maseczki przed podwyżką była równa
A) 63,84 zł B) 65,40 zł C) 76,00 zł D) 66,40 zł
Koszt uczestnictwa w obozie sportowym w 2018 r. wynosi 1620 zł. Wzrósł on w stosunku do kosztu z 2017 r. o 35%. Koszt uczestnictwa w obozie w 2017 r. wynosił
A) 1215 zł B) 1053 zł C) 1200 zł D) 567 zł
Cena książki wzrosła o 15% i wynosi 92 zł. Ile kosztowała książka przed podwyżką?
A) 105,8 zł B) 77 zł C) 78,2 zł D) 80 zł
Cena roweru po obniżce o 15% była równa 850 zł. Przed obniżką ten rower kosztował
A) 865,00 zł B) 850,15 zł C) 1000,00 zł D) 977,50 zł
W trójkącie równoramiennym podstawa 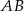 ma długość 8 cm. Promień okręgu, stycznego w punktach
ma długość 8 cm. Promień okręgu, stycznego w punktach 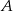 i
i 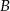 do prostych zawierających ramiona
do prostych zawierających ramiona 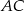 i
i 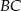 trójkąta, ma długość 5 cm. Oblicz pole trójkąta
trójkąta, ma długość 5 cm. Oblicz pole trójkąta 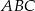 .
.
Ostrosłup ma 12 krawędzi. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 12 B) 9 C) 8 D) 7
Jeśli ostrosłup ma 50 krawędzi, to liczba jego ścian jest równa
A) 50 B) 26 C) 25 D) 22
Ostrosłup, który ma 12 krawędzi, ma
A) 6 ścian B) 7 ścian C) 8 ścian D) 9 ścian
Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa
A) 5 B) 7 C) 8 D) 10
O ile procent pole koła o promieniu długości 8 jest większe od pola koła wyznaczonego przez okrąg o równaniu 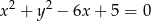 .
.
Dany jest trójkąt 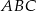 , w którym
, w którym 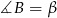 , a kąt zewnętrzny przy wierzchołku
, a kąt zewnętrzny przy wierzchołku 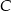 ma miarę
ma miarę  .
.
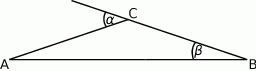
Wykaż, że jeśli 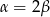 , to trójkąt
, to trójkąt 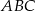 jest równoramienny.
jest równoramienny.
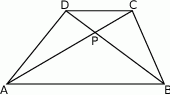
W trapezie 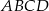 (
(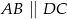 ) przekątne
) przekątne 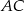 i
i 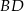 przecinają się w punkcie
przecinają się w punkcie 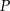 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 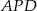 jest równe polu trójkąta
jest równe polu trójkąta 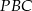 .
.
Dane są okręgi o równaniach 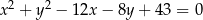 i
i 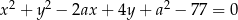 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
Dane są okręgi o równaniach 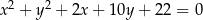 i
i 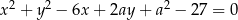 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
Rozwiąż nierówność 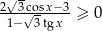 w przedziale
w przedziale 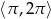 .
.
Środek 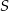 okręgu
okręgu 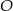 należy do prostej
należy do prostej 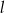 o równaniu
o równaniu 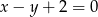 . Punkty
. Punkty 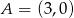 i
i 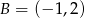 należą do tego okręgu.
należą do tego okręgu.
- Wyznacz równanie okręgu
 .
. - Wyznacz współrzędne takiego punktu
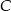 należącego do okręgu
należącego do okręgu 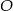 , że
, że 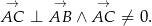
- Wyznacz równania stycznych
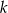 i
i 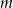 do okręgu
do okręgu 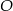 takich, że
takich, że 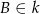 i
i 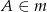 oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
Przekątne trapezu 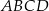 przecinają się w punkcie
przecinają się w punkcie 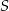 w ten sposób, że
w ten sposób, że 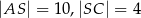 ,
, 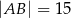 .
.
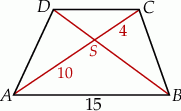
Długość odcinka 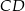 jest równa
jest równa
A) 4 B) 6 C) 8 D) 9

