Jaką wysokość ma romb, jeżeli wiadomo, że jego przekątne mają długości 12 i 16 centymetrów?
/Szkoła średnia
Jaką wysokość ma romb, jeżeli wiadomo, że jego przekątne mają długości 16 i 30?
Huta szkła produkuje kulki szklane o promieniu 5 cm. Do wysyłki będą one pakowane po 4 sztuki w sztywne pudełka w kształcie walca, którego wysokość wynosi 10 cm, a średnica 24 cm. Czy dobrze została dobrana średnica tych pudełek?
Liczba wszystkich sposobów utworzenia nieparzystych liczb trzycyfrowych o różnych cyfrach ze zbioru 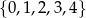 jest równa
jest równa
A) 18 B) 24 C) 36 D) 60
Liczba wszystkich sposobów utworzenia nieparzystych liczb trzycyfrowych o różnych cyfrach ze zbioru 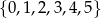 jest równa
jest równa
A) 18 B) 24 C) 48 D) 60
Wszystkich liczb naturalnych czterocyfrowych nieparzystych, w których występują wyłącznie cyfry 1, 2, 3, jest
A) 54 B) 81 C) 8 D) 27
Wszystkich liczb naturalnych czterocyfrowych parzystych, w których zapisie dziesiętnym występują tylko cyfry 2, 4, 7 (np.: 7272, 2222, 7244), jest
A) 16 B) 27 C) 54 D) 81
Wszystkich liczb naturalnych czterocyfrowych parzystych, w których występują wyłącznie cyfry 1, 2, 3, jest
A) 54 B) 81 C) 8 D) 27
Liczba wszystkich sposobów utworzenia nieparzystych liczb trzycyfrowych o cyfrach ze zbioru 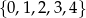 jest równa
jest równa
A) 18 B) 24 C) 20 D) 40
Na boku 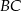 trójkąta równobocznego
trójkąta równobocznego 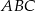 obrano taki punkt
obrano taki punkt 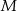 , że pole trójkąta
, że pole trójkąta 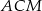 jest cztery razy mniejsze od pola trójkąta
jest cztery razy mniejsze od pola trójkąta 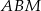 . Oblicz sinusy kątów
. Oblicz sinusy kątów 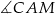 i
i 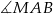 .
.
W trójkącie równoramiennym 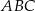 (
(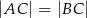 ) o kącie przy wierzchołku
) o kącie przy wierzchołku 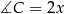 poprowadzono wysokość
poprowadzono wysokość 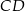 . Wiedząc, że
. Wiedząc, że 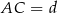 oblicz odległość środków okręgów wpisanych w trójkąty
oblicz odległość środków okręgów wpisanych w trójkąty 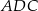 i
i 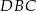 .
.
Dany jest ciąg o wyrazie ogólnym 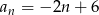 . Wybierz sto kolejnych początkowych wyrazów ciągu
. Wybierz sto kolejnych początkowych wyrazów ciągu 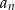 i oblicz dla jakiej liczby naturalnej
i oblicz dla jakiej liczby naturalnej 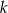 stosunek wyrazu stojącego na miejscu
stosunek wyrazu stojącego na miejscu 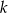 , licząc od początku, do wyrazu stojącego na miejscu
, licząc od początku, do wyrazu stojącego na miejscu 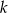 , licząc od końca, jest równy
, licząc od końca, jest równy 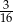 .
.
W ciągu arytmetycznym 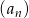 , określonym dla
, określonym dla 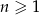 , spełniony jest warunek
, spełniony jest warunek 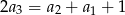 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 0 B) 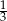 C)
C) 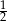 D) 1
D) 1
W ciągu arytmetycznym 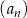 , określonym dla
, określonym dla 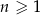 , spełniony jest warunek
, spełniony jest warunek 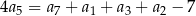 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 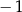 B)
B) 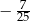 C)
C) 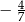 D) 2
D) 2
W ciągu arytmetycznym 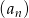 , określonym dla
, określonym dla 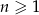 , spełniony jest warunek
, spełniony jest warunek 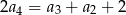 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 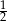 B) 1 C)
B) 1 C)  D) 0
D) 0
W ciągu arytmetycznym 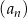 , określonym dla
, określonym dla 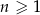 , spełniony jest warunek
, spełniony jest warunek 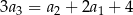 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 4 B) 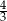 C) 2 D)
C) 2 D) 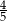
W ciągu arytmetycznym 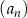 , określonym dla
, określonym dla 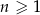 , spełniony jest warunek
, spełniony jest warunek 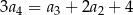 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 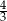 B) 1 C)
B) 1 C)  D)
D) 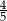
Kuba pożyczył od taty samochód, którym wyruszył z domu na spotkanie ze swoją dziewczyną. Przed wyjazdem obliczył, że jadąc ze średnią prędkością 60 km/h przybędzie na spotkanie dokładnie o umówionej godzinie. Po przejechaniu (z zaplanowaną prędkością) 60% drogi "złapał gumę", a zmiana koła zajęła mu 16 minut. Teraz, aby zdążyć na spotkanie, musiałby jechać z prędkością 120 km/h. Oblicz odległość od domu Kuby do miejsca spotkania z ukochaną.
Przedłużenia przeciwległych boków czworokąta wpisanego w okrąg tworzą kąty ostre o miarach 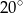 i
i 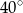 . Oblicz miary kątów czworokąta.
. Oblicz miary kątów czworokąta.
Odległość liczby  od liczby -8 na osi liczbowej jest równa
od liczby -8 na osi liczbowej jest równa
A) 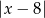 B)
B) 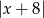 C)
C) 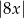 D)
D) 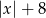
Odległość liczby  od liczby
od liczby 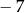 na osi liczbowej jest równa
na osi liczbowej jest równa
A) 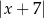 B)
B) 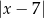 C)
C) 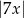 D)
D) 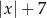
Odległość liczby  od liczby -6 na osi liczbowej jest równa
od liczby -6 na osi liczbowej jest równa
A) 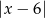 B)
B) 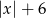 C)
C) 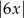 D)
D) 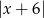
Zbadaj dla jakich wartości parametru 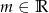 równanie
równanie 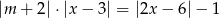 ma rozwiązanie.
ma rozwiązanie.
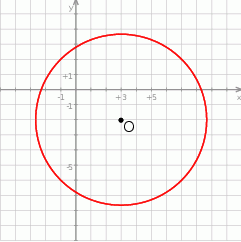
Punkt 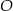 jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
A) 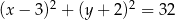 B)
B) 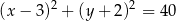
C) 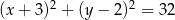 D)
D) 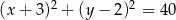
Wykaż, że dla dowolnej wartości parametru  równanie
równanie
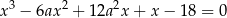
ma dokładnie jedno rozwiązanie rzeczywiste.
Połowa sumy 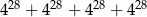 jest równa
jest równa
A) 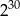 B)
B) 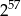 C)
C) 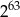 D)
D) 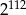
Wartość wyrażenia 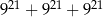 jest równa
jest równa
A) 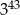 B)
B) 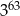 C)
C) 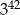 D)
D) 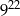
Trzecia część sumy 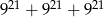 jest równa
jest równa
A) 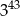 B)
B) 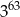 C)
C) 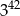 D)
D) 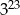
Wartość wyrażenia 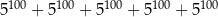 jest równa
jest równa
A) 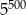 B)
B) 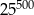 C)
C) 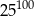 D)
D) 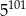
Liczba 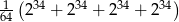 jest równa
jest równa
A) 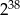 B)
B) 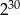 C)
C) 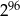 D)
D) 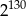
Wartość wyrażenia 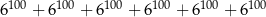 jest równa
jest równa
A) 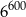 B)
B) 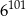 C)
C) 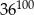 D)
D) 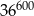
Prosta 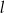 ma równanie
ma równanie 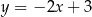 . Równaniem prostej prostopadłej do
. Równaniem prostej prostopadłej do 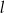 i przechodzącej przez punkt
i przechodzącej przez punkt 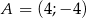 jest:
jest:
A) 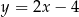 B)
B) 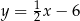 C)
C) 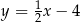 D)
D) 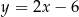
Prosta 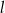 ma równanie
ma równanie 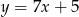 . Równanie prostej prostopadłej do
. Równanie prostej prostopadłej do 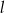 i przechodzącej przez punkt
i przechodzącej przez punkt 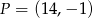 ma postać
ma postać
A) 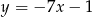 B)
B) 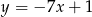 C)
C) 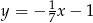 D)
D) 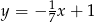
Punkt 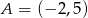 leży na prostej
leży na prostej 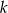 prostopadłej do prostej o równaniu
prostopadłej do prostej o równaniu 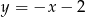 . Prosta
. Prosta 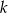 ma równanie
ma równanie
A) 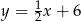 B)
B) 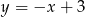 C)
C) 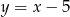 D)
D) 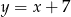
Prosta prostopadła do prostej o równaniu 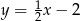 i przechodząca przez punkt
i przechodząca przez punkt 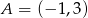 ma równanie
ma równanie
A) 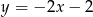 B)
B) 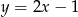 C)
C) 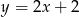 D)
D) 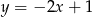
Na płaszczyźnie z układem współrzędnych proste 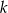 i
i 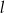 przecinają się pod kątem prostym w punkcie
przecinają się pod kątem prostym w punkcie 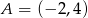 . Prosta
. Prosta 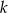 jest określona równaniem
jest określona równaniem 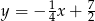 . Zatem prostą
. Zatem prostą 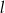 opisuje równanie
opisuje równanie
A) 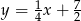 B)
B) 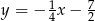 C)
C) 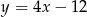 D)
D) 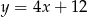
Dana jest prosta 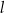 o równaniu
o równaniu 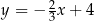 . Prosta
. Prosta 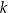 jest prostopadła do prostej
jest prostopadła do prostej 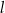 i przechodzi przez punkt
i przechodzi przez punkt 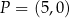 . Prosta
. Prosta 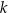 ma równanie
ma równanie
A) 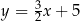 B)
B) 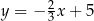 C)
C) 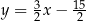 D)
D) 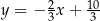
Prosta 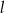 ma równanie
ma równanie 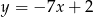 . Równanie prostej prostopadłej do
. Równanie prostej prostopadłej do 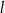 i przechodzącej przez punkt
i przechodzącej przez punkt 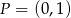 ma postać
ma postać
A) 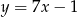 B)
B) 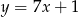 C)
C) 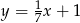 D)
D) 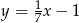
Równanie prostej prostopadłej do prostej 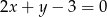 i przechodzącej przez punkt
i przechodzącej przez punkt 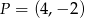 ma postać
ma postać
A) 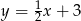 B)
B) 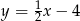 C)
C) 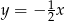 D)
D) 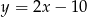
Punkt 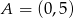 leży na prostej
leży na prostej 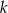 prostopadłej do prostej o równaniu
prostopadłej do prostej o równaniu 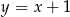 . Prosta
. Prosta 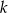 ma równanie
ma równanie
A) 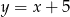 B)
B) 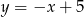 C)
C) 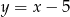 D)
D) 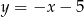
Prosta o równaniu 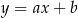 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 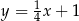 i przechodzi przez punkt
i przechodzi przez punkt 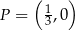 , gdy
, gdy
A) 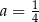 i
i 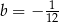 B)
B) 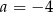 i
i 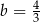
C) 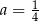 i
i 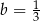 D)
D) 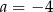 i
i 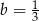
Na płaszczyźnie z układem współrzędnych proste 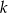 i
i 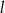 przecinają się pod kątem prostym w punkcie
przecinają się pod kątem prostym w punkcie 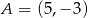 . Prosta
. Prosta 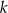 jest określona równaniem
jest określona równaniem 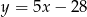 . Zatem prostą
. Zatem prostą 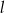 opisuje równanie
opisuje równanie
A) 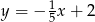 B)
B) 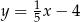 C)
C) 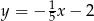 D)
D) 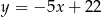
Prostą prostopadłą do prostej 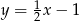 i przechodzącą przez punkt
i przechodzącą przez punkt 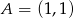 opisuje równanie:
opisuje równanie:
A) 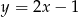 B)
B) 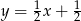 C)
C) 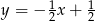 D)
D) 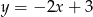
Prosta 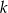 ma równanie
ma równanie 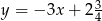 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 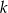 , przechodzącej przez punkt
, przechodzącej przez punkt 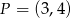 .
.
A) 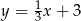 B)
B) 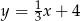 C)
C) 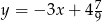 D)
D) 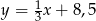
Prosta o równaniu 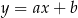 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 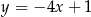 i przechodzi przez punkt
i przechodzi przez punkt 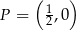 , gdy
, gdy
A) 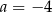 i
i 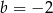 B)
B) 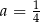 i
i 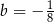
C) 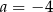 i
i 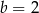 D)
D) 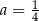 i
i 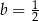
Dana jest prosta 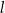 o równaniu
o równaniu 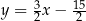 . Prosta
. Prosta 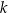 jest prostopadła do prostej
jest prostopadła do prostej 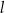 i przechodzi przez punkt
i przechodzi przez punkt 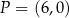 . Prosta
. Prosta 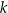 ma równanie
ma równanie
A) 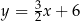 B)
B) 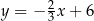 C)
C) 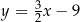 D)
D) 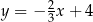
Dana jest prosta 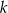 o równaniu
o równaniu 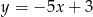 . Równanie prostej prostopadłej do prostej
. Równanie prostej prostopadłej do prostej 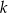 i przechodzącej przez punkt
i przechodzącej przez punkt 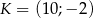 ma postać
ma postać
A) 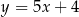 B)
B) 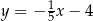 C)
C) 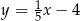 D)
D) 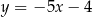
Klasa IIIb liczy o jednego ucznia więcej niż klasa IIIa. Na koniec roku okazało się, że suma ocen z matematyki uzyskanych przez uczniów klasy IIIa jest równa 97,5 i jest jednocześnie równa sumie ocen z matematyki uzyskanych przez uczniów klasy IIIb. Gdy obliczono średnie z tych ocen w każdej z klas to okazało się, że średnia w klasie IIIa była wyższa o 0,15 niż średnia uzyskana w klasie IIIb. Oblicz ilu uczniów liczą obie klasy.
Na okręgu o środku w punkcie 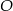 leżą punkty
leżą punkty 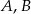 i
i 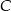 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 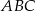 ma miarę
ma miarę 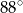 , a kąt
, a kąt 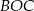 ma miarę o
ma miarę o 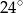 mniejszą od miary kąta
mniejszą od miary kąta 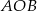 .
.
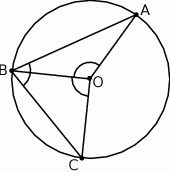
Kąt 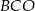 ma miarę
ma miarę
A) 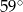 B)
B) 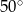 C)
C) 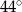 D)
D) 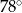
Czy kwadratowe lustro o boku długości 2,2 m można przenieść przez drzwi o szerokości 1 m i wysokości 2 m?
Rozwiąż równanie 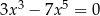 .
.
W trójkącie 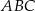 dane są wierzchołki
dane są wierzchołki 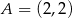 ,
, 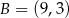 ,
, 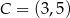 . Trójkąt
. Trójkąt 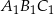 jest obrazem trójkąta
jest obrazem trójkąta 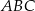 w jednokładności o środku
w jednokładności o środku 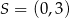 i skali
i skali 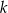 . Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie
. Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie 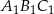 ma długość
ma długość 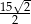 . Skala jednokładności
. Skala jednokładności 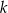 wynosi
wynosi
A) 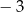 B)
B) 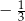 C)
C) 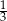 D) 3
D) 3

