Dany jest trójkąt prostokątny 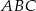 , w którym
, w którym 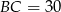 ,
, 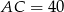 i
i 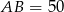 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 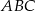 jest styczny do boku
jest styczny do boku 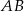 w punkcie
w punkcie 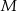 . Oblicz długość odcinka
. Oblicz długość odcinka 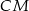 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
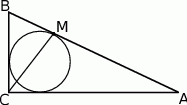
Dany jest trójkąt prostokątny 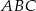 , w którym
, w którym 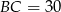 ,
, 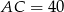 i
i 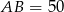 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 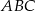 jest styczny do boku
jest styczny do boku 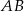 w punkcie
w punkcie 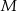 . Oblicz długość odcinka
. Oblicz długość odcinka 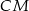 .
.

W trójkąt prostokątny o przyprostokątnych długości 15 i 20 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek kąta prostego tego trójkąta z punktem wspólnym okręgu i przeciwprostokątnej.
Proste 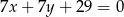 i
i 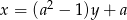 przecinają się pod kątem
przecinają się pod kątem 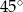 . Wyznacz liczbę
. Wyznacz liczbę  .
.
Dany jest trójkąt prostokątny o polu 6, w którym długość przeciwprostokątnej jest liczbą z przedziału 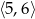 . Wykaż, że suma długości przyprostokątnych tego trójkąta jest liczbą z przedziału
. Wykaż, że suma długości przyprostokątnych tego trójkąta jest liczbą z przedziału 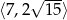 .
.
W trójkąt równoramienny 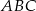 (
(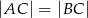 ) o długości podstawy
) o długości podstawy 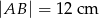 wpisano kwadrat o boku długości 5 cm. Oblicz pole trójkąta
wpisano kwadrat o boku długości 5 cm. Oblicz pole trójkąta 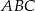 .
.
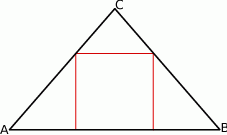
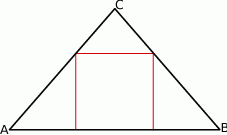
W trójkąt równoramienny 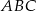 (
(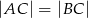 ) o długości podstawy
) o długości podstawy 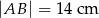 wpisano kwadrat o boku długości 6 cm. Oblicz pole trójkąta
wpisano kwadrat o boku długości 6 cm. Oblicz pole trójkąta 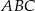 .
.
Liczbą odwrotną do liczby 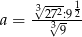 jest
jest
A) 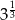 B)
B) 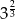 C)
C) 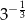 D)
D) 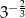
Liczbą odwrotną do liczby 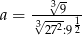 jest
jest
A) 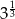 B)
B) 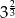 C)
C) 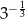 D)
D) 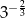
Wyznacz wzór funkcji liniowej 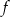 , która dla każdego
, która dla każdego 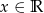 spełnia warunek
spełnia warunek 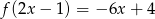 .
.
Suma długości wszystkich krawędzi ostrosłupa prawidłowego trójkątnego jest równa 96, a krawędź boczna tworzy z płaszczyzną podstawy kąt, którego cosinus jest równy 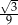 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Na okręgu o równaniu 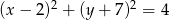 leży punkt
leży punkt
A) 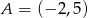 B)
B) 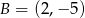 C)
C) 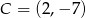 D)
D) 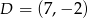
Do okręgu o równaniu 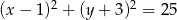 należy punkt
należy punkt
A) 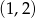 B)
B) 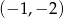 C)
C) 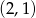 D)
D) 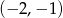
Na okręgu o równaniu 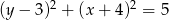 leży punkt
leży punkt
A) 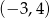 B)
B) 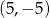 C)
C) 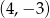 D)
D) 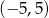
Pięć identycznych metalowych stożków o promieniu podstawy  przetopiono na jeden walec, którego wysokość jest równa
przetopiono na jeden walec, którego wysokość jest równa 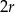 i jest dwa razy krótsza od jego promienia podstawy. Gdyby te same stożki przetopiono na kule o promieniu
i jest dwa razy krótsza od jego promienia podstawy. Gdyby te same stożki przetopiono na kule o promieniu  , to ile takich kul by otrzymano?
, to ile takich kul by otrzymano?
A) 32 B) 16 C) 8 D) 24
Naszkicuj wykresy funkcji 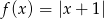 oraz
oraz 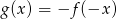 . Podaj wzór funkcji
. Podaj wzór funkcji 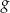 .
.
Naszkicuj wykresy funkcji 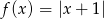 oraz
oraz 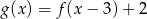 . Podaj wzór funkcji
. Podaj wzór funkcji 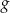 .
.
Naszkicuj wykresy funkcji 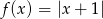 oraz
oraz 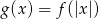 . Podaj wzór funkcji
. Podaj wzór funkcji 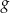 .
.
Oblicz, ile jest liczb naturalnych czterocyfrowych, w których zapisie pierwsza cyfra jest parzysta, a pozostałe nieparzyste.
Oblicz, ile jest liczb naturalnych czterocyfrowych, w których zapisie pierwsza cyfra jest liczbą podzielną przez 3, a pozostałe są parzyste.
Cztery liczby tworzą ciąg geometryczny. Wyznacz te liczby wiedząc, że suma pierwszej i czwartej wynosi 36, a suma drugiej i trzeciej liczby wynosi 24.
Wysokość 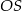 walca jest równa 2, a cosinus kąta
walca jest równa 2, a cosinus kąta 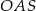 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy  .
.
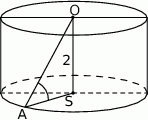
Pole powierzchni bocznej tego walca jest równe
A) 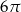 B)
B) 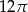 C)
C) 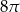 D)
D) 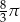
Jeżeli  oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
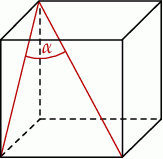
A) 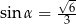 B)
B) 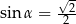 C)
C) 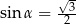 D)
D) 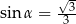
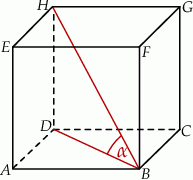
Dany jest sześcian 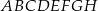 . Sinus kąta
. Sinus kąta  nachylenia przekątnej
nachylenia przekątnej 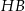 tego sześcianu do płaszczyzny podstawy
tego sześcianu do płaszczyzny podstawy 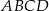 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 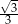 B)
B) 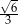 C)
C) 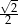 D)
D) 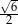
Jeżeli  oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
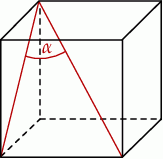
A) 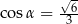 B)
B) 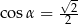 C)
C) 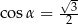 D)
D) 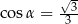
Jeżeli  oznacza miarę kąta między przekątnymi ścian sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątnymi ścian sześcianu (zobacz rysunek), to
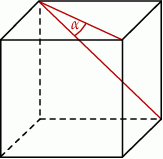
A) 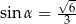 B)
B) 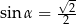 C)
C) 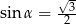 D)
D) 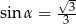
Pierwiastkami wielomianu stopnia trzeciego 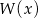 są liczby
są liczby 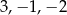 , a współczynnik stojący przy najwyższej potędze zmiennej
, a współczynnik stojący przy najwyższej potędze zmiennej  jest równy 3. Wielomian ten można zapisać w postaci
jest równy 3. Wielomian ten można zapisać w postaci
A) 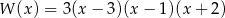 B)
B) 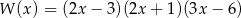
C) 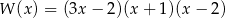 D)
D) 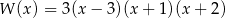
Pierwiastkami wielomianu stopnia trzeciego 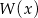 są liczby 2,-1,-3, a współczynnik stojący przy najwyższej potędze zmiennej
są liczby 2,-1,-3, a współczynnik stojący przy najwyższej potędze zmiennej  jest równy 4. Wielomian ten można zapisać w postaci
jest równy 4. Wielomian ten można zapisać w postaci
A) 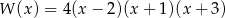 B)
B) 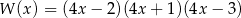
C) 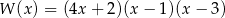 D)
D) 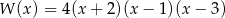
Pierwiastkami wielomianu stopnia trzeciego 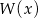 są liczby -3,5,-1, a współczynnik stojący przy najwyższej potędze zmiennej
są liczby -3,5,-1, a współczynnik stojący przy najwyższej potędze zmiennej  jest równy 2. Wielomian ten można zapisać w postaci
jest równy 2. Wielomian ten można zapisać w postaci
A) 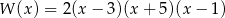 B)
B) 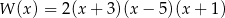
C) 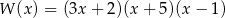 D)
D) 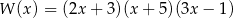
Wykaż, że jeżeli 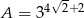 i
i 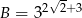 , to
, to 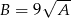 .
.
Wykaż, że jeżeli 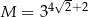 i
i 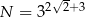 , to
, to 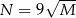 .
.
Zbiór punktów wspólnych kuli i prostej może być
A) zbiorem dwuelementowym B) zbiorem jednoelementowym C) okręgiem D) kołem
Zbiór punktów wspólnych kuli i płaszczyzny może być
A) zbiorem dwuelementowym B) okręgiem C) zbiorem jednoelementowym D) sferą
W trapezie równoramiennym jedna z podstaw jest dwa razy dłuższa od drugiej, a przekątna trapezu dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego pole jest równe 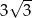 .
.
W trapezie równoramiennym stosunek długości podstaw jest równy 3:4, a przekątna trapezu dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego pole jest równe 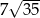 .
.
Skala Richtera służy do określania siły trzęsień ziemi. Siła ta opisana jest wzorem 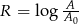 , gdzie
, gdzie 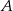 oznacza amplitudę trzęsienia wyrażoną w centymetrach,
oznacza amplitudę trzęsienia wyrażoną w centymetrach, 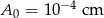 jest stałą, nazywaną amplitudą wzorcową. 5 maja 2014 roku w Tajlandii miało miejsce trzęsienie ziemi o sile 6,2 w skali Richtera. Oblicz amplitudę trzęsienia ziemi w Tajlandii i rozstrzygnij, czy jest ona większa, czy – mniejsza od 100 cm.
jest stałą, nazywaną amplitudą wzorcową. 5 maja 2014 roku w Tajlandii miało miejsce trzęsienie ziemi o sile 6,2 w skali Richtera. Oblicz amplitudę trzęsienia ziemi w Tajlandii i rozstrzygnij, czy jest ona większa, czy – mniejsza od 100 cm.
Skala Richtera służy do określania siły trzęsień ziemi. Siła ta opisana jest wzorem 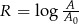 , gdzie
, gdzie 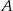 oznacza amplitudę trzęsienia wyrażoną w centymetrach,
oznacza amplitudę trzęsienia wyrażoną w centymetrach, 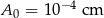 jest stałą, nazywaną amplitudą wzorcową. 27 lutego 2010 roku w Chile miało miejsce trzęsienie ziemi o sile 8,8 w skali Richtera. Oblicz amplitudę trzęsienia ziemi w Chile i rozstrzygnij, czy jest ona większa, czy – mniejsza od 100 m.
jest stałą, nazywaną amplitudą wzorcową. 27 lutego 2010 roku w Chile miało miejsce trzęsienie ziemi o sile 8,8 w skali Richtera. Oblicz amplitudę trzęsienia ziemi w Chile i rozstrzygnij, czy jest ona większa, czy – mniejsza od 100 m.
W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej prostopadła do krawędzi podstawy ostrosłupa jest równa 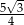 , a pole powierzchni bocznej tego ostrosłupa jest równe
, a pole powierzchni bocznej tego ostrosłupa jest równe 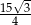 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
