Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4. Jakie pole ma koło opisane na tym kwadracie?
/Szkoła średnia
Średnia wieku w pewnej grupie studentów jest równa 23 lata. Średnia wieku tych studentów i ich opiekuna jest równa 24 lata. Opiekun ma 39 lat. Oblicz, ilu studentów jest w tej grupie.
Średnia wieku w pewnej grupie uczniów jest równa 14 lat. Średnia wieku tych uczniów i ich opiekuna jest równa 16 lat. Opiekun ma 40 lat. Oblicz, ilu uczniów jest w tej grupie.
Ile jest liczb naturalnych trzycyfrowych, których kolejne cyfry tworzą ciąg geometryczny o ilorazie równym 2 lub 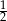 ?
?
A) 4 B) 16 C) 8 D) 9
Ile jest liczb naturalnych czterocyfrowych, których kolejne cyfry tworzą ciąg arytmetyczny o różnicy 2 lub 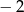 ?
?
A) 7 B) 6 C) 12 D) 9
Bok rombu ma taką samą długość jak przekątna kwadratu. Pole rombu jest równe polu kwadratu. Zatem kąt ostry tego rombu ma miarę
A) 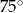 B)
B) 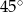 C)
C) 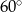 D)
D) 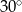
Bok 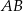 czworokąta
czworokąta 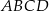 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 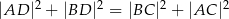 .
.
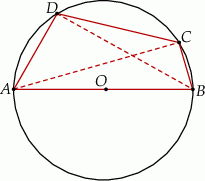
Przekątna 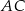 czworokąta
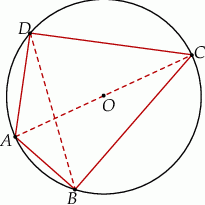
czworokąta 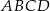 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że  .
.
Wielomian 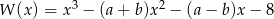 jest podzielny przez dwumian
jest podzielny przez dwumian 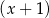 , a reszta z dzielenia wielomianu
, a reszta z dzielenia wielomianu 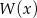 przez dwumian
przez dwumian 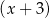 wynosi
wynosi 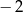 . Oblicz
. Oblicz  i
i 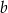 , a następnie rozwiąż nierówność
, a następnie rozwiąż nierówność 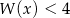 .
.
Wykaż, że dla dowolnej liczby 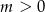 prawdziwa jest nierówność
prawdziwa jest nierówność 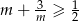 .
.
Wykaż, że dla dowolnej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność 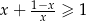 .
.
Udowodnij, że dla dowolnej dodatniej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
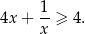
Udowodnij, że dla dowolnej ujemnej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
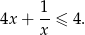
Wykaż, że dla dowolnej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność 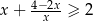 .
.
Za 4 lata Ula będzie miała dwa razy więcej lat niż miała 2 lata temu. Ile lat ma Ula?
Nierówność 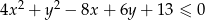 przedstawia na płaszczyźnie
przedstawia na płaszczyźnie
A) okrąg B) koło C) punkt D) zbiór pusty
Nierówność 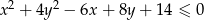 przedstawia na płaszczyźnie
przedstawia na płaszczyźnie
A) okrąg B) koło C) punkt D) zbiór pusty
Nierówność 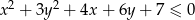 przedstawia na płaszczyźnie
przedstawia na płaszczyźnie
A) punkt B) koło C) okrąg D) zbiór pusty
W pudełku jest 8 kul, z czego 5 białych i 3 czarne. Do tego pudełka dołożono  kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe
kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe 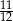 . Oblicz
. Oblicz  .
.
W pudełku jest 9 kul, z czego 7 białych i 2 czarne. Do tego pudełka dołożono  kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe
kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe 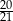 . Oblicz
. Oblicz  .
.
W urnie jest 7 kul czarnych i 5 białych. Sześć z nich przekładamy do drugiej urny, początkowo pustej, i z niej losujemy 2 kule bez zwracania. Jakie jest prawdopodobieństwo, że druga z nich będzie biała.
Rysunek przedstawia wykres funkcji 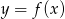 .
.
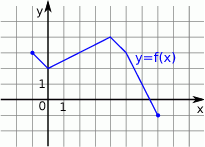
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 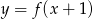 .
.
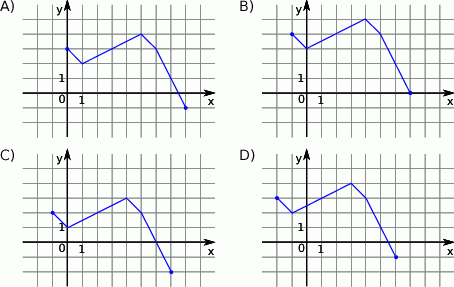
Na rysunku dany jest wykres funkcji 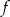 .
.
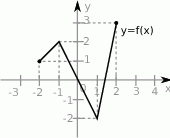
Wykres funkcji 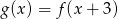 jest przedstawiony na rysunku:
jest przedstawiony na rysunku:
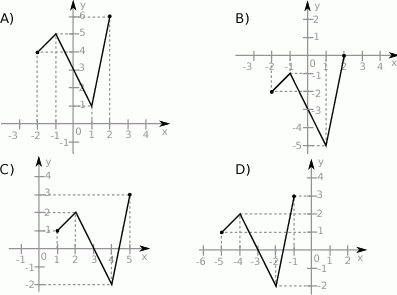
Poniżej przedstawiony jest wykres funkcji 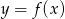 .
.
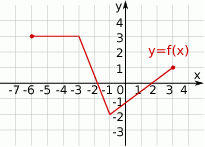
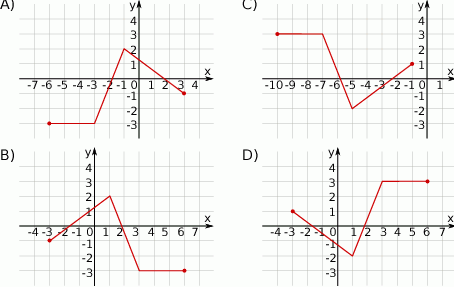
Wskaż wykres funkcji 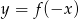 .
.
Rysunek przedstawia wykres funkcji 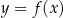 .
.
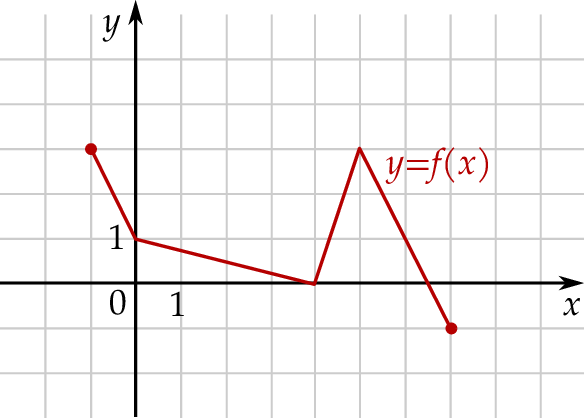
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 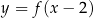 .
.
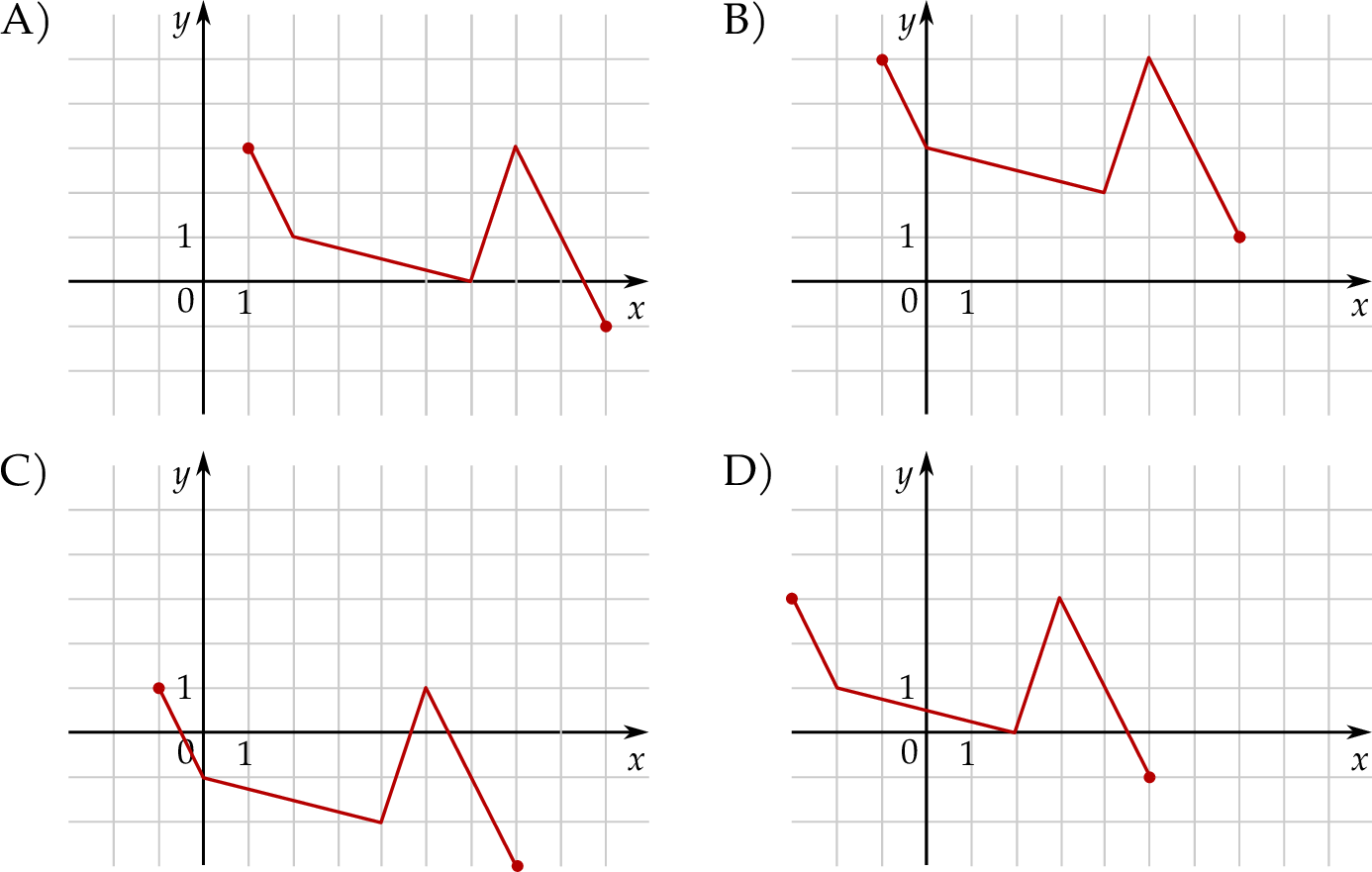
Rysunek przedstawia wykres funkcji 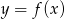 .
.
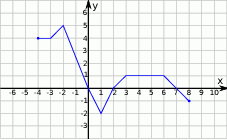
Wskaż wykres funkcji 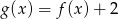 .
.
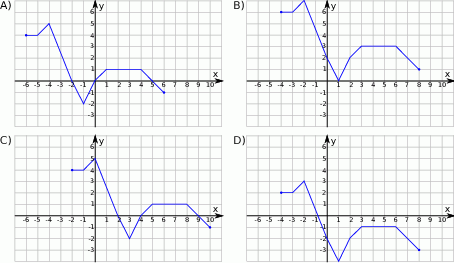
Rysunek przedstawia wykres funkcji 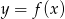 .
.
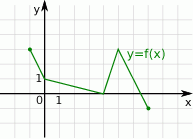
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 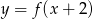 .
.
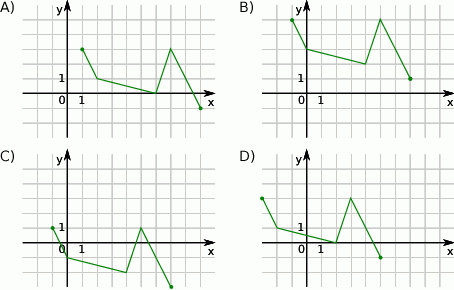
Rysunek przedstawia wykres funkcji 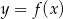 .
.
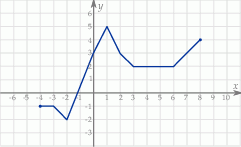
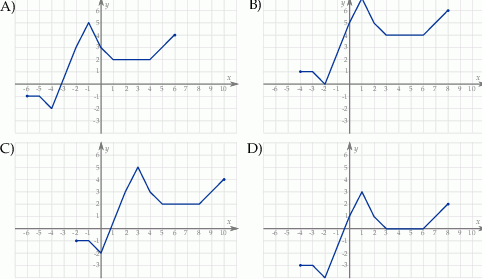
Wskaż wykres funkcji 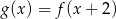 .
.
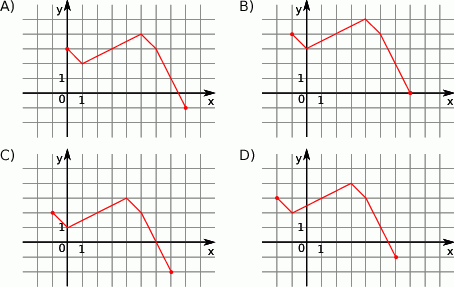
Rysunek przedstawia wykres funkcji 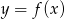 .
.
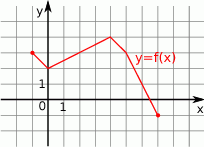
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 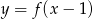 .
.
Rysunek przedstawia wykres funkcji 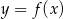 .
.
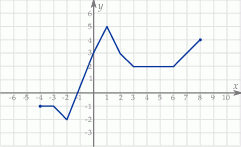
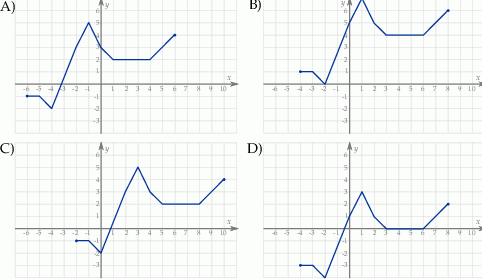
Wskaż wykres funkcji 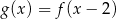 .
.
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
A) 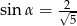 B)
B) 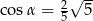 C)
C) 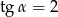 D)
D) 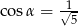
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Natomiast przeciwprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Natomiast przeciwprostokątna ma długość 6 cm. Zatem
A) 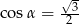 B)
B) 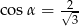 C)
C) 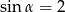 D)
D) 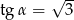
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
A) 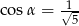 B)
B) 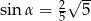 C)
C) 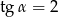 D)
D) 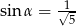
Oblicz dla jakich wartości parametrów 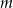 i
i  proste o równaniach:
proste o równaniach: 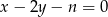 i
i 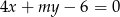 są dwiema różnymi prostymi równoległymi.
są dwiema różnymi prostymi równoległymi.
Wykaż, że równanie 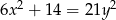 nie ma rozwiązań całkowitych.
nie ma rozwiązań całkowitych.
Posługując się wykresem funkcji 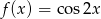 dla
dla 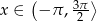 , rozwiąż nierówność
, rozwiąż nierówność 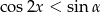 wiedząc, że miara kąta
wiedząc, że miara kąta  jest równa mierze łukowej kąta środkowego okręgu opartego na
jest równa mierze łukowej kąta środkowego okręgu opartego na 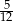 okręgu.
okręgu.
W malejącym ciągu geometrycznym 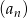 mamy
mamy 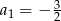 i
i 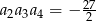 . Iloraz tego ciągu równy
. Iloraz tego ciągu równy
A) 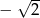 B)
B) 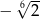 C)
C) 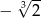 D)
D) 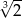
Dany jest ciąg 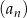 określony wzorem
określony wzorem 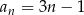 dla każdej liczby naturalnej
dla każdej liczby naturalnej 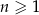 . Najmniejszą wartością
. Najmniejszą wartością  , dla której wyraz
, dla której wyraz 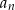 jest większy od 25, jest
jest większy od 25, jest
A) 8 B) 9 C) 7 D) 26
Dany jest ciąg 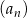 określony wzorem
określony wzorem 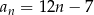 dla każdej liczby naturalnej
dla każdej liczby naturalnej 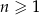 . Najmniejszą wartością
. Najmniejszą wartością  , dla której wyraz
, dla której wyraz 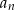 jest większy od 2023, jest
jest większy od 2023, jest
A) 170 B) 169 C) 168 D) 203
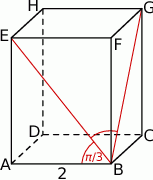
Przekątna 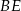 ściany bocznej prostopadłościanu
ściany bocznej prostopadłościanu 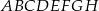 tworzy z krawędzią podstawy
tworzy z krawędzią podstawy 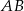 kąt o mierze
kąt o mierze 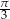 . Przekątne
. Przekątne 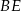 i
i 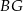 ścian bocznych tworzą kąt, którego cosinus jest równy
ścian bocznych tworzą kąt, którego cosinus jest równy 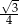 , a krawędź
, a krawędź 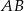 podstawy ma długość 2. Oblicz promień okręgu opisanego na trójkącie
podstawy ma długość 2. Oblicz promień okręgu opisanego na trójkącie 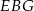 .
.
Dana jest funkcja 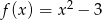 . Znajdź miejsca zerowe funkcji
. Znajdź miejsca zerowe funkcji ![g(x ) = [f(x)]](https://img.zadania.info/zad/9606251/HzadT1x.gif) , gdzie
, gdzie ![[a]](https://img.zadania.info/zad/9606251/HzadT2x.gif) oznacza największą liczbę całkowitą nie większą od
oznacza największą liczbę całkowitą nie większą od  .
.

