Ile punktów wspólnych ma prosta 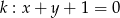 z okręgiem
z okręgiem 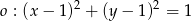 ?
?
A) 3 B) 2 C) 1 D) 0
/Szkoła średnia
Ile punktów wspólnych ma prosta 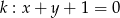 z okręgiem
z okręgiem 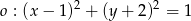 ?
?
A) 3 B) 2 C) 1 D) 0
Ile punktów wspólnych ma prosta 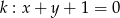 z okręgiem
z okręgiem 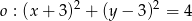 ?
?
A) 0 B) 1 C) 2 D) 3
Przez pewien okres czasu prowadzono regularne pomiary temperatury w miejscowości Jelenia Góra. Wyniki pomiarów zapisano w tabeli
Temperatura w 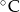 | -1 | 2 | 3 |
| Liczba wskazań | 5 | m | 2 |
Obliczono, że średnia temperatura wynosi 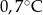 . Zatem liczba
. Zatem liczba 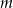 jest równa
jest równa
A) 13 B) 4 C) 10 D) 3
Przez pewien okres czasu prowadzono regularne pomiary temperatury w miejscowości Kłodzko. Wyniki pomiarów zapisano w tabeli
Temperatura w 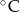 | 1 | 2 | 3 |
| Liczba wskazań | 6 | m | 2 |
Obliczono, że średnia temperatura wynosi 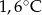 . Zatem liczba
. Zatem liczba 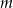 jest równa
jest równa
A) 5 B) 4 C) 2 D) 3
Przez pewien okres czasu prowadzono regularne pomiary temperatury w miejscowości Rabka. Wyniki pomiarów zapisano w tabeli
Temperatura w 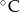 | -3 | -2 | -1 |
| Liczba wskazań | 3 | m | 4 |
Obliczono, że średnia temperatura wynosi 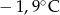 . Zatem liczba
. Zatem liczba 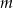 jest równa
jest równa
A) 3 B) 4 C) 13 D) 5
Dana jest funkcja 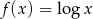 .
.
- Naszkicuj wykres funkcji
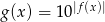 .
. - Udowodnij, że jeżeli
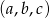 jest ciągiem geometrycznym o wyrazach dodatnich to
jest ciągiem geometrycznym o wyrazach dodatnich to 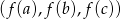 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Pusta bańka na mleko o pojemności 10 litrów ma masę 6,5 kg. Jeden litr mleka ma masę 1,03 kg. Niech  oznacza liczbę litrów mleka w tej bańce, a
oznacza liczbę litrów mleka w tej bańce, a 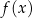 oznacza wyrażoną w kilogramach masę bańki wraz z mlekiem, gdzie
oznacza wyrażoną w kilogramach masę bańki wraz z mlekiem, gdzie ![x ∈ [0,1 0]](https://img.zadania.info/zad/9628036/HzadT2x.png) . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 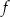 jest malejąca. jest malejąca. | P | F |
Funkcja 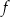 nie ma miejsc zerowych. nie ma miejsc zerowych. | P | F |
Pole podstawy stożka jest trzy razy mniejsze od jego pola powierzchni bocznej. Wówczas kąt  rozwarcia stożka spełnia warunek
rozwarcia stożka spełnia warunek
A) 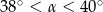 B)
B) 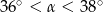 C)
C) 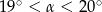 D)
D) 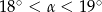
Funkcja 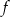 jest określona wzorem
jest określona wzorem 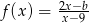 dla
dla 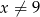 . Ponadto wiemy, że
. Ponadto wiemy, że 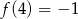 . Oblicz współczynnik
. Oblicz współczynnik 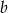 .
.
Dane są dwa pojemniki. W pierwszym z nich znajduje się 9 kul: 4 białe, 3 czarne i 2 zielone. W drugim pojemniku jest 6 kul: 2 białe, 3 czarne i 1 zielona. Z każdego pojemnika losujemy po jednej kuli. Oblicz prawdopodobieństwo wylosowania dwóch kul tego samego koloru.
Dane są dwa pojemniki. W pierwszym z nich znajduje się 9 kul: 2 białe, 5 czarnych i 2 zielone. W drugim pojemniku jest 6 kul: 3 białe, 1 czarna i 2 zielone. Z każdego pojemnika losujemy po jednej kuli. Oblicz prawdopodobieństwo wylosowania dwóch kul tego samego koloru.
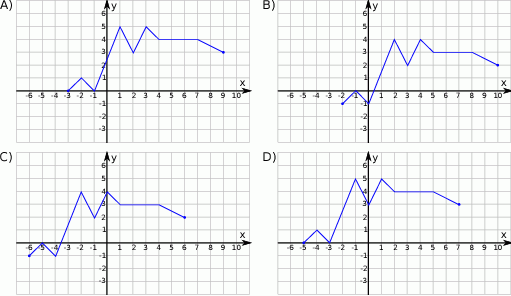
Rysunek przedstawia wykres funkcji 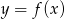 .
.
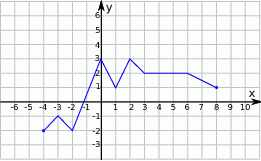
Wskaż wykres funkcji 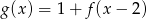 .
.
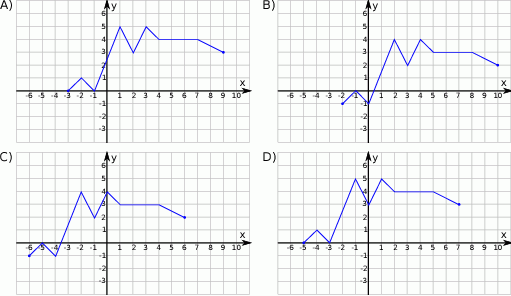
Na rysunku przedstawiony jest wykres funkcji 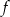 .
.
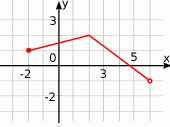
Wykres funkcji 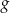 , określonej wzorem
, określonej wzorem 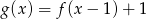 , przedstawia rysunek:
, przedstawia rysunek:
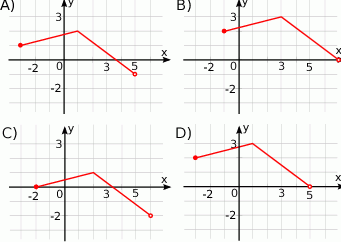
Na rysunku przedstawiony jest wykres funkcji 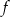 .
.
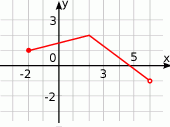
Wykres funkcji 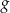 , określonej wzorem
, określonej wzorem 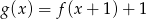 , przedstawia rysunek:
, przedstawia rysunek:
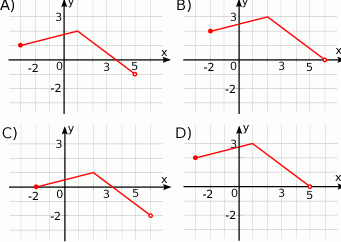
Rysunek przedstawia wykres funkcji 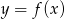 .
.
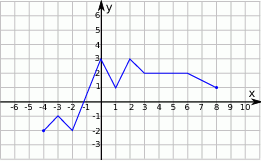
Wskaż wykres funkcji 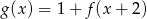 .
.
Udowodnij, że 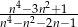 , dla
, dla 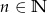 i
i 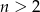 jest ułamkiem właściwym.
jest ułamkiem właściwym.
Niech 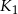 będzie kwadratem o boku długości
będzie kwadratem o boku długości  . Konstruujemy kolejno kwadraty
. Konstruujemy kolejno kwadraty 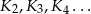 takie, że bok kolejnego kwadratu jest równy przekątnej poprzedniego kwadratu. Oblicz sumę pól kwadratów
takie, że bok kolejnego kwadratu jest równy przekątnej poprzedniego kwadratu. Oblicz sumę pól kwadratów 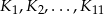 .
.
Narysuj dowolny trójkąt 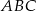 a następnie skonstruuj trójkąt
a następnie skonstruuj trójkąt 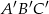 podobny do trójkąta
podobny do trójkąta 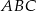 w skali podobieństwa
w skali podobieństwa 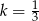 .
.
Wyznacz wszystkie wartości parametru 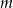 , dla których dziedziną funkcji
, dla których dziedziną funkcji
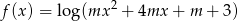
jest zbiór wszystkich liczb rzeczywistych.
W rombie jedna z przekątnych jest dłuższa od drugiej o 3 cm. Dla jakich długości przekątnych pole rombu jest większe od 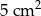 ?
?
Pierwsza współrzędna wierzchołka paraboli o równaniu 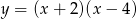 jest równa
jest równa
A) 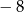 B)
B) 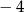 C) 1 D) 2
C) 1 D) 2
Funkcja kwadratowa 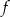 jest określona wzorem
jest określona wzorem 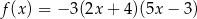 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 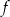 , ma współrzędną
, ma współrzędną  równą
równą
A) 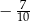 B)
B) 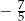 C)
C) 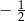 D)
D) 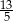
Funkcja kwadratowa 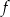 jest określona wzorem
jest określona wzorem 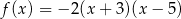 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 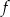 , ma współrzędną
, ma współrzędną  równą
równą
A) 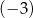 B)
B) 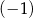 C) 1 D) 5
C) 1 D) 5
Pierwsza współrzędna wierzchołka paraboli o równaniu 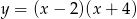 jest równa
jest równa
A) 8 B) 4 C) 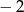 D)
D) 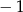
Wyznacz wszystkie wartości  , dla których nierówność
, dla których nierówność 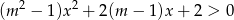 jest prawdziwa dla każdego
jest prawdziwa dla każdego 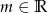 .
.
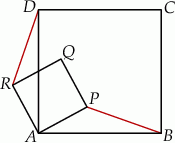
Czworokąty 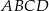 i
i 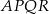 są kwadratami. Udowodnij, że
są kwadratami. Udowodnij, że 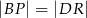 .
.
Trzywyrazowy ciąg geometryczny jest rosnący. Iloczyn wszystkich wyrazów tego ciągu jest równy -8, a iloraz pierwszego wyrazu przez trzeci wynosi 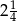 . Wyznacz ten ciąg.
. Wyznacz ten ciąg.
Liczba 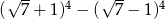 jest równa
jest równa
A) 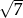 B)
B) 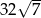 C)
C) 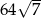 D) 2
D) 2
Liczba 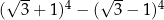 jest równa
jest równa
A) 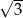 B)
B) 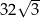 C)
C) 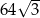 D) 2
D) 2
Zbadaj liczbę rozwiązań równania ze względu na wartość parametru 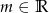 . Napisz wzór i narysuj wykres funkcji
. Napisz wzór i narysuj wykres funkcji 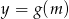 , która każdej wartości parametru
, która każdej wartości parametru 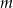 przyporządkowuje liczbę rozwiązań równania
przyporządkowuje liczbę rozwiązań równania 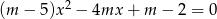 .
.
Punkt 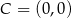 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 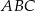 , którego wierzchołek
, którego wierzchołek 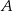 leży na osi
leży na osi 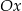 , a wierzchołek
, a wierzchołek 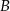 na osi
na osi 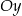 układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka
układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka 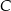 przecina przeciwprostokątną
przecina przeciwprostokątną 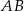 w punkcie
w punkcie 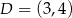 .
.
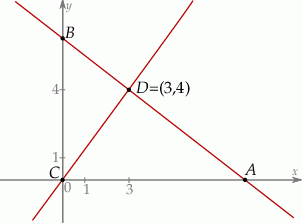
Oblicz współrzędne wierzchołków 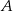 i
i 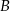 tego trójkąta oraz długość przeciwprostokątnej
tego trójkąta oraz długość przeciwprostokątnej 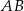 .
.
Punkt 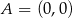 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 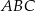 , którego wierzchołek
, którego wierzchołek 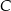 leży na osi
leży na osi 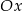 , a wierzchołek
, a wierzchołek 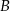 na osi
na osi 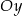 układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka
układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka 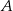 przecina przeciwprostokątną
przecina przeciwprostokątną 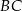 w punkcie
w punkcie 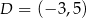 .
.
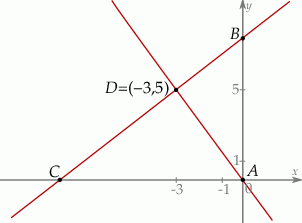
Oblicz współrzędne wierzchołków 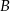 i
i 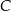 tego trójkąta oraz długość przeciwprostokątnej
tego trójkąta oraz długość przeciwprostokątnej  .
.

