Ostrosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź podstawy długości  i środek wysokości ostrosłupa. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem
i środek wysokości ostrosłupa. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość i pole powierzchni bocznej ostrosłupa.
. Oblicz objętość i pole powierzchni bocznej ostrosłupa.
/Szkoła średnia
Funkcja 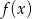 , gdzie
, gdzie 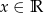 dana jest wzorem
dana jest wzorem
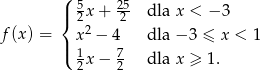
- Narysuj wykres funkcji
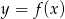 .
. - Odczytaj z wykresu rozwiązanie nierówności
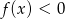 .
.
Czterdzieści osób usadzono w sposób losowy przy czterech dziesięcioosobowych okrągłych stołach. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że trzy ustalone wcześniej osoby siedzą na trzech sąsiednich miejscach.
Czterdzieści osób usadzono w sposób losowy przy czterech dziesięcioosobowych okrągłych stołach. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że trzy ustalone wcześniej osoby siedzą przy jednym stole.
Rozwiąż nierówność 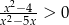 .
.
Podstawą ostrosłupa jest prostokąt o bokach 6 cm i 8 cm. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod katem 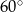 . Oblicz pole powierzchni ostrosłupa.
. Oblicz pole powierzchni ostrosłupa.
Z elementów zbioru 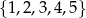 losujemy kolejno ze zwracaniem trzy:
losujemy kolejno ze zwracaniem trzy: 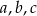 . Ile mamy możliwości wylosowania takiej trójki, aby utworzyła ona:
. Ile mamy możliwości wylosowania takiej trójki, aby utworzyła ona:
- ciąg arytmetyczny niemalejący?
- ciąg arytmetyczny?
- ciąg geometryczny?
Punkty 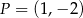 i
i 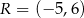 są dwoma sąsiednimi wierzchołkami kwadratu
są dwoma sąsiednimi wierzchołkami kwadratu 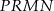 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 10 B) 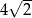 C) 8 D)
C) 8 D) 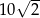
Punkty 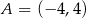 i
i 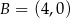 są sąsiednimi wierzchołkami kwadratu
są sąsiednimi wierzchołkami kwadratu 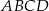 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 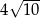 B)
B) 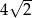 C)
C) 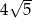 D)
D) 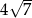
W układzie współrzędnych narysuj okrąg o równaniu 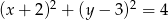 oraz zaznacz punkt
oraz zaznacz punkt 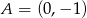 . Prosta o równaniu
. Prosta o równaniu 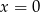 jest jedną ze stycznych do tego okręgu przechodzących przez punkt
jest jedną ze stycznych do tego okręgu przechodzących przez punkt 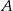 . Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt
. Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt 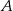 .
.
Wyznacz te wartości parametru 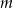 , dla których równanie
, dla których równanie 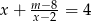 ma
ma
- dokładnie jedno rozwiązanie;
- dwa różne rozwiązania
W kartezjańskim układzie współrzędnych 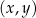 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 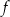 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 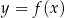 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
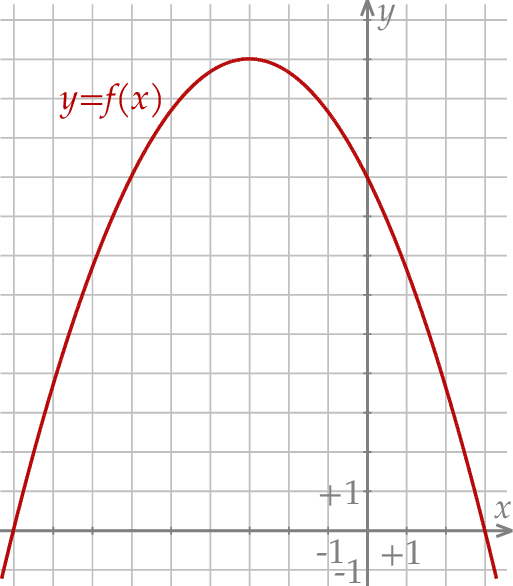
Zbiorem wartości funkcji 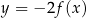 jest przedział
jest przedział
A) 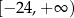 B)
B) ![(− ∞ ,12]](https://img.zadania.info/zad/9642145/HzadT6x.png) C)
C) ![(− ∞ ,− 12]](https://img.zadania.info/zad/9642145/HzadT7x.png) D)
D) 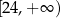
Dane są wierzchołki trójkąta 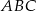 :
: 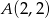 ,
, 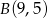 i
i 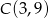 . Z wierzchołka
. Z wierzchołka 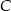 poprowadzono wysokość tego trójkąta, która przecina bok
poprowadzono wysokość tego trójkąta, która przecina bok 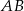 w punkcie
w punkcie 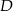 . Wyznacz równanie prostej przechodzącej przez punkt
. Wyznacz równanie prostej przechodzącej przez punkt 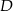 i równoległej do boku
i równoległej do boku 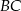 .
.
Wykres funkcji 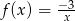 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i IV B) II i III C) I i III D) I i II
Wykres funkcji 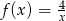 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i IV B) II i III C) I i III D) I i II
Wykres funkcji 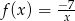 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i III B) II i IV C) I i III D) I i II
Wykres funkcji 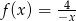 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) I i II B) II i III C) I i III D) II i IV
Ile rozwiązań posiada równanie: 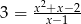 ?
?
A) 0 B) 1 C) 2 D) 3
Ile rozwiązań posiada równanie: 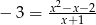 ?
?
A) 3 B) 2 C) 1 D) 0
Tomek i Marek chcą wejść docelowo na szczyt 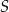 pewnej góry. W chwili początkowej znajdują się w punkcie
pewnej góry. W chwili początkowej znajdują się w punkcie 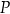 położonym na stoku góry dokładnie na północ od szczytu na wysokości
położonym na stoku góry dokładnie na północ od szczytu na wysokości 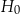 metrów n.p.m. Tomek i Marek chcą dotrzeć do bazy
metrów n.p.m. Tomek i Marek chcą dotrzeć do bazy 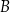 znajdującej się dokładnie na południe od szczytu na przeciwległym południowym stoku góry na wysokości
znajdującej się dokładnie na południe od szczytu na przeciwległym południowym stoku góry na wysokości 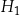 metrów n.p.m., a następnie z bazy wejść na szczyt leżący na wysokości
metrów n.p.m., a następnie z bazy wejść na szczyt leżący na wysokości 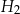 metrów n.p.m. (zobacz rysunek).
metrów n.p.m. (zobacz rysunek).
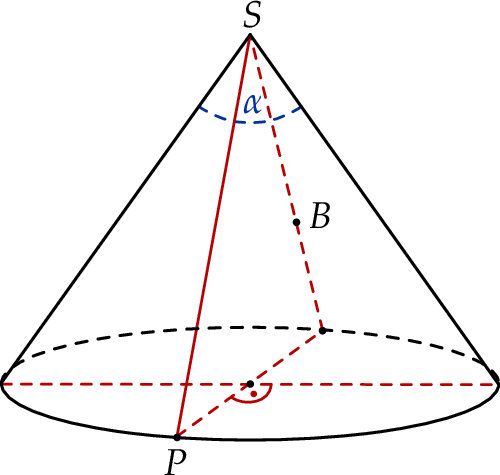
Oblicz długość najkrótszej drogi, jaką muszą pokonać, aby dotrzeć do bazy. Przyjmij, że góra jest stożkiem o kącie rozwarcia  .
.
W trójkącie 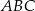 dane są:
dane są: 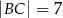 ,
, 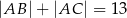 ,
, 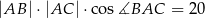 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
W ciągu arytmetycznym 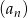 , dla
, dla 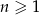 , dane są
, dane są 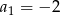 oraz różnica
oraz różnica 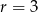 . Oblicz największe
. Oblicz największe  takie, że
takie, że 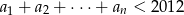 .
.
W ciągu arytmetycznym 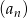 , dla
, dla 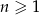 , dane są
, dane są 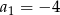 oraz różnica
oraz różnica 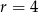 . Wyznacz największe
. Wyznacz największe  takie, że
takie, że 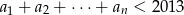 .
.
Proste o równaniach 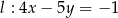 i
i 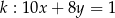
A) są równoległe B) są prostopadłe
C) przecinają się w punkcie 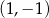 D) przecinają się w punkcie
D) przecinają się w punkcie 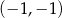
Proste o równaniach 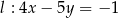 i
i 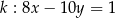
A) są równoległe B) są prostopadłe
C) przecinają się w punkcie 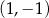 D) przecinają się w punkcie
D) przecinają się w punkcie 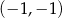
Proste o równaniach 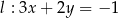 i
i 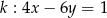
A) przecinają się w punkcie 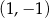 B) przecinają się w punkcie
B) przecinają się w punkcie 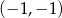
C) są równoległe D) są prostopadłe
Czas 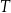 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 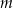 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
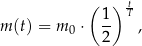
gdzie:
-
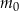 – masa przyjętej dawki leku,
– masa przyjętej dawki leku, -
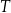 – czas półtrwania leku,
– czas półtrwania leku, -
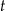 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pacjent otrzymuje co 4 dni o tej samej godzinie dawkę 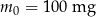 leku L. Czas półtrwania tego leku w organizmie jest równy
leku L. Czas półtrwania tego leku w organizmie jest równy 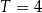 doby.
doby.
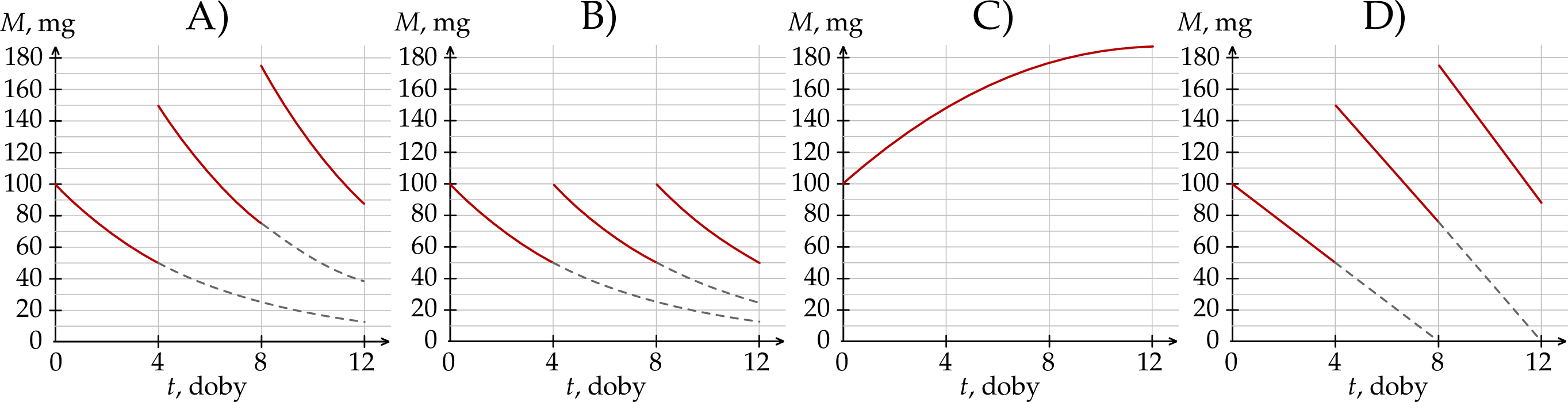
Wykres zależności masy 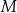 leku L w organizmie tego pacjenta od czasu
leku L w organizmie tego pacjenta od czasu 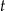 , liczonego od momentu przyjęcia przez pacjenta pierwszej dawki, przedstawiono na rysunku
, liczonego od momentu przyjęcia przez pacjenta pierwszej dawki, przedstawiono na rysunku
Czas 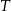 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 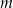 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
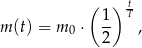
gdzie: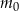 – masa przyjętej dawki leku
– masa przyjętej dawki leku 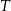 – czas półtrwania leku
– czas półtrwania leku 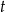 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pan Karol otrzymuje codziennie o godz. 12:00 dawkę 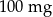 leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę
leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę 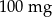 tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy
tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy 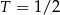 doby.
doby.
Wykres zależności masy 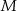 leku L w organizmie pana Karola od czasu
leku L w organizmie pana Karola od czasu  , liczonego od momentu przyjęcia przez niego pierwszej dawki, przedstawiono na rysunku
, liczonego od momentu przyjęcia przez niego pierwszej dawki, przedstawiono na rysunku
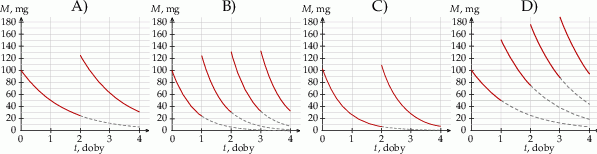
Ile razy trzeba rzucać trzema monetami, aby prawdopodobieństwo otrzymania co najmniej raz jednocześnie trzech orłów było większe od 0,8?
Na przekątnej 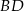 równoległoboku
równoległoboku 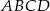 obrano dowolny punkt
obrano dowolny punkt 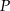 . Wykaż, że pola trójkątów
. Wykaż, że pola trójkątów 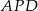 i
i 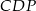 są równe.
są równe.
Na przekątnej 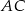 równoległoboku
równoległoboku 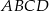 zaznaczono dowolny punkt
zaznaczono dowolny punkt 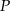 . Udowodnij, że pola trójkątów
. Udowodnij, że pola trójkątów 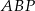 i
i 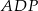 są równe.
są równe.

