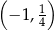Wykaż, że 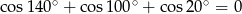 .
.
/Szkoła średnia
Wykonano pomiary wysokości czterech krzeseł i każde dwa rezultaty były różne. Adam zapisał wyniki w metrach i odchylenie standardowe jego danych było równe  . Bogdan zapisał te same wyniki w centymetrach i odchylenie standardowe jego danych było równe
. Bogdan zapisał te same wyniki w centymetrach i odchylenie standardowe jego danych było równe  . Wynika stąd, że
. Wynika stąd, że
A) 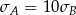 B)
B) 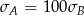 C)
C) 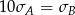 D)
D) 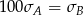
Wykonano pomiary wagi pięciu arbuzów i każde dwa rezultaty były różne. Agata zapisała wyniki w kilogramach i odchylenie standardowe jej danych było równe 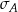 . Basia zapisała te same wyniki w gramach i odchylenie standardowe jej danych było równe
. Basia zapisała te same wyniki w gramach i odchylenie standardowe jej danych było równe 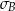 . Wynika stąd, że
. Wynika stąd, że
A) 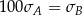 B)
B) 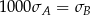 C)
C) 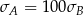 D)
D) 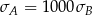
Ze zbioru 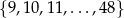 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3.
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie podzielna przez 3.
Oblicz ile liczb podzielnych przez 7 znajduje się w przedziale 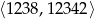 .
.
Cięciwy 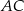 i
i 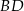 okręgu o środku
okręgu o środku 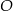 przecinają się w punkcie
przecinają się w punkcie 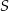 . Ponadto
. Ponadto 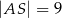 ,
, 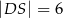 i
i 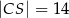 (zobacz rysunek).
(zobacz rysunek).
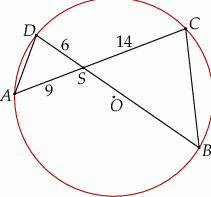
Długość odcinka 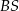 jest równa
jest równa
A) 24 B) 20 C) 21 D) 18
Wiadomo, że 1,5849 jest przybliżeniem liczby 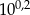 z zaokrągleniem do 4 miejsc po przecinku. Wyznacz przybliżenie liczby
z zaokrągleniem do 4 miejsc po przecinku. Wyznacz przybliżenie liczby 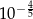 z zaokrągleniem do 3 miejsc po przecinku oraz przybliżenie liczby
z zaokrągleniem do 3 miejsc po przecinku oraz przybliżenie liczby 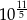 z zaokrągleniem do 1 miejsca po przecinku.
z zaokrągleniem do 1 miejsca po przecinku.
Prosta 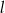 ma równanie
ma równanie 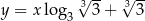 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 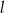 .
.
A) 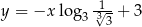 B)
B) 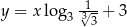
C) 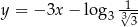 D)
D) 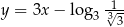
Rozważamy wszystkie liczby naturalne pięciocyfrowe zapisane przy użyciu cyfr 0, 3, 5, 7, 9, bez powtarzania jakiejkolwiek cyfry. Oblicz sumę wszystkich takich liczb.
Ciąg 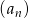 jest określony wzorem
jest określony wzorem
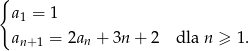
Oblicz średnią arytmetyczną liczb 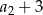 i
i 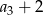 .
.
W kartezjańskim układzie współrzędnych  punkt
punkt 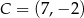 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 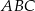 . Prosta
. Prosta 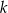 o równaniu
o równaniu 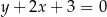 zawiera dwusieczną kąta
zawiera dwusieczną kąta 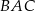 tego trójkąta. Okrąg
tego trójkąta. Okrąg 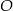 o równaniu
o równaniu 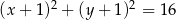 jest wpisany w ten trójkąt. Wyznacz współrzędne wierzchołków
jest wpisany w ten trójkąt. Wyznacz współrzędne wierzchołków 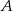 i
i 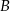 trójkąta
trójkąta 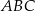 .
.
Rozwiąż równanie 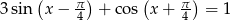 w przedziale
w przedziale 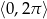 .
.
Rozwiąż równanie 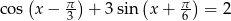 w przedziale
w przedziale 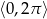 .
.
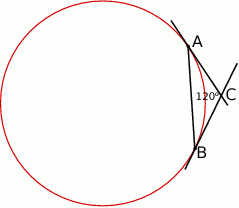
Przez punkty 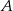 i
i 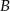 okręgu poprowadzono styczne, które przecięły się w punkcie
okręgu poprowadzono styczne, które przecięły się w punkcie  .
.
Wykaż, że jeżeli  , to cięciwa
, to cięciwa  ma długość równą długości promienia okręgu.
ma długość równą długości promienia okręgu.
Na bokach 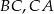 i
i 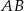 trójkąta
trójkąta 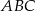 wybrano punkty
wybrano punkty 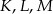 takie, że
takie, że
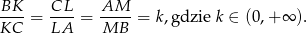
Oblicz stosunek pola trójkąta 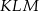 do pola trójkąta
do pola trójkąta 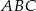 .
.
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem 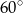 . Odległość spodka wysokości ostrosłupa od krawędzi bocznej jest równa 4. Oblicz objętość tego ostrosłupa.
. Odległość spodka wysokości ostrosłupa od krawędzi bocznej jest równa 4. Oblicz objętość tego ostrosłupa.
Wierzchołek paraboli 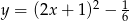 leży na prostej o równaniu
leży na prostej o równaniu
A) 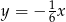 B)
B) 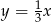 C)
C) 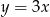 D)
D) 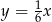
Wierzchołek paraboli 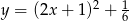 leży na prostej o równaniu
leży na prostej o równaniu
A) 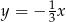 B)
B) 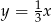 C)
C) 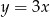 D)
D) 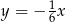
Rozwiązaniem równania 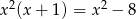 jest
jest
A) 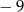 B)
B) 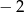 C) 2 D) 7
C) 2 D) 7
Rozwiązaniem równania 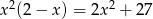 jest
jest
A) 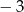 B)
B) 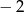 C) 3 D) 2
C) 3 D) 2
Czy istnieje taki wielokąt, który ma 2 razy więcej przekątnych niż boków?
Kąt  jest taki, że
jest taki, że 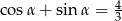 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 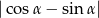 .
.
Największą liczbą będącą rozwiązaniem rzeczywistym równania 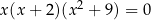 jest
jest
A) 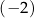 B) 0 C) 2 D) 3
B) 0 C) 2 D) 3
Do wykresu funkcji 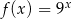 nie należy punkt
nie należy punkt
A) 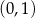 B)
B) 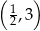 C)
C) 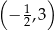 D)
D) 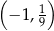
Do wykresu funkcji 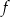 danej wzorem
danej wzorem 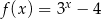 , należy punkt o współrzędnych
, należy punkt o współrzędnych
A) 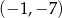 B)
B) 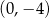 C)
C) 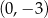 D)
D) 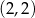
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem 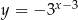 , należy punkt
, należy punkt
A) 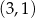 B)
B) 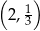 C)
C) 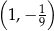 D)
D) 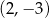
Do wykresu funkcji 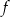 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  wzorem
wzorem 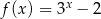 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 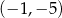 B)
B) 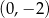 C)
C) 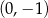 D)
D) 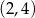
Do wykresu funkcji 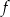 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  wzorem
wzorem 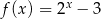 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 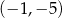 B)
B) 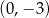 C)
C) 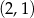 D)
D) 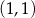
Do wykresu funkcji 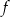 danej wzorem
danej wzorem 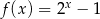 nie należy punkt o współrzędnych
nie należy punkt o współrzędnych
A) 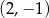 B)
B) 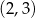 C)
C) 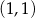 D)
D) 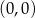
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem 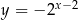 , należy punkt
, należy punkt
A) 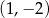 B)
B) 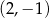 C)
C) 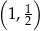 D)
D) 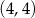
Do wykresu funkcji 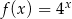 nie należy punkt
nie należy punkt
A) 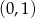 B)
B) 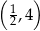 C)
C) 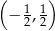 D)
D) 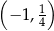
Do wykresu funkcji określonej wzorem 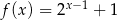 , należy punkt o współrzędnych
, należy punkt o współrzędnych
A) 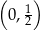 B)
B) 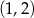 C)
C) 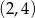 D)
D) 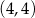
Do wykresu funkcji 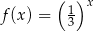 należy punkt
należy punkt
A) 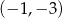 B)
B) 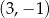 C)
C) 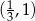 D)
D) 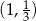
Do wykresu funkcji 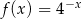 nie należy punkt
nie należy punkt
A) 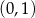 B)
B) 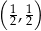 C)
C) 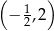 D)
D)