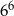Liczba pierwiastków wielomianu 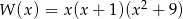 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
/Szkoła średnia
Liczba rzeczywistych rozwiązań równania 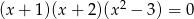 jest równa
jest równa
A) 0 B) 1 C) 2 D) 4
Równanie 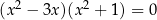 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Liczba pierwiastków wielomianu 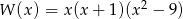 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba rzeczywistych rozwiązań równania 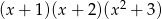 jest równa
jest równa
A) 0 B) 1 C) 2 D) 4
Równanie 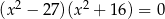 ma dokładnie
ma dokładnie
A) jedno rozwiązanie rzeczywiste.
B) dwa rozwiązania rzeczywiste.
C) trzy rozwiązania rzeczywiste.
D) cztery rozwiązania rzeczywiste.
Liczba pierwiastków wielomianu 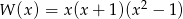 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Kąt  jest kątem ostrym i
jest kątem ostrym i 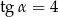 . Wyznacz sinus i cosinus tego kąta.
. Wyznacz sinus i cosinus tego kąta.
Kąt  jest ostry i
jest ostry i 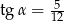 . Oblicz
. Oblicz 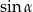 .
.
Kąt  jest ostry i
jest ostry i 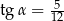 . Oblicz
. Oblicz 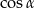 .
.
Dany jest czworokąt 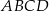 , w którym
, w którym 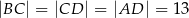 .
.
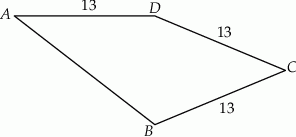
Przekątna 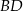 tego czworokąta ma długość 10 i jest prostopadła do boku
tego czworokąta ma długość 10 i jest prostopadła do boku 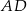 . Oblicz pole czworokąta
. Oblicz pole czworokąta 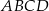 .
.
Funkcja kwadratowa 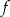 jest określona wzorem
jest określona wzorem 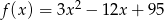 . Zatem wartość
. Zatem wartość 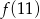 jest równa
jest równa
A) 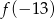 B)
B) 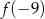 C)
C) 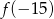 D)
D) 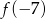
Rozwiąż równanie 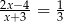 .
.
Znajdź najmniejszą i największą wartość funkcji 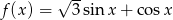 w przedziale
w przedziale 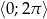 .
.
Znajdź najmniejszą i największą wartość funkcji 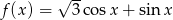 w przedziale
w przedziale 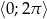 .
.
Liczba 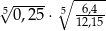 jest równa
jest równa
A) 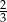 B) 1,5 C)
B) 1,5 C) 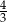 D)
D) 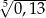
Wyznacz w zależności od parametru 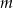 liczbę rozwiązań równania
liczbę rozwiązań równania 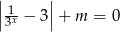 .
.
Niech 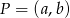 będzie dowolnym punktem wykresu funkcji
będzie dowolnym punktem wykresu funkcji 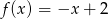 .
.
- Wyraź sumę odległości punktu
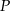 od osi układu współrzędnych jako funkcję zmiennej
od osi układu współrzędnych jako funkcję zmiennej  i naszkicuj wykres tej funkcji.
i naszkicuj wykres tej funkcji. - Znajdź współrzędne takiego punktu należącego do wykresu funkcji
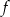 , którego suma odległości od osi układu współrzędnych jest równa 16.
, którego suma odległości od osi układu współrzędnych jest równa 16.
Do dwóch okręgów o promieniach długości 3 cm i 10 cm poprowadzono wspólną styczną tak, że okręgi znajdują się po różnych stronach tej stycznej. Odległość między środkami okręgów wynosi 39 cm. Oblicz długość odcinka między punktami styczności.
Liczba 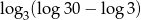 jest równa liczbie
jest równa liczbie
A) -1 B) 0 C) 1 D) 2
Liczba 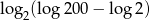 jest równa liczbie
jest równa liczbie
A) 1 B) 0 C) -1 D) 2
Liczba 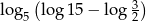 jest równa liczbie
jest równa liczbie
A) 1 B) -1 C) 0 D) 2
Napisz równanie okręgu, którego środek należy do osi 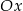 , i który przechodzi przez punkty
, i który przechodzi przez punkty 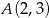 i
i 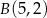 .
.
Napisz równanie okręgu, którego środek leży na prostej 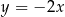 , i który przechodzi przez punkty
, i który przechodzi przez punkty 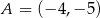 i
i 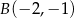 .
.
Wyznacz równanie okręgu przechodzącego przez punkty 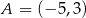 i
i 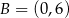 , którego środek leży na prostej o równaniu
, którego środek leży na prostej o równaniu 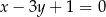 .
.
Na rysunku przedstawiony jest wykres funkcji 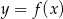 . Rozwiązaniem nierówności
. Rozwiązaniem nierówności 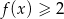 jest przedział
jest przedział
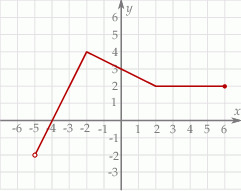
A) 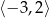 B)
B) 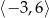 C)
C) 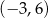 D)
D) 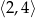
Na rysunku przedstawiony jest wykres funkcji  .
.
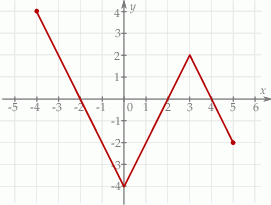
Maksymalnym zbiorem, w którym funkcja 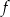 przyjmuje tylko wartości ujemne, jest
przyjmuje tylko wartości ujemne, jest
A) 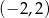 B)
B) 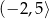 C)
C) 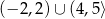 D)
D) 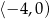
Na rysunku przedstawiony jest wykres funkcji 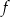 .
.
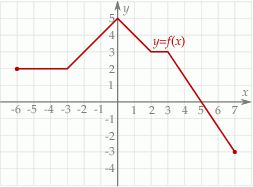
Przedziałem, w którym funkcja 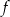 przyjmuje tylko wartości ujemne, jest
przyjmuje tylko wartości ujemne, jest
A) 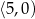 B)
B) 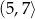 C)
C) 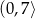 D)
D) 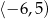
Na rysunku poniżej przedstawiony jest wykres funkcji 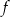 .
.
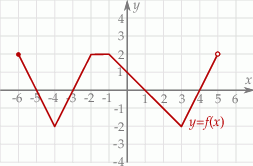
Funkcja ta przyjmuje wartości nieujemne dla
A) 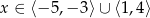 B)
B) 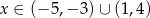
C) 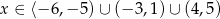 D)
D) 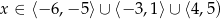
Wykaż, że jeżeli 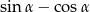 jest liczbą wymierną to wymierna jest również liczba
jest liczbą wymierną to wymierna jest również liczba 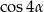 .
.
Miary kątów trójkąta prostokątnego tworzą ciąg arytmetyczny. Jeśli trójkąt ten będziemy obracać wokół dłuższej przyprostokątnej, to otrzymamy stożek, którego pole powierzchni bocznej wynosi 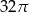 . Oblicz długości boków tego trójkąta.
. Oblicz długości boków tego trójkąta.
Suma długości wszystkich wysokości trójkąta 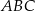 jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt
jest 9 razy większa od promienia okręgu wpisanego w ten trójkąt. Udowodnij, że trójkąt 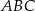 jest równoboczny.
jest równoboczny.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 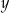 takich, że
takich, że 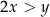 , spełniona jest nierówność
, spełniona jest nierówność
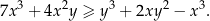
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Prawdziwe są równości
A) 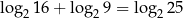 B)
B) 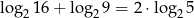
C) 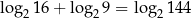 D)
D) 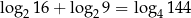
E) 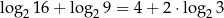 F)
F) 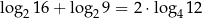
Dla jakich wartości parametru 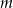 dziedziną funkcji
dziedziną funkcji 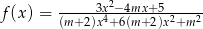 jest zbiór liczb rzeczywistych?
jest zbiór liczb rzeczywistych?
Liczba 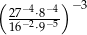 jest równa
jest równa
A) 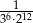 B)
B) 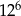 C)
C) 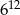 D)
D) 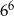
Liczba 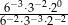 jest równa
jest równa
A) 6 B) 3 C) 24 D) 2
Liczba 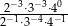 jest równa
jest równa
A) 1 B) 3 C) 24 D) 48
Liczba 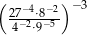 jest równa
jest równa
A) 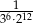 B)
B) 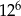 C)
C) 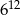 D)
D)