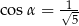Wyznacz promień okręgu wpisanego w trójkąt równoramienny o ramieniu długości 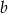 i kącie o mierze
i kącie o mierze  przy podstawie.
przy podstawie.
/Szkoła średnia
Wyznacz odległość punktu 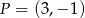 od prostej o równaniu
od prostej o równaniu 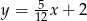 .
.
Oblicz wartość wyrażenia 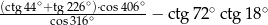 .
.
Wyznacz resztę z dzielenia wielomianu 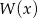 przez wielomian
przez wielomian 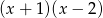 wiedząc, że
wiedząc, że 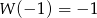 i
i 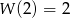 .
.
Wyznacz resztę z dzielenia wielomianu 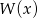 przez wielomian
przez wielomian 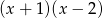 wiedząc, że
wiedząc, że 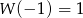 i
i 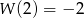 .
.
Wyznacz resztę z dzielenia wielomianu 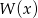 przez wielomian
przez wielomian 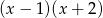 wiedząc, że
wiedząc, że 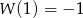 i
i 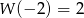 .
.
Funkcja 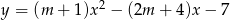 jest malejąca w zbiorze
jest malejąca w zbiorze 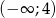 i rosnąca w zbiorze
i rosnąca w zbiorze 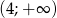 . Wyznacz parametr
. Wyznacz parametr 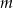 .
.
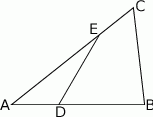
Na bokach 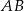 i
i 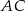 trójkąta
trójkąta 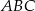 , który nie jest równoramienny, wybrano takie punkty
, który nie jest równoramienny, wybrano takie punkty 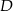 i
i 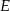 , że
, że 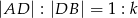 oraz
oraz 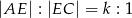 , dla
, dla 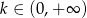 .
.
- Wyznacz wzór funkcji
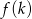 , która jest zdefiniowana jako stosunek pól trójkątów
, która jest zdefiniowana jako stosunek pól trójkątów 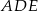 i
i 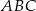 .
. - Wiedząc że
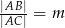 , dla
, dla 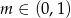 wyznacz wszystkie wartości parametru
wyznacz wszystkie wartości parametru 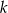 , dla których trójkąty
, dla których trójkąty 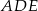 i
i 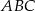 są podobne.
są podobne.
Oblicz objętość stożka, którego tworząca o długości 4 jest nachylona do płaszczyzny podstawy pod kątem 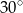 .
.
Liczba 99991 jest liczbą pierwszą. Liczba dzielników naturalnych liczby 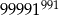 jest równa
jest równa
A) 1982 B) 990 C) 991 D) 992
Liczba 991 jest liczbą pierwszą. Liczba dzielników naturalnych liczby 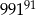 jest równa
jest równa
A) 182 B) 92 C) 91 D) 89
Oblicz pole rombu, którego jeden z kątów wewnętrznych wynosi 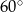 , a przekątna poprowadzona z wierzchołka tego kąta ma długość 20 cm.
, a przekątna poprowadzona z wierzchołka tego kąta ma długość 20 cm.
W prostokątnym układzie współrzędnych narysuj wykres funkcji
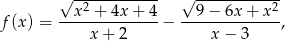
gdzie 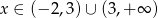 .
.
Liczba 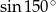 jest równa liczbie
jest równa liczbie
A) 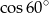 B)
B) 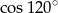 C)
C) 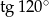 D)
D) 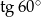
Liczba 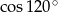 jest równa liczbie
jest równa liczbie
A) 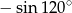 B)
B) 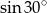 C)
C) 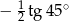 D)
D) 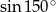
Liczba 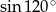 jest równa liczbie
jest równa liczbie
A) 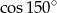 B)
B) 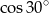 C)
C) 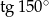 D)
D) 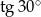
Dana jest funkcja 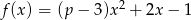 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 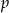 , dla których:
, dla których:
- największa wartość funkcji
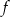 jest liczbą ujemną,
jest liczbą ujemną, - najmniejsza wartość funkcji
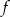 jest mniejsza od -2.
jest mniejsza od -2.
Uprość wyrażenie 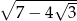 .
.
Jednym z rozwiązań równania 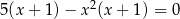 jest liczba
jest liczba
A) 1 B) 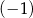 C) 5 D)
C) 5 D) 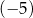
Koszt brutto wysłania SMS-a w usłudze Premium SMS wynosi 17,22 zł. Jaka jest wartość netto tego SMS-a, jeżeli koszt SMS-a obciążony jest 19% podatkiem dochodowym oraz 23% podatkiem VAT?
A) 7,12 zł B) 10,74 zł C) 25,20 zł D) 11,76 zł
Wielomian 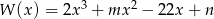 jest podzielny przez każdy z dwumianów
jest podzielny przez każdy z dwumianów 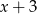 i
i 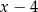 . Oblicz wartości współczynników
. Oblicz wartości współczynników  i
i 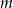 oraz rozwiąż nierówność
oraz rozwiąż nierówność 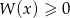 .
.
Wielomian określony wzorem 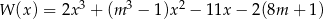 jest podzielny przez dwumian
jest podzielny przez dwumian 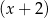 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 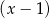 daje resztę 12. Oblicz
daje resztę 12. Oblicz 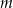 i dla wyznaczonej wartości
i dla wyznaczonej wartości 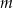 rozwiąż nierówność
rozwiąż nierówność 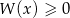 .
.
Wielomian określony wzorem 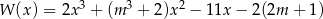 jest podzielny przez dwumian
jest podzielny przez dwumian 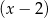 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 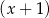 daje resztę 6. Oblicz
daje resztę 6. Oblicz 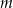 oraz pierwiastki wielomianu
oraz pierwiastki wielomianu 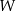 dla wyznaczonej wartości
dla wyznaczonej wartości 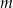 .
.
Wielomian określony wzorem 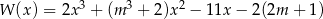 jest podzielny przez dwumian
jest podzielny przez dwumian 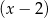 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 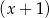 daje resztę 6. Oblicz
daje resztę 6. Oblicz 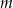 i dla wyznaczonej wartości
i dla wyznaczonej wartości 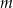 rozwiąż nierówność
rozwiąż nierówność 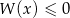 .
.
Pole powierzchni całkowitej sześcianu jest równe 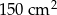 . Długość przekątnej podstawy tego sześcianu jest równa
. Długość przekątnej podstawy tego sześcianu jest równa
A) 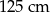 B)
B) 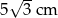 C)
C) 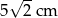 D)
D) 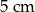
Pole powierzchni całkowitej sześcianu jest równe 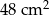 . Długość przekątnej podstawy tego sześcianu jest równa
. Długość przekątnej podstawy tego sześcianu jest równa
A) 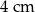 B)
B) 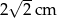 C)
C) 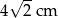 D)
D) 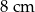
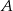 i
i 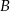 są takimi zdarzeniami losowymi zawartymi w
są takimi zdarzeniami losowymi zawartymi w 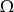 , że
, że 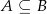 oraz
oraz 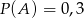 i
i 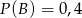 . Oblicz prawdopodobieństwo
. Oblicz prawdopodobieństwo 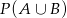 .
.
W trójkącie prostokątnym dane są kąty ostre: 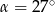 i
i 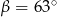 . Wtedy
. Wtedy 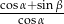 równa się
równa się
A) 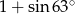 B)
B) 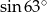 C) 1 D) 2
C) 1 D) 2
W trójkącie prostokątnym dane są kąty ostre: 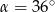 i
i 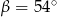 . Wtedy
. Wtedy 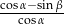 równa się
równa się
A) 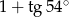 B)
B) 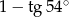 C) 1 D) 0
C) 1 D) 0
Wiadomo, że sinus kąta  trójkąta przedstawionego na rysunku jest równy
trójkąta przedstawionego na rysunku jest równy 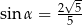 .
.
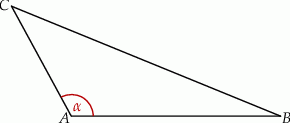
Wtedy
A) 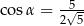 B)
B) 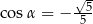 C)
C) 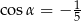 D)
D)