O zdarzeniach losowych 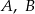 wiadomo, że:
wiadomo, że: 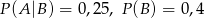 i
i 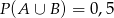 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 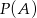 jest równe
jest równe
A) 0,1 B) 0,2 C) 0,3 D) 0,4
/Szkoła średnia
Trójkąt 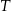 jest podobny do trójkąta
jest podobny do trójkąta 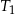 w skali
w skali 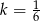 , a trójkąt
, a trójkąt 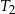 jest podobny do trójkąta
jest podobny do trójkąta 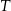 w skali
w skali 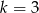 . Pole trójkąta
. Pole trójkąta 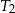 jest równe 24. Trójkąt
jest równe 24. Trójkąt 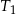 ma pole równe
ma pole równe
A) 12 B) 48 C) 72 D) 96
Trójkąt 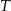 jest podobny do trójkąta
jest podobny do trójkąta 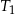 w skali
w skali 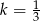 , a trójkąt
, a trójkąt 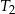 jest podobny do trójkąta
jest podobny do trójkąta 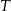 w skali
w skali 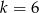 . Pole trójkąta
. Pole trójkąta 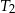 jest równe 32. Trójkąt
jest równe 32. Trójkąt 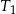 ma pole równe
ma pole równe
A) 128 B) 8 C) 16 D) 24
Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy  i wysokości
i wysokości 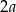 . Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środek ciężkości górnej podstawy. Oblicz pole otrzymanego przekroju.
. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środek ciężkości górnej podstawy. Oblicz pole otrzymanego przekroju.
Kąt  jest ostry i
jest ostry i 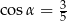 . Wtedy
. Wtedy
A) 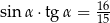 B)
B) 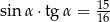 C)
C) 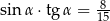 D)
D) 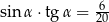
Kąt  jest ostry i
jest ostry i 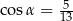 . Wtedy
. Wtedy
A) 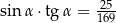 B)
B) 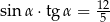 C)
C) 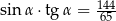 D)
D) 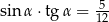
Rozwiąż nierówność 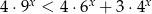 .
.
Kąt wpisany w okrąg o promieniu 6, który jest oparty na łuku długości 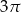 ma miarę
ma miarę
A) 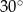 B)
B) 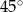 C)
C) 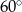 D)
D) 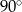
Kąt wpisany w okrąg o promieniu 5, który jest oparty na łuku długości 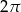 ma miarę
ma miarę
A) 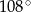 B)
B) 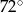 C)
C) 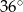 D)
D) 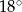
Kąt wpisany w okrąg o promieniu 12, który jest oparty na łuku długości 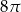 ma miarę
ma miarę
A) 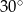 B)
B) 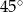 C)
C) 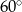 D)
D) 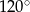
Kąt wpisany w okrąg o średnicy 8, który jest oparty na łuku długości 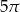 ma miarę
ma miarę
A) 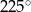 B)
B) 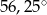 C)
C) 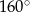 D)
D) 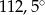
Iloraz ciągu geometrycznego 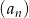 jest równy
jest równy 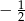 . Wynika stąd, że ciąg ten jest
. Wynika stąd, że ciąg ten jest
A) niemonotoniczny B) stały C) malejący D) rosnący
Liczba przekątnych jest równa liczbie boków w
A) prostokącie B) pięciokącie C) sześciokącie D) siedmiokącie
Liczba przekątnych jest o 3 większa niż liczba boków w
A) prostokącie B) pięciokącie C) sześciokącie D) siedmiokącie
Liczba przekątnych jest dwa razy większa niż liczba boków w
A) prostokącie B) pięciokącie C) sześciokącie D) siedmiokącie
Czy kąt zewnętrzny wielokąta foremnego może mieć miarę 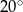 ?
?
Dany jest trójkąt prostokątny 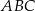 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 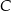 . Jeśli
. Jeśli 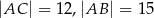 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A)  B)
B)  C)
C)  D)
D) 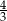
W trójkącie prostokątnym długość przeciwprostokątnej wynosi 8 i jednej z przyprostokątnych 6. Tangens mniejszego kąta ostrego tego trójkąta jest równy
A)  B)
B) 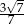 C)
C) 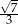 D)
D) 
Dany jest trójkąt prostokątny 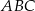 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 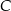 . Jeśli
. Jeśli 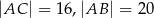 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A)  B)
B)  C)
C) 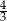 D)
D) 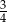
Dany jest trójkąt prostokątny 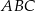 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 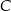 . Jeśli
. Jeśli 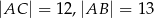 , to tangens najmniejszego kąta w tym trójkącie jest równy
, to tangens najmniejszego kąta w tym trójkącie jest równy
A) 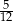 B)
B) 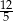 C)
C) 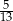 D)
D) 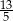
Jedna z przyprostokątnych trójkąta prostokątnego ma długość 15 cm, a przeciwprostokątna 17 cm. Tangens najmniejszego kąta w tym trójkącie jest równy:
A) 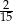 B)
B) 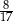 C)
C) 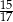 D)
D) 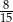
Obserwator stojący na płaskiej, poziomej powierzchni widzi pionową wieżę pod kątem 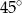 , a po zbliżeniu się do niej o 20m pod kątem
, a po zbliżeniu się do niej o 20m pod kątem 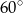 . Oblicz wysokość wieży, wynik zaokrąglij do 1cm.
. Oblicz wysokość wieży, wynik zaokrąglij do 1cm.
Dany jest nieskończony ciąg 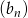 , dla którego
, dla którego 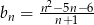 . Wobec tego wszystkie wyrazy tego ciągu są liczbami
. Wobec tego wszystkie wyrazy tego ciągu są liczbami
A) dodatnimi B) ujemnymi C) całkowitymi D) niewymiernymi
Dany jest nieskończony ciąg 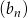 , dla którego
, dla którego 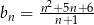 . Wobec tego wszystkie wyrazy tego ciągu są liczbami
. Wobec tego wszystkie wyrazy tego ciągu są liczbami
A) dodatnimi B) ujemnymi C) całkowitymi D) niewymiernymi
Dany jest nieskończony ciąg 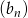 , dla którego
, dla którego 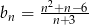 . Wobec tego wszystkie wyrazy tego ciągu są liczbami
. Wobec tego wszystkie wyrazy tego ciągu są liczbami
A) dodatnimi B) ujemnymi C) całkowitymi D) niewymiernymi
Określ wzorem rekurencyjnym ciąg którego pierwszy i drugi wyraz jest równy 3, a każdy następny jest iloczynem dwóch poprzednich.
Oblicz 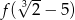 jeżeli
jeżeli 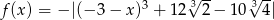 .
.
Ze zbioru dwudziestu czterech kolejnych liczb naturalnych od 1 do 24 losujemy jedną liczbę. Niech 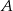 oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 24. Wtedy prawdopodobieństwo zdarzenia
oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 24. Wtedy prawdopodobieństwo zdarzenia 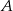 jest równe
jest równe
A) 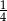 B)
B) 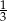 C)
C) 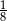 D)
D) 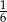
Ze zbioru trzydziestu kolejnych liczb naturalnych od 1 do 30 losujemy jedną liczbę. Niech 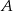 oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 30. Wtedy prawdopodobieństwo zdarzenia
oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 30. Wtedy prawdopodobieństwo zdarzenia 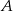 jest równe
jest równe
A) 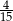 B)
B) 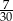 C)
C) 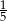 D)
D) 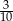
Iloczyn pierwszego i szóstego wyrazu malejącego ciągu arytmetycznego o wyrazach całkowitych jest równy 100. Przy dzieleniu wyrazu drugiego przez wyraz szósty otrzymujemy 3 i resztę 2. Oblicz, o ile jest mniejsza suma dwustu początkowych wyrazów o numerach parzystych od sumy dwustu początkowych wyrazów tego ciągu o numerach nieparzystych.
Wyznacz wszystkie liczby rzeczywiste  , spełniające równanie
, spełniające równanie
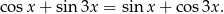
W trójkącie prostokątnym 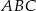 przyprostokątne mają długości
przyprostokątne mają długości 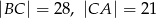 . Na boku
. Na boku 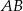 wybrano punkt
wybrano punkt 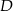 tak, że pole trójkąta
tak, że pole trójkąta 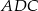 jest równe 126. Oblicz długość promienia okręgu opisanego na trójkącie
jest równe 126. Oblicz długość promienia okręgu opisanego na trójkącie 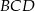 .
.
Funkcja liniowa 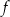 jest określona wzorem
jest określona wzorem 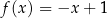 . Funkcja
. Funkcja 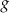 jest liniowa. W kartezjańskim układzie współrzędnych
jest liniowa. W kartezjańskim układzie współrzędnych 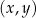 wykres funkcji
wykres funkcji 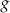 przechodzi przez punkt
przechodzi przez punkt 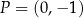 i jest prostopadły do wykresu funkcji
i jest prostopadły do wykresu funkcji 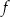 . Wzorem funkcji
. Wzorem funkcji 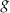 jest
jest
A) 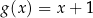 B)
B) 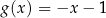 C)
C) 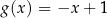 D)
D) 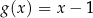
Podstawa 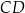 trapezu równoramiennego
trapezu równoramiennego 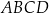 , który nie jest równoległobokiem, ma równanie
, który nie jest równoległobokiem, ma równanie 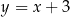 . Ponadto
. Ponadto 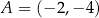 i
i 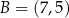 . Oś symetrii tego trapezu ma równanie
. Oś symetrii tego trapezu ma równanie
A) 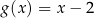 B)
B) 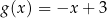 C)
C) 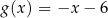 D)
D) 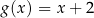
Funkcja liniowa 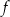 jest określona wzorem
jest określona wzorem 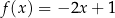 . Funkcja
. Funkcja 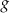 jest liniowa. W kartezjańskim układzie współrzędnych
jest liniowa. W kartezjańskim układzie współrzędnych 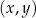 wykres funkcji
wykres funkcji 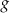 przechodzi przez punkt
przechodzi przez punkt 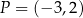 i jest prostopadły do wykresu funkcji
i jest prostopadły do wykresu funkcji 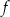 . Wzorem funkcji
. Wzorem funkcji 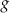 jest
jest
A) 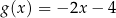 B)
B) 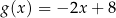 C)
C) 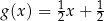 D)
D) 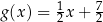
Pole trapezu jest równe 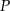 , a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
, a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.

