W prostokątnym układzie współrzędnych narysuj wykres funkcji
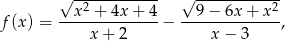
gdzie 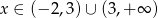 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W prostokątnym układzie współrzędnych narysuj wykres funkcji
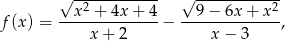
gdzie 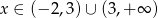 .
.
Liczba 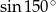 jest równa liczbie
jest równa liczbie
A) 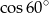 B)
B) 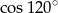 C)
C) 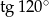 D)
D) 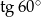
Liczba 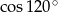 jest równa liczbie
jest równa liczbie
A) 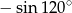 B)
B) 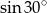 C)
C) 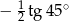 D)
D) 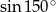
Liczba 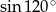 jest równa liczbie
jest równa liczbie
A) 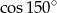 B)
B) 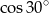 C)
C) 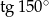 D)
D) 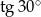
Dana jest funkcja 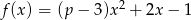 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 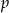 , dla których:
, dla których:
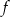 jest liczbą ujemną,
jest liczbą ujemną, 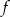 jest mniejsza od -2.
jest mniejsza od -2.Uprość wyrażenie 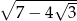 .
.
Jednym z rozwiązań równania 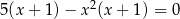 jest liczba
jest liczba
A) 1 B) 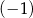 C) 5 D)
C) 5 D) 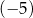
Koszt brutto wysłania SMS-a w usłudze Premium SMS wynosi 17,22 zł. Jaka jest wartość netto tego SMS-a, jeżeli koszt SMS-a obciążony jest 19% podatkiem dochodowym oraz 23% podatkiem VAT?
A) 7,12 zł B) 10,74 zł C) 25,20 zł D) 11,76 zł
Wielomian 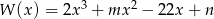 jest podzielny przez każdy z dwumianów
jest podzielny przez każdy z dwumianów 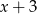 i
i 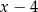 . Oblicz wartości współczynników
. Oblicz wartości współczynników  i
i 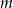 oraz rozwiąż nierówność
oraz rozwiąż nierówność 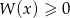 .
.
Wielomian określony wzorem 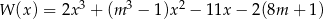 jest podzielny przez dwumian
jest podzielny przez dwumian 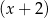 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 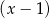 daje resztę 12. Oblicz
daje resztę 12. Oblicz 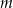 i dla wyznaczonej wartości
i dla wyznaczonej wartości 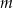 rozwiąż nierówność
rozwiąż nierówność 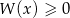 .
.
Wielomian określony wzorem 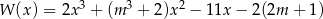 jest podzielny przez dwumian
jest podzielny przez dwumian 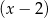 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 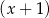 daje resztę 6. Oblicz
daje resztę 6. Oblicz 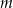 oraz pierwiastki wielomianu
oraz pierwiastki wielomianu 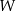 dla wyznaczonej wartości
dla wyznaczonej wartości 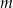 .
.
Wielomian określony wzorem 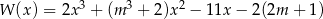 jest podzielny przez dwumian
jest podzielny przez dwumian 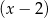 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 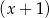 daje resztę 6. Oblicz
daje resztę 6. Oblicz 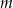 i dla wyznaczonej wartości
i dla wyznaczonej wartości 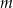 rozwiąż nierówność
rozwiąż nierówność 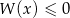 .
.
Pole powierzchni całkowitej sześcianu jest równe 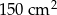 . Długość przekątnej podstawy tego sześcianu jest równa
. Długość przekątnej podstawy tego sześcianu jest równa
A) 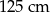 B)
B) 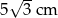 C)
C) 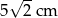 D)
D) 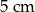
Pole powierzchni całkowitej sześcianu jest równe 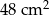 . Długość przekątnej podstawy tego sześcianu jest równa
. Długość przekątnej podstawy tego sześcianu jest równa
A) 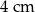 B)
B) 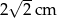 C)
C) 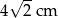 D)
D) 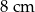
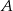 i
i 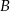 są takimi zdarzeniami losowymi zawartymi w
są takimi zdarzeniami losowymi zawartymi w 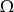 , że
, że 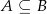 oraz
oraz 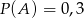 i
i 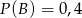 . Oblicz prawdopodobieństwo
. Oblicz prawdopodobieństwo 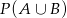 .
.
W trójkącie prostokątnym dane są kąty ostre: 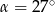 i
i 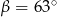 . Wtedy
. Wtedy 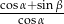 równa się
równa się
A) 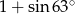 B)
B) 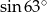 C) 1 D) 2
C) 1 D) 2
W trójkącie prostokątnym dane są kąty ostre: 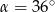 i
i 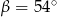 . Wtedy
. Wtedy 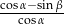 równa się
równa się
A) 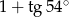 B)
B) 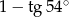 C) 1 D) 0
C) 1 D) 0
Wiadomo, że sinus kąta  trójkąta przedstawionego na rysunku jest równy
trójkąta przedstawionego na rysunku jest równy 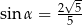 .
.
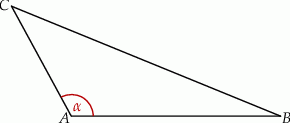
Wtedy
A) 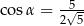 B)
B) 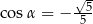 C)
C) 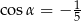 D)
D) 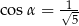
O zdarzeniach losowych 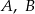 wiadomo, że:
wiadomo, że: 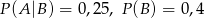 i
i 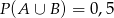 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 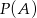 jest równe
jest równe
A) 0,1 B) 0,2 C) 0,3 D) 0,4
Trójkąt 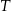 jest podobny do trójkąta
jest podobny do trójkąta 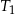 w skali
w skali 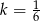 , a trójkąt
, a trójkąt 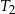 jest podobny do trójkąta
jest podobny do trójkąta 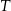 w skali
w skali 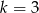 . Pole trójkąta
. Pole trójkąta 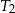 jest równe 24. Trójkąt
jest równe 24. Trójkąt 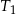 ma pole równe
ma pole równe
A) 12 B) 48 C) 72 D) 96
Trójkąt 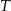 jest podobny do trójkąta
jest podobny do trójkąta 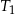 w skali
w skali 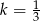 , a trójkąt
, a trójkąt 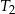 jest podobny do trójkąta
jest podobny do trójkąta 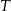 w skali
w skali 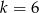 . Pole trójkąta
. Pole trójkąta 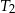 jest równe 32. Trójkąt
jest równe 32. Trójkąt 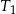 ma pole równe
ma pole równe
A) 128 B) 8 C) 16 D) 24
Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy  i wysokości
i wysokości 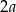 . Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środek ciężkości górnej podstawy. Oblicz pole otrzymanego przekroju.
. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środek ciężkości górnej podstawy. Oblicz pole otrzymanego przekroju.
Kąt  jest ostry i
jest ostry i 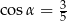 . Wtedy
. Wtedy
A) 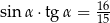 B)
B) 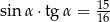 C)
C) 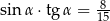 D)
D) 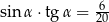
Kąt  jest ostry i
jest ostry i 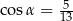 . Wtedy
. Wtedy
A) 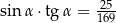 B)
B) 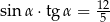 C)
C) 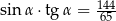 D)
D) 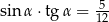
Rozwiąż nierówność 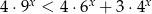 .
.
Kąt wpisany w okrąg o promieniu 6, który jest oparty na łuku długości 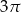 ma miarę
ma miarę
A) 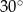 B)
B) 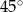 C)
C) 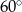 D)
D) 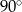
Kąt wpisany w okrąg o promieniu 5, który jest oparty na łuku długości 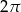 ma miarę
ma miarę
A) 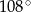 B)
B) 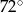 C)
C) 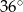 D)
D) 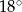
Kąt wpisany w okrąg o promieniu 12, który jest oparty na łuku długości 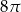 ma miarę
ma miarę
A) 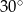 B)
B) 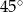 C)
C) 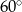 D)
D) 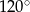
Kąt wpisany w okrąg o średnicy 8, który jest oparty na łuku długości 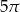 ma miarę
ma miarę
A) 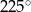 B)
B) 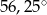 C)
C) 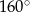 D)
D) 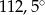
Iloraz ciągu geometrycznego 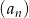 jest równy
jest równy 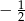 . Wynika stąd, że ciąg ten jest
. Wynika stąd, że ciąg ten jest
A) niemonotoniczny B) stały C) malejący D) rosnący
Liczba przekątnych jest równa liczbie boków w
A) prostokącie B) pięciokącie C) sześciokącie D) siedmiokącie
Liczba przekątnych jest o 3 większa niż liczba boków w
A) prostokącie B) pięciokącie C) sześciokącie D) siedmiokącie
Liczba przekątnych jest dwa razy większa niż liczba boków w
A) prostokącie B) pięciokącie C) sześciokącie D) siedmiokącie
Czy kąt zewnętrzny wielokąta foremnego może mieć miarę 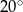 ?
?
