Do okręgów o równaniach 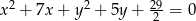 i
i 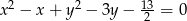 poprowadzono wspólną styczną. Oblicz długość odcinka łączącego punkty styczności. Rozważ wszystkie możliwości.
poprowadzono wspólną styczną. Oblicz długość odcinka łączącego punkty styczności. Rozważ wszystkie możliwości.
/Szkoła średnia
Dany jest romb, którego kąt ostry ma miarę 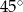 , a jego pole jest równe
, a jego pole jest równe 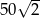 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
Dany jest romb, którego kąt ostry ma miarę 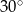 , a jego pole jest równe
, a jego pole jest równe 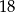 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
Na rysunku przedstawiony jest wykres funkcji 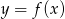 .
.
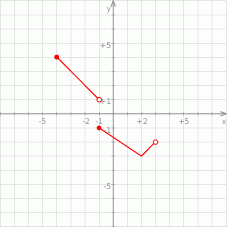
- Podaj zbiór wartości tej funkcji.
- Podaj dziedzinę tej funkcji.
- Wartość funkcji dla argumentu 2.
- Narysuj wykres funkcji
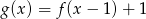 .
. - Narysuj wykres symetryczny do wykresu funkcji
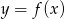 względem początku układu współrzędnych.
względem początku układu współrzędnych.
Na rysunku jest przedstawiony wykres funkcji 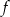 .
.
- Naszkicuj wykres funkcji
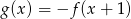 .
. - Określ dziedzinę
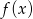 i
i 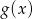 .
. - Podaj maksymalne przedziały, w których funkcja
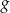 jest malejąca.
jest malejąca. - Podaj wartość funkcji
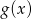 dla argumentu równego 2.
dla argumentu równego 2.
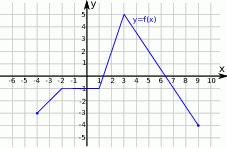
Na rysunku przedstawiony jest wykres funkcji 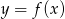 .
.
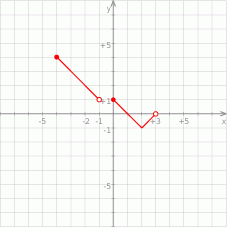
- Podaj zbiór wartości tej funkcji.
- Podaj dziedzinę tej funkcji.
- Wartość funkcji dla argumentu 2.
- Narysuj wykres funkcji
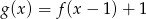 .
. - Narysuj wykres symetryczny do wykresu funkcji
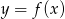 względem początku układu współrzędnych.
względem początku układu współrzędnych.
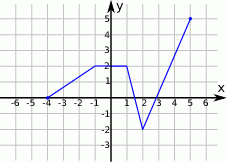
Na rysunku jest przedstawiony wykres funkcji 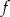 .
.
- Naszkicuj wykres funkcji
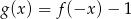 .
. - Określ dziedzinę
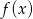 i
i 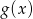 .
. - Podaj maksymalne przedziały, w których funkcja
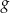 jest rosnąca.
jest rosnąca. - Podaj wartość funkcji
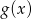 dla argumentu równego 1.
dla argumentu równego 1.
W graniastosłupie prawidłowym trójkątnym wysokość podstawy, krawędź podstawy i wysokość graniastosłupa tworzą ciąg geometryczny. Oblicz długość krawędzi podstawy graniastosłupa wiedząc, że jego objętość jest równa 108.
Oblicz wysokość trapezu o podstawach długości 18 i 14 oraz ramionach długości 3.
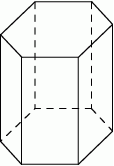
Spośród wierzchołków graniastosłupa sześciokątnego prostego losujemy jeden wierzchołek z dolnej podstawy i jeden wierzchołek z górnej podstawy. Oblicz prawdopodobieństwo tego, że wylosowane wierzchołki są końcami krawędzi bocznej graniastosłupa.
Wyznacz dziedzinę funkcji
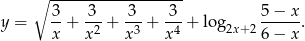
Średnią arytmetyczną liczb 5,5,7,3,9,9,4,4 jest liczba
A) 8 B) 5,5 C) 4 D) 5,75
Średnią arytmetyczną liczb 6,6,5,3,8,8,4,4 jest liczba
A) 6 B) 5,5 C) 4 D) 5,75
Średnią arytmetyczną liczb 3,3,5,6,8,9,4,4 jest liczba
A) 6 B) 5,25 C) 5 D) 5,75
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 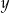 prawdziwa jest nierówność
prawdziwa jest nierówność
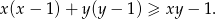
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 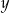 prawdziwa jest nierówność
prawdziwa jest nierówność
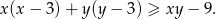
W trójkącie 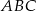 poprowadzono odcinek
poprowadzono odcinek 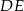 równoległy do boku
równoległy do boku 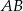 w ten sposób, że
w ten sposób, że 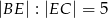 .
.
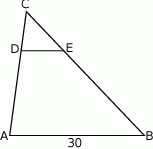
Jeżeli 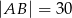 to długość odcinka
to długość odcinka 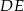 jest równa
jest równa
A) 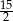 B) 6 C) 5 D)
B) 6 C) 5 D) 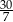
W trójkącie 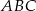 poprowadzono odcinek
poprowadzono odcinek 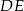 równoległy do boku
równoległy do boku 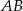 w ten sposób, że
w ten sposób, że 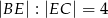 .
.
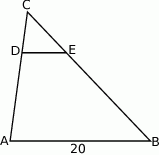
Jeżeli 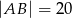 to długość odcinka
to długość odcinka 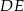 jest równa
jest równa
A) 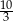 B) 4 C) 5 D)
B) 4 C) 5 D) 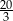
Wśród 115 osób przeprowadzono badania ankietowe, związane z zakupami w pewnym kiosku. W poniższej tabeli przedstawiono informacje o tym, ile osób kupiło bilety tramwajowe ulgowe oraz ile osób kupiło bilety tramwajowe normalne.
| Rodzaj kupionych biletów | Liczba osób |
| ulgowe | 76 |
| normalne | 41 |
Uwaga! 27 osób spośród ankietowanych kupiło oba rodzaje biletów.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że osoba losowo wybrana spośród ankietowanych nie kupiła żadnego biletu. Wynik przedstaw w formie nieskracalnego ułamka.
Wśród 93 pracowników pewnego zakładu pracy przeprowadzono badania ankietowe, związane z korzystaniem z dostępnych środków komunikacji miejskiej. W poniższej tabeli przedstawiono informacje o tym, ile osób korzysta z komunikacji tramwajowej, oraz ile osób korzysta z komunikacji autobusowej.
| Rodzaj komunikacji miejskiej | Liczba osób |
| tramwajowa | 43 |
| autobusowa | 47 |
Uwaga! 28 osób spośród ankietowanych korzysta zarówno z komunikacji autobusowej jak i tramwajowej.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba spośród ankietowanych nie korzysta z komunikacji miejskiej. Wynik przedstaw w formie nieskracalnego ułamka.
Rozwiąż nierówność 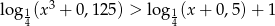 .
.
Na poniższym rysunku przedstawiono łamaną  , która jest wykresem funkcji
, która jest wykresem funkcji 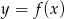 .
.
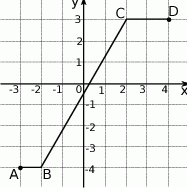
Korzystając z tego wykresu
- zapisz w postaci przedziału zbiór wartości funkcji
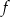 ,
, - podaj wartość funkcji
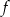 dla argumentu
dla argumentu 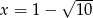 ,
, - wyznacz równanie prostej
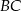 ,
, - oblicz długość odcinka
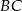 .
.
Dany jest ciąg arytmetyczny 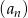 o różnicy
o różnicy 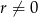 i pierwszym wyrazie
i pierwszym wyrazie 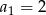 . Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.
. Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.
Oblicz prawdopodobieństwo, że losowo wybrana liczba trzycyfrowa ma wszystkie cyfry różne.
Rozwiąż graficznie i algebraicznie układ równań
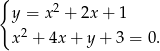
Wskaż równość prawdziwą.
A) 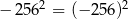 B)
B) 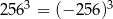
C) 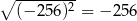 D)
D) 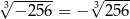
Wskaż równość fałszywą.
A) 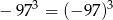 B)
B) 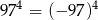 C)
C) 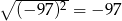 D)
D) 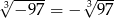
Liczby 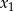 i
i 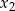 są pierwiastkami równania
są pierwiastkami równania 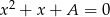 , a liczby
, a liczby 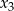 i
i 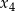 są pierwiastkami równania
są pierwiastkami równania 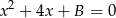 . Wiadomo, że ciąg
. Wiadomo, że ciąg 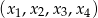 jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz
jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz 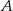 i
i 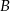 .
.
Dziedziną funkcji 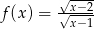 jest przedział
jest przedział
A) 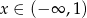 B)
B) 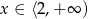 C)
C) 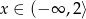 D)
D) 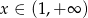
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 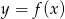 , której dziedziną jest zbiór
, której dziedziną jest zbiór 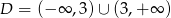 .
.
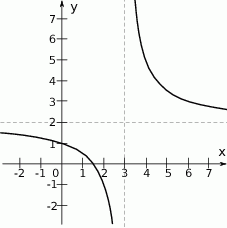
Równanie 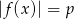 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 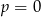 lub
lub 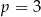 .
.
B) w dwóch przypadkach: 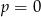 lub
lub 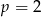 .
.
C) tylko wtedy, gdy 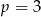 .
.
D) tylko wtedy, gdy 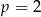 .
.
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 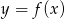 , której dziedziną jest zbiór
, której dziedziną jest zbiór 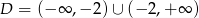 .
.
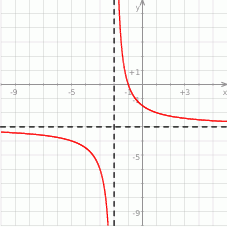
Równanie 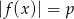 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 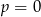 lub
lub 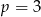 .
.
B) w dwóch przypadkach: 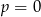 lub
lub 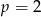 .
.
C) tylko wtedy, gdy 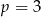 .
.
D) tylko wtedy, gdy 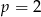 .
.

