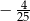Pole prostokąta 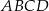 jest równe 90. Na bokach
jest równe 90. Na bokach 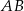 i
i 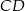 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 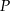 i
i 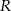 , takie, że
, takie, że 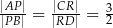 (zobacz rysunek)
(zobacz rysunek)
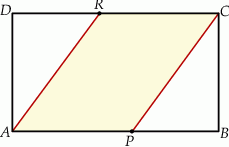
Pole czworokąta 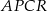 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Pole prostokąta 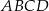 jest równe 90. Na bokach
jest równe 90. Na bokach 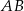 i
i 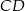 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 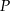 i
i 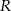 , takie, że
, takie, że 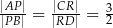 (zobacz rysunek)
(zobacz rysunek)

Pole czworokąta 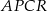 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Pole prostokąta 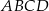 jest równe 90. Na bokach
jest równe 90. Na bokach 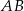 i
i 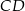 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 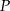 i
i 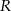 , takie, że
, takie, że 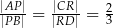 (zobacz rysunek)
(zobacz rysunek)
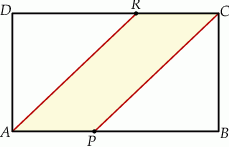
Pole czworokąta 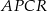 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Dany jest ośmiokąt foremny 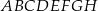 o boku długości 1.
o boku długości 1.
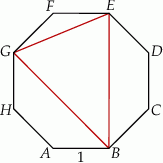
Niech 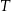 będzie środkiem odcinka
będzie środkiem odcinka 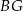 . Oblicz długość odcinka
. Oblicz długość odcinka 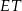 .
.
Z punktu 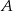 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 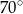 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 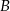 i
i 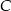 . Punkt
. Punkt 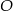 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 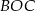 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 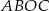 , jest równa
, jest równa
A) 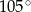 B)
B) 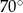 C)
C) 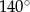 D)
D) 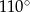
Z punktu 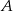 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 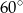 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 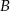 i
i 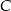 . Punkt
. Punkt 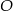 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 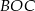 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 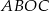 , jest równa
, jest równa
A) 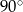 B)
B) 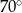 C)
C) 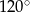 D)
D) 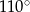
Z punktu 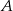 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 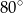 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 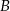 i
i 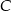 . Punkt
. Punkt 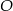 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 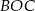 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 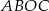 , jest równa
, jest równa
A) 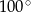 B)
B) 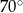 C)
C) 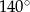 D)
D) 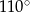
Końcami odcinka 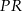 są punkty
są punkty 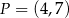 i
i 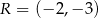 . Odległość punktu
. Odległość punktu 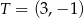 od środka odcinka
od środka odcinka 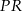 jest równa
jest równa
A) 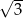 B)
B) 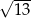 C)
C) 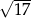 D)
D) 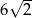
Końcami odcinka 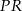 są punkty
są punkty 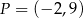 i
i 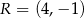 . Odległość punktu
. Odległość punktu 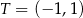 od środka odcinka
od środka odcinka 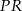 jest równa
jest równa
A) 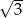 B)
B) 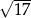 C)
C) 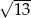 D)
D) 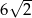
Wiedząc, że 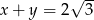 i
i 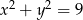 oblicz
oblicz 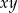 .
.
Czy kwadratową płytą o boku długości 2,2 m można całkowicie zakryć otwór w ziemi, który ma kształt stożka o wysokości 2 m i kącie rozwarcia 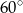 ?
?

Odpowiedź uzasadnij.
Wykaż, że jeżeli 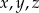 są długościami boków trójkąta to
są długościami boków trójkąta to 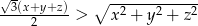 .
.
Uzasadnij, że jeżeli dwie dwusieczne trójkąta przecinają się pod kątem 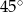 to trójkąt jest prostokątny.
to trójkąt jest prostokątny.
Punkt 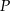 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 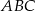 oraz
oraz 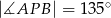 . Wykaż, że trójkąt
. Wykaż, że trójkąt 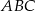 jest prostokątny.
jest prostokątny.
Podstawą ostrosłupa 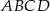 jest trójkąt równoramienny
jest trójkąt równoramienny 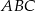 , w którym
, w którym 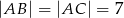 ,
, 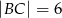 . Krawędzie boczne mają długości:
. Krawędzie boczne mają długości: 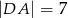 ,
, 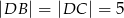 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Liczby 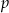 i
i 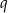 są pierwiastkami równania
są pierwiastkami równania 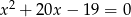 . Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia
. Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia 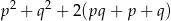 .
.
Liczby 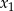 i
i 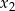 są pierwiastkami równania
są pierwiastkami równania 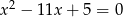 . Oblicz
. Oblicz 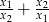 .
.
Liczby 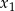 i
i 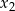 są pierwiastkami równania
są pierwiastkami równania 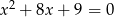 . Oblicz
. Oblicz 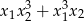 .
.
Liczby 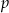 i
i 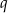 są pierwiastkami równania
są pierwiastkami równania 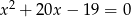 . Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia
. Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia 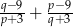 .
.
Liczby 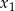 i
i 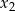 są pierwiastkami równania
są pierwiastkami równania 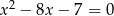 . Oblicz
. Oblicz 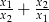 .
.
Liczby 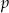 i
i 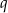 są pierwiastkami równania
są pierwiastkami równania 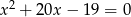 . Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia
. Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia 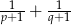 .
.
Na rysunku przedstawiono wykres funkcji 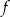 .
.
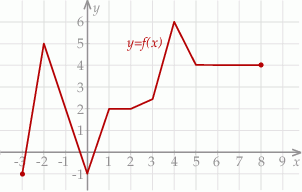
Najdłuższy przedział, na którym funkcja 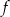 jest rosnąca to
jest rosnąca to
A) 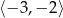 B)
B) 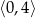 C)
C) 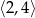 D)
D) 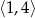
Na rysunku przedstawiono wykres funkcji 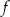 .
.
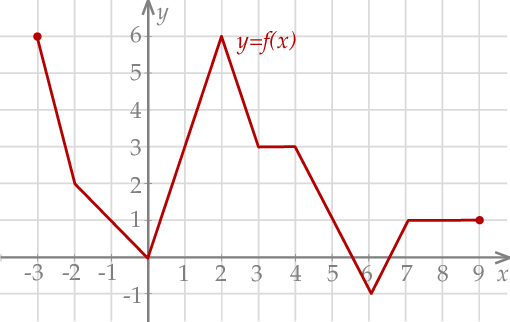
Najdłuższy przedział, na którym funkcja 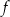 jest malejąca to
jest malejąca to
A) 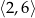 B)
B) 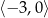 C)
C) 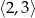 D)
D) 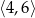
Wyznacz wszystkie wartości 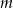 , dla których nierówność
, dla których nierówność 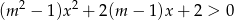 jest prawdziwa dla każdego
jest prawdziwa dla każdego 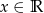 .
.
Liczby 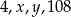 tworzą ciąg geometryczny, wtedy
tworzą ciąg geometryczny, wtedy
A) 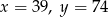 B)
B) 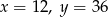 C)
C) 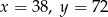 D)
D) 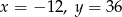
Liczby 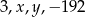 tworzą ciąg geometryczny, wtedy
tworzą ciąg geometryczny, wtedy
A) 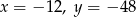 B)
B) 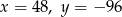 C)
C) 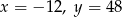 D)
D) 
Z kawałka materiału w kształcie czworokąta wypukłego o obwodzie 8m wycięto koło o polu 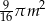 styczne do wszystkich boków czworokąta. Oblicz pole figury powstałej z tego czworokąta po wycięciu koła, z dokładnością do
styczne do wszystkich boków czworokąta. Oblicz pole figury powstałej z tego czworokąta po wycięciu koła, z dokładnością do 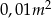 .
.
W trapezie 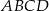 , w którym
, w którym 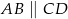 , dane są wierzchołki
, dane są wierzchołki 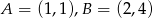 oraz punkt przecięcia przekątnych
oraz punkt przecięcia przekątnych 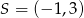 . Pole trapezu jest równe 36.
. Pole trapezu jest równe 36.
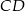 .
. 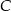 i
i 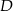 .
.Dane są dwie sumy algebraiczne 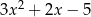 oraz
oraz 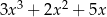 . Iloczyn tych sum jest równy
. Iloczyn tych sum jest równy
A) 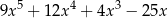 B)
B) 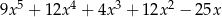
C) 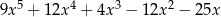 D)
D) 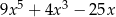
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 6 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 2. Przeciwprostokątna tego trójkąta ma długość
A) 24 B) 20 C) 14 D) 18
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 4. Wysokość ta dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 2. Przeciwprostokątna jest równa
A) 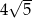 B)
B) 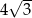 C) 10 D) 8
C) 10 D) 8
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 6 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 12. Przeciwprostokątna tego trójkąta ma długość
A) 15 B) 24 C) 16 D) 3
Wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego ma długość 8 i dzieli przeciwprostokątną na dwa odcinki, z których jeden ma długość 4. Przeciwprostokątna tego trójkąta ma długość
A) 20 B) 16 C) 8 D) 18
Na rysunku przedstawiono fragment wykresu pochodnej 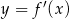 funkcji
funkcji 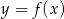 .
.
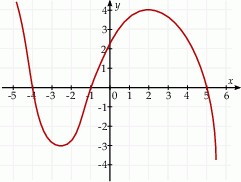
Funkcja 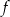 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A) 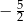 B)
B) 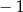 C)
C) 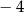 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 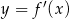 funkcji
funkcji 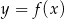 .
.
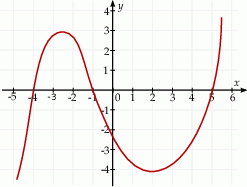
Funkcja 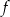 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A) 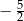 B)
B) 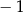 C)
C) 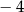 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 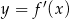 funkcji
funkcji 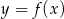 .
.
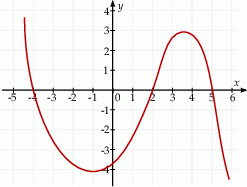
Funkcja 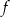 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A)  B)
B) 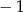 C)
C) 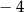 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 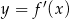 funkcji
funkcji 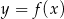 .
.
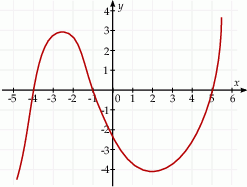
Funkcja 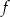 osiąga minimum lokalne dla argumentu
osiąga minimum lokalne dla argumentu
A) 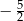 B)
B) 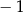 C)
C) 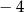 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 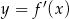 funkcji
funkcji 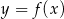 .
.
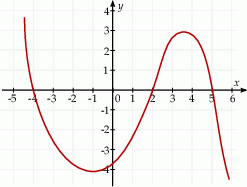
Funkcja 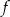 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A)  B)
B) 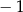 C)
C) 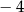 D) 2
D) 2
Na rysunku przedstawiono fragment wykresu pochodnej 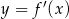 funkcji
funkcji 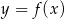 .
.
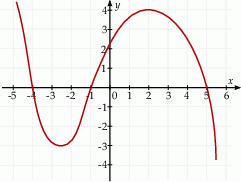
Funkcja 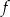 osiąga maksimum lokalne dla argumentu
osiąga maksimum lokalne dla argumentu
A) 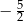 B)
B) 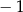 C)
C) 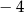 D) 2
D) 2
Ile jest liczb naturalnych siedmiocyfrowych, w których każde trzy cyfry stojące obok siebie są parami różne.
Kąt  jest ostry oraz
jest ostry oraz 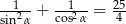 . Wartość wyrażenia
. Wartość wyrażenia 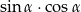 jest równa
jest równa
A)  B)
B)  C)
C) 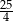 D)
D) 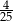
Kąt  jest rozwarty oraz
jest rozwarty oraz 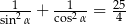 . Wartość wyrażenia
. Wartość wyrażenia 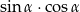 jest równa
jest równa
A) 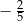 B)
B)  C)
C) 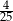 D)
D)