W trójkącie 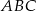 poprowadzono odcinek
poprowadzono odcinek 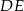 równoległy do boku
równoległy do boku 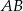 w ten sposób, że
w ten sposób, że 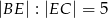 .
.
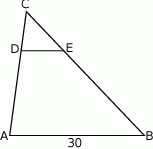
Jeżeli 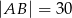 to długość odcinka
to długość odcinka 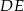 jest równa
jest równa
A) 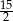 B) 6 C) 5 D)
B) 6 C) 5 D) 
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 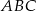 poprowadzono odcinek
poprowadzono odcinek 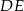 równoległy do boku
równoległy do boku 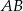 w ten sposób, że
w ten sposób, że 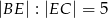 .
.

Jeżeli 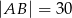 to długość odcinka
to długość odcinka 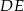 jest równa
jest równa
A) 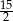 B) 6 C) 5 D)
B) 6 C) 5 D) 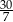
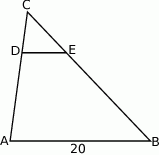
W trójkącie 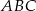 poprowadzono odcinek
poprowadzono odcinek 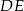 równoległy do boku
równoległy do boku 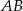 w ten sposób, że
w ten sposób, że 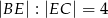 .
.
Jeżeli 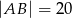 to długość odcinka
to długość odcinka 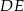 jest równa
jest równa
A) 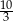 B) 4 C) 5 D)
B) 4 C) 5 D) 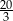
Wśród 115 osób przeprowadzono badania ankietowe, związane z zakupami w pewnym kiosku. W poniższej tabeli przedstawiono informacje o tym, ile osób kupiło bilety tramwajowe ulgowe oraz ile osób kupiło bilety tramwajowe normalne.
| Rodzaj kupionych biletów | Liczba osób |
| ulgowe | 76 |
| normalne | 41 |
Uwaga! 27 osób spośród ankietowanych kupiło oba rodzaje biletów.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że osoba losowo wybrana spośród ankietowanych nie kupiła żadnego biletu. Wynik przedstaw w formie nieskracalnego ułamka.
Wśród 93 pracowników pewnego zakładu pracy przeprowadzono badania ankietowe, związane z korzystaniem z dostępnych środków komunikacji miejskiej. W poniższej tabeli przedstawiono informacje o tym, ile osób korzysta z komunikacji tramwajowej, oraz ile osób korzysta z komunikacji autobusowej.
| Rodzaj komunikacji miejskiej | Liczba osób |
| tramwajowa | 43 |
| autobusowa | 47 |
Uwaga! 28 osób spośród ankietowanych korzysta zarówno z komunikacji autobusowej jak i tramwajowej.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba spośród ankietowanych nie korzysta z komunikacji miejskiej. Wynik przedstaw w formie nieskracalnego ułamka.
Rozwiąż nierówność 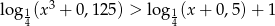 .
.
Na poniższym rysunku przedstawiono łamaną 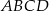 , która jest wykresem funkcji
, która jest wykresem funkcji 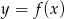 .
.
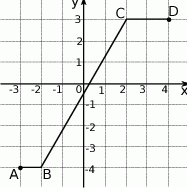
Korzystając z tego wykresu
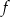 ,
, 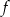 dla argumentu
dla argumentu 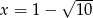 ,
, 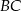 ,
, 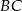 .
.Dany jest ciąg arytmetyczny 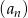 o różnicy
o różnicy 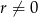 i pierwszym wyrazie
i pierwszym wyrazie 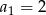 . Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.
. Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.
Oblicz prawdopodobieństwo, że losowo wybrana liczba trzycyfrowa ma wszystkie cyfry różne.
Rozwiąż graficznie i algebraicznie układ równań
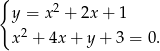
Wskaż równość prawdziwą.
A) 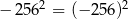 B)
B) 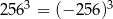
C) 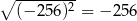 D)
D) 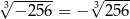
Wskaż równość fałszywą.
A) 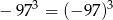 B)
B) 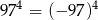 C)
C) 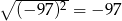 D)
D) 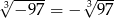
Liczby 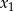 i
i 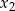 są pierwiastkami równania
są pierwiastkami równania 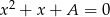 , a liczby
, a liczby 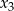 i
i 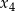 są pierwiastkami równania
są pierwiastkami równania 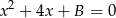 . Wiadomo, że ciąg
. Wiadomo, że ciąg 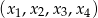 jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz
jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz 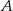 i
i 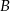 .
.
Dziedziną funkcji 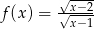 jest przedział
jest przedział
A) 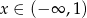 B)
B) 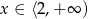 C)
C) 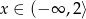 D)
D) 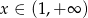
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 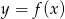 , której dziedziną jest zbiór
, której dziedziną jest zbiór 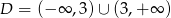 .
.
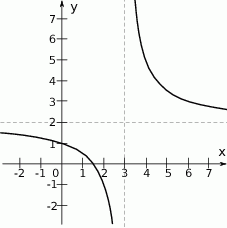
Równanie 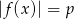 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 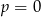 lub
lub 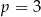 .
.
B) w dwóch przypadkach: 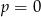 lub
lub 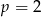 .
.
C) tylko wtedy, gdy 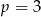 .
.
D) tylko wtedy, gdy 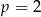 .
.
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 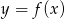 , której dziedziną jest zbiór
, której dziedziną jest zbiór 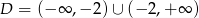 .
.
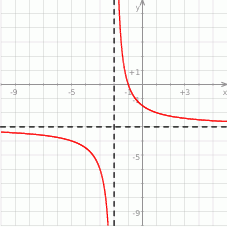
Równanie 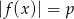 z niewiadomą
z niewiadomą  ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie
A) w dwóch przypadkach: 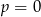 lub
lub 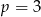 .
.
B) w dwóch przypadkach: 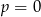 lub
lub 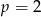 .
.
C) tylko wtedy, gdy 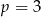 .
.
D) tylko wtedy, gdy 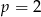 .
.
Pole prostokąta 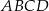 jest równe 90. Na bokach
jest równe 90. Na bokach 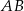 i
i 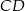 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 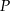 i
i 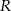 , takie, że
, takie, że 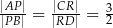 (zobacz rysunek)
(zobacz rysunek)
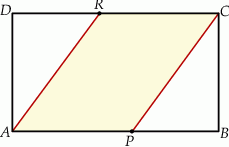
Pole czworokąta 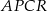 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Pole prostokąta 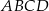 jest równe 90. Na bokach
jest równe 90. Na bokach 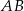 i
i 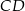 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 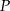 i
i 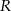 , takie, że
, takie, że 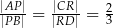 (zobacz rysunek)
(zobacz rysunek)
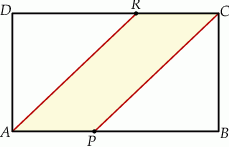
Pole czworokąta 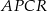 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Dany jest ośmiokąt foremny 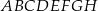 o boku długości 1.
o boku długości 1.
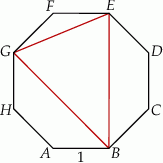
Niech 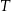 będzie środkiem odcinka
będzie środkiem odcinka 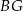 . Oblicz długość odcinka
. Oblicz długość odcinka 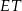 .
.
Z punktu 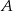 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 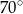 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 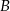 i
i 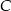 . Punkt
. Punkt 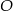 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 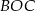 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 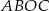 , jest równa
, jest równa
A) 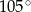 B)
B) 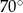 C)
C) 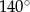 D)
D) 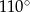
Z punktu 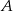 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 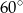 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 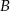 i
i 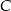 . Punkt
. Punkt 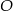 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 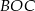 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 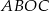 , jest równa
, jest równa
A) 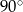 B)
B) 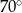 C)
C) 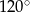 D)
D) 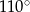
Z punktu 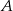 poprowadzono dwie styczne do okręgu, przecinające się pod kątem
poprowadzono dwie styczne do okręgu, przecinające się pod kątem 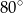 . Proste te są styczne do okręgu odpowiednio w punktach
. Proste te są styczne do okręgu odpowiednio w punktach 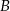 i
i 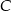 . Punkt
. Punkt 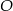 jest środkiem okręgu. Miara kąta środkowego
jest środkiem okręgu. Miara kąta środkowego 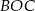 , który jest zarazem kątem czworokąta
, który jest zarazem kątem czworokąta 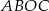 , jest równa
, jest równa
A) 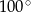 B)
B) 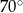 C)
C) 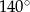 D)
D) 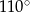
Końcami odcinka 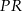 są punkty
są punkty 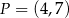 i
i 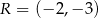 . Odległość punktu
. Odległość punktu 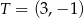 od środka odcinka
od środka odcinka 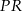 jest równa
jest równa
A) 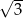 B)
B) 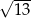 C)
C) 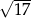 D)
D) 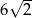
Końcami odcinka 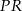 są punkty
są punkty 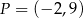 i
i 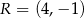 . Odległość punktu
. Odległość punktu 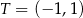 od środka odcinka
od środka odcinka 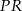 jest równa
jest równa
A) 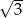 B)
B) 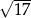 C)
C) 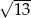 D)
D) 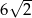
Wiedząc, że 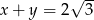 i
i 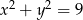 oblicz
oblicz 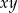 .
.
Czy kwadratową płytą o boku długości 2,2 m można całkowicie zakryć otwór w ziemi, który ma kształt stożka o wysokości 2 m i kącie rozwarcia 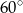 ?
?

Odpowiedź uzasadnij.
Wykaż, że jeżeli 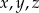 są długościami boków trójkąta to
są długościami boków trójkąta to 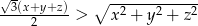 .
.
Uzasadnij, że jeżeli dwie dwusieczne trójkąta przecinają się pod kątem 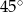 to trójkąt jest prostokątny.
to trójkąt jest prostokątny.
Punkt 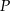 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 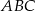 oraz
oraz 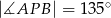 . Wykaż, że trójkąt
. Wykaż, że trójkąt 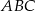 jest prostokątny.
jest prostokątny.
Podstawą ostrosłupa 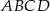 jest trójkąt równoramienny
jest trójkąt równoramienny 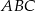 , w którym
, w którym 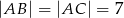 ,
, 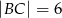 . Krawędzie boczne mają długości:
. Krawędzie boczne mają długości: 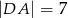 ,
, 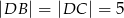 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
