Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
A) 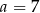 B)
B) 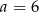 C)
C) 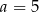 D)
D) 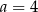
/Szkoła średnia
Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 7, 2, 4, 9, 1. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 7, 2, 4, 9, 1. Zatem
A) 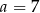 B)
B) 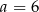 C)
C) 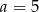 D)
D) 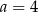
Jedno rozwiązanie ma równanie
A) 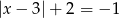 B)
B) 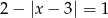 C)
C) 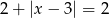 D)
D) 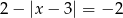
Dziewiąty wyraz ciągu geometrycznego jest równy 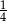 , a iloraz tego ciągu jest równy
, a iloraz tego ciągu jest równy 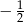 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) 16 B) 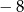 C)
C) 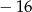 D) 8
D) 8
Długości boków trójkąta tworzą ciąg geometryczny. Jaki warunek spełniać musi iloraz tego ciągu?
Wykaż, że liczba 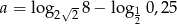 jest liczbą wymierną.
jest liczbą wymierną.
Wykaż, że liczba 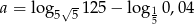 jest liczbą wymierną.
jest liczbą wymierną.
W trójkącie równoramiennym o bokach długości: 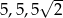 kąt przy podstawie ma miarę:
kąt przy podstawie ma miarę:
A) 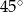 B)
B) 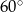 C)
C) 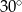 D)
D) 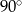
Dla jakich wartości parametru  równanie
równanie 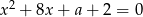 ma dwa różne pierwiastki jednakowych znaków?
ma dwa różne pierwiastki jednakowych znaków?
Długości boków trójkąta tworzą trzy kolejne wyrazy ciągu arytmetycznego o różnicy 1. Oblicz długości boków tego trójkąta, jeśli jego pole wynosi 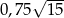 .
.
Wyrażenie 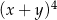 jest równe
jest równe
A) 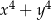 B)
B) 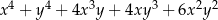
C) 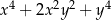 D)
D) 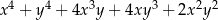
Wyrażenie 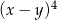 jest równe
jest równe
A) 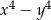 B)
B) 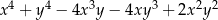
C) 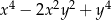 D)
D) 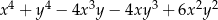
Funkcja 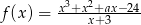 ma miejsce zerowe równe (-2). Wyznacz:
ma miejsce zerowe równe (-2). Wyznacz:
- wartość parametru
 ;
; - pozostałe miejsca zerowe funkcji;
- zbiór tych argumentów, dla których funkcja przyjmuje wartości nieujemne.
Rysunek przedstawia kształt obszaru zakreślanego przez wycieraczkę samochodową.
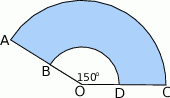
Wiedząc, że 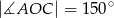 oraz
oraz 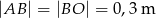 oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że
oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że 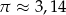 podaj wynik z dokładnością do
podaj wynik z dokładnością do 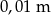 .
.
Suma wszystkich wyrazów ciągu danego wzorem 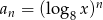 , gdzie
, gdzie 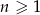 jest równa
jest równa 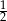 . Oblicz
. Oblicz  .
.
Suma przedziałów 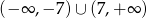 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 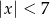 B)
B) 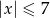 C)
C) 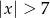 D)
D) 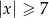
Suma przedziałów 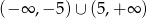 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 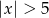 B)
B) 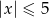 C)
C) 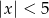 D)
D) 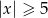
Suma przedziałów 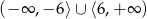 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 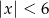 B)
B) 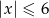 C)
C) 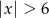 D)
D) 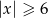
Podstawą ostrosłupa jest kwadrat 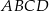 o boku długości 1. Wysokością tego ostrosłupa jest krawędź
o boku długości 1. Wysokością tego ostrosłupa jest krawędź 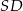 , a długość krawędzi
, a długość krawędzi 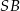 jest równa 2 (zobacz rysunek).
jest równa 2 (zobacz rysunek).
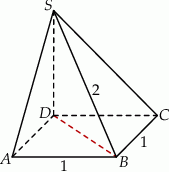
Różnica miar kątów 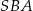 i
i 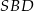 jest równa
jest równa
A) 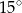 B)
B) 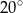 C)
C) 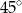 D)
D) 
W prostokątnym układzie współrzędnych zaznacz zbiór wszystkich punktów, których współrzędne spełniają warunek 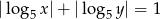 .
.
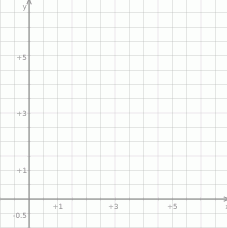
Wyznacz punkty wspólne wykresów 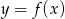 i
i 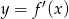 jeżeli
jeżeli 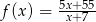 .
.
Wyznacz punkty wspólne wykresów 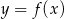 i
i 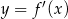 jeżeli
jeżeli 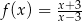 .
.
Jacek bawi się sześciennymi klockami o krawędzi 2 cm. Zbudował z nich jeden duży sześcian o krawędzi 8 cm i wykorzystał do tego wszystkie swoje klocki. Następnie zburzył budowlę i ułożył z tych klocków drugą bryłę – graniastosłup prawidłowy czworokątny. Wtedy okazało się, że został mu dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej ułożonej bryły do pola powierzchni całkowitej drugiej bryły i wynik podaj w postaci ułamka nieskracalnego.
Ania bawi się sześciennymi klockami o krawędzi 2 cm i buduje z nich bryły w kształcie prostokątów (prostopadłościanów o wysokości 1 klocka) w sposób przedstawiony na poniższym rysunku.
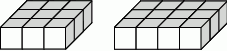
Najpierw Ania zbudowała z klocków pełen kwadrat o krawędzi 36 cm i wykorzystała do tego wszystkie swoje klocki. Następnie zburzyła tę budowlę i ułożyła z tych klocków prostokąt. Wtedy okazało się, że został jej dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej z ułożonych figur do pola powierzchni całkowitej drugiej figury.
W danym okręgu o środku 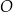 poprowadzono cięciwy
poprowadzono cięciwy 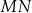 i
i 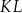 , które przecięły się w punkcie
, które przecięły się w punkcie 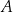 .
.

-
Wykaż, że trójkąty
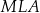 i
i 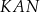 są podobne.
są podobne. -
Wiedząc, że
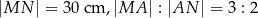 oraz
oraz 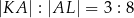 , oblicz długość cięciwy
, oblicz długość cięciwy 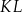 .
.
W trapezie równoramiennym, który nie jest równoległobokiem, ramię ma długość 7 cm, a przekątna 8 cm. Oblicz długości podstaw trapezu wiedząc, że odcinek łączący środki ramion trapezu ma długość 4 cm.
Rozwiąż nierówność 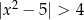 .
.

