Prosta przechodząca przez punkty 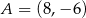 i
i 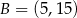 jest styczna do okręgu o środku w punkcie
jest styczna do okręgu o środku w punkcie 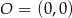 . Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą
. Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą 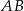 .
.
/Szkoła średnia
Prosta przechodząca przez punkty 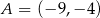 i
i 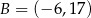 jest styczna do okręgu o środku w punkcie
jest styczna do okręgu o środku w punkcie 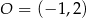 . Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą
. Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą 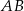 .
.
Z szuflady, w której znajduje się 10 różnych par rękawiczek wybieramy losowo cztery rękawiczki. Opisz zbiór wszystkich zdarzeń elementarnych, a następnie oblicz prawdopodobieństwa zdarzeń:
A – wśród wylosowanych rękawiczek nie będzie pary,
B – wśród wylosowanych rękawiczek będzie dokładnie jedna para.
W III wieku p.n.e władca Syrakuz, Hieron II, nakazał złotnikowi wykonać koronę ze sztaby ważącej 8,375 kg. Rzemieślnik wykonał koronę lecz władca podejrzewał, że artysta sprzeniewierzył część otrzymanego kruszcu. Hieron zwrócił się do Archimedesa, aby ten sprawdził, czy złotnik nie zastąpił części złota tańszym srebrem. Sławny fizyk zanurzył koronę w wodzie i sprawdził, że straciła ona pozornie na wadze 0,477 kg. Wiedząc, że złoto traci w wodzie pozornie 0,052 swojego ciężaru, z srebro 0,095, oblicz, ile złota, a ile srebra było w tej koronie. Wynik podaj z dokładnością do 0,001 kg.
Udowodnij, że dla każdej liczby naturalnej  , liczba
, liczba 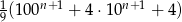 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Objętość walca wynosi 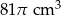 . Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
. Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
A) 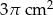 B)
B) 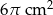 C)
C) 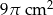 D)
D) 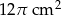
Na rysunku przedstawiony jest fragment wykresu funkcji logarytmicznej 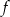 określonej wzorem
określonej wzorem 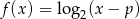 .
.
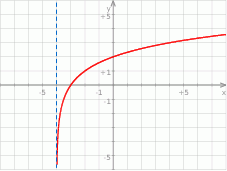
- Podaj wartość
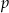 .
. - Narysuj wykres funkcji określonej wzorem
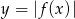 .
. - Podaj wszystkie wartości parametru
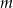 , dla których równanie
, dla których równanie 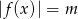 ma dwa rozwiązania o przeciwnych znakach.
ma dwa rozwiązania o przeciwnych znakach.
Punkty 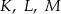 są środkami boków
są środkami boków 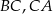 i
i 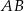 trójkąta
trójkąta 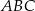 . Wykaż, że
. Wykaż, że
Ciąg 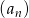 określony jest wzorem
określony jest wzorem 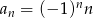 , gdzie
, gdzie 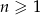 . Wówczas wyrażenie
. Wówczas wyrażenie 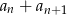 jest równe
jest równe
A) 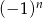 B)
B) 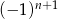 C)
C) 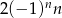 D)
D) 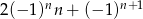
Na trapezie opisano okrąg o średnicy długości 25 cm. Dłuższa podstawa trapezu jest średnicą tego okręgu. Wiedząc, że przekątna tego trapezu ma długość 20 cm, oblicz pole tego trapezu.
Niech 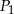 będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty
będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty 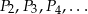 w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
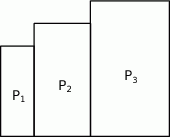
Wyznacz liczbę  , dla której obwód prostokąta
, dla której obwód prostokąta 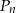 jest równy 246.
jest równy 246.
Rozwiąż układ równań 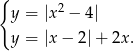
Objętość sześcianu jest równa 64. Pole powierzchni całkowitej tego sześcianu jest równe
A) 512 B) 384 C) 96 D) 16
Wszystkich par 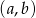 takich, że
takich, że 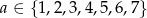 ,
, 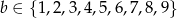 oraz suma
oraz suma 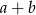 jest podzielna przez 3, jest
jest podzielna przez 3, jest
A) mniej niż 21 B) dokładnie 21 C) dokładnie 22 D) więcej niż 22
Stężenie roztworu początkowo wzrosło o 30%, a po 10 minutach wzrosło o dalsze 20%. W wyniku tych zmian stężenie wzrosło o
A) 44% B) 50% C) 56% D) 60%
Stężenie roztworu początkowo wzrosło o 25%, a po 10 minutach wzrosło o dalsze 20%. W wyniku tych zmian stężenie wzrosło o
A) 45% B) 50% C) 55% D) 60%
Stężenie roztworu początkowo wzrosło o 20%, a po 15 minutach wzrosło o dalsze 30%. W wyniku tych zmian stężenie wzrosło o
A) 44% B) 56% C) 50% D) 60%
W trapezie równoramiennym długość krótszej podstawy wynosi 9 cm, przekątnej 17 cm a ramienia 10 cm. Oblicz jego pole.
Funkcja 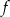 dana jest wzorem
dana jest wzorem
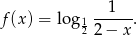
Określ dziedzinę funkcji 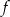 i naszkicuj jej wykres w przedziale
i naszkicuj jej wykres w przedziale 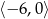 .
.
Kąt między przekątnymi sąsiednich ścian bocznych prostopadłościanu o podstawie kwadratowej jest równy 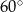 . Krawędź podstawy ma długość 12. Wyznacz pole powierzchni całkowitej tego prostopadłościanu i kąt nachylenia przekątnej ściany bocznej do płaszczyzny podstawy prostopadłościanu.
. Krawędź podstawy ma długość 12. Wyznacz pole powierzchni całkowitej tego prostopadłościanu i kąt nachylenia przekątnej ściany bocznej do płaszczyzny podstawy prostopadłościanu.
Dla jakich wartości parametru 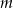 suma odwrotności pierwiastków równania
suma odwrotności pierwiastków równania 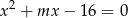 jest równa -4?
jest równa -4?
Udowodnij, że liczby 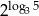 i
i 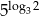 są równe.
są równe.
Uzasadnij, że 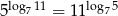 .
.
Dany jest trapez opisany na okręgu, którego kąty przy jednej podstawie są ostre, oraz którego pole jest równe 168. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów jeżeli ramiona trapezu mają długości 13 i 15.

