Funkcja 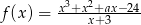 ma miejsce zerowe równe (-2). Wyznacz:
ma miejsce zerowe równe (-2). Wyznacz:
- wartość parametru
 ;
; - pozostałe miejsca zerowe funkcji;
- zbiór tych argumentów, dla których funkcja przyjmuje wartości nieujemne.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Funkcja 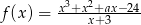 ma miejsce zerowe równe (-2). Wyznacz:
ma miejsce zerowe równe (-2). Wyznacz:
 ;
; Rysunek przedstawia kształt obszaru zakreślanego przez wycieraczkę samochodową.
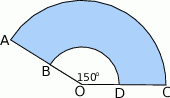
Wiedząc, że 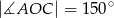 oraz
oraz 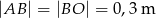 oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że
oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że 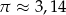 podaj wynik z dokładnością do
podaj wynik z dokładnością do 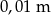 .
.
Suma wszystkich wyrazów ciągu danego wzorem 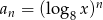 , gdzie
, gdzie 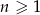 jest równa
jest równa 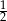 . Oblicz
. Oblicz  .
.
Suma przedziałów 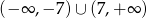 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 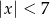 B)
B) 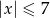 C)
C) 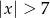 D)
D) 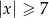
Suma przedziałów 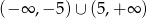 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 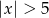 B)
B) 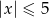 C)
C) 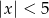 D)
D) 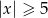
Suma przedziałów 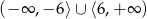 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 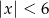 B)
B) 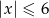 C)
C) 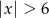 D)
D) 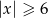
Podstawą ostrosłupa jest kwadrat 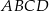 o boku długości 1. Wysokością tego ostrosłupa jest krawędź
o boku długości 1. Wysokością tego ostrosłupa jest krawędź 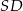 , a długość krawędzi
, a długość krawędzi 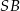 jest równa 2 (zobacz rysunek).
jest równa 2 (zobacz rysunek).
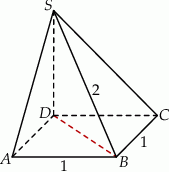
Różnica miar kątów 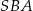 i
i 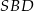 jest równa
jest równa
A) 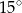 B)
B) 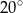 C)
C) 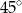 D)
D) 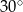
W prostokątnym układzie współrzędnych zaznacz zbiór wszystkich punktów, których współrzędne spełniają warunek 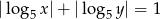 .
.
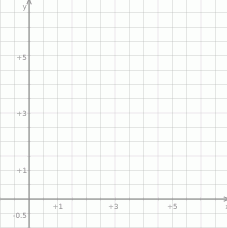
Wyznacz punkty wspólne wykresów 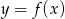 i
i 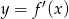 jeżeli
jeżeli 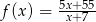 .
.
Wyznacz punkty wspólne wykresów 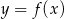 i
i 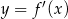 jeżeli
jeżeli 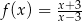 .
.
Jacek bawi się sześciennymi klockami o krawędzi 2 cm. Zbudował z nich jeden duży sześcian o krawędzi 8 cm i wykorzystał do tego wszystkie swoje klocki. Następnie zburzył budowlę i ułożył z tych klocków drugą bryłę – graniastosłup prawidłowy czworokątny. Wtedy okazało się, że został mu dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej ułożonej bryły do pola powierzchni całkowitej drugiej bryły i wynik podaj w postaci ułamka nieskracalnego.
Ania bawi się sześciennymi klockami o krawędzi 2 cm i buduje z nich bryły w kształcie prostokątów (prostopadłościanów o wysokości 1 klocka) w sposób przedstawiony na poniższym rysunku.
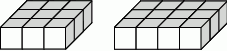
Najpierw Ania zbudowała z klocków pełen kwadrat o krawędzi 36 cm i wykorzystała do tego wszystkie swoje klocki. Następnie zburzyła tę budowlę i ułożyła z tych klocków prostokąt. Wtedy okazało się, że został jej dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej z ułożonych figur do pola powierzchni całkowitej drugiej figury.
W danym okręgu o środku 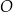 poprowadzono cięciwy
poprowadzono cięciwy 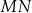 i
i 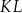 , które przecięły się w punkcie
, które przecięły się w punkcie 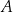 .
.

Wykaż, że trójkąty 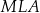 i
i 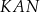 są podobne.
są podobne.
Wiedząc, że 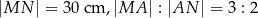 oraz
oraz 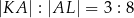 , oblicz długość cięciwy
, oblicz długość cięciwy 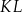 .
.
W trapezie równoramiennym, który nie jest równoległobokiem, ramię ma długość 7 cm, a przekątna 8 cm. Oblicz długości podstaw trapezu wiedząc, że odcinek łączący środki ramion trapezu ma długość 4 cm.
Rozwiąż nierówność 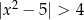 .
.
Prosta przechodząca przez punkty 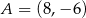 i
i 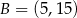 jest styczna do okręgu o środku w punkcie
jest styczna do okręgu o środku w punkcie 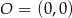 . Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą
. Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą 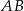 .
.
Prosta przechodząca przez punkty 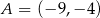 i
i 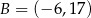 jest styczna do okręgu o środku w punkcie
jest styczna do okręgu o środku w punkcie 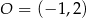 . Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą
. Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą 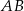 .
.
Z szuflady, w której znajduje się 10 różnych par rękawiczek wybieramy losowo cztery rękawiczki. Opisz zbiór wszystkich zdarzeń elementarnych, a następnie oblicz prawdopodobieństwa zdarzeń:
A – wśród wylosowanych rękawiczek nie będzie pary,
B – wśród wylosowanych rękawiczek będzie dokładnie jedna para.
W III wieku p.n.e władca Syrakuz, Hieron II, nakazał złotnikowi wykonać koronę ze sztaby ważącej 8,375 kg. Rzemieślnik wykonał koronę lecz władca podejrzewał, że artysta sprzeniewierzył część otrzymanego kruszcu. Hieron zwrócił się do Archimedesa, aby ten sprawdził, czy złotnik nie zastąpił części złota tańszym srebrem. Sławny fizyk zanurzył koronę w wodzie i sprawdził, że straciła ona pozornie na wadze 0,477 kg. Wiedząc, że złoto traci w wodzie pozornie 0,052 swojego ciężaru, z srebro 0,095, oblicz, ile złota, a ile srebra było w tej koronie. Wynik podaj z dokładnością do 0,001 kg.
Udowodnij, że dla każdej liczby naturalnej  , liczba
, liczba 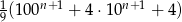 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Objętość walca wynosi 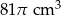 . Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
. Wysokość walca jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego walca jest równe
A) 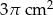 B)
B) 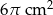 C)
C) 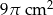 D)
D) 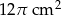
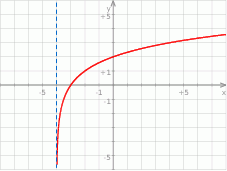
Na rysunku przedstawiony jest fragment wykresu funkcji logarytmicznej 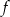 określonej wzorem
określonej wzorem 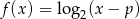 .
.
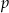 .
. 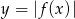 .
. 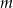 , dla których równanie
, dla których równanie 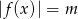 ma dwa rozwiązania o przeciwnych znakach.
ma dwa rozwiązania o przeciwnych znakach.Punkty 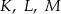 są środkami boków
są środkami boków 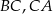 i
i 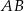 trójkąta
trójkąta 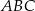 . Wykaż, że
. Wykaż, że
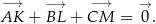
Ciąg 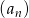 określony jest wzorem
określony jest wzorem 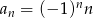 , gdzie
, gdzie 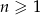 . Wówczas wyrażenie
. Wówczas wyrażenie 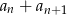 jest równe
jest równe
A) 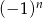 B)
B) 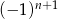 C)
C) 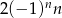 D)
D) 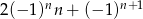
Na trapezie opisano okrąg o średnicy długości 25 cm. Dłuższa podstawa trapezu jest średnicą tego okręgu. Wiedząc, że przekątna tego trapezu ma długość 20 cm, oblicz pole tego trapezu.
