Wśród pewnej grupy pracowników przeprowadzono ankietę, w której odpowiadano na pytanie „Ile godzin dziennie spędzasz w pracy?”. Wyniki ankiety przedstawiono w tabeli.
| Liczba osób | 6 | 10 | 4 |
| Czas w godzinach | 7 | 8 | 9 |
Średnia liczba godzin spędzonych w pracy w tej grupie wynosi około
A) 10 B) 9 C) 8 D) 7

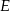 leży na ramieniu
leży na ramieniu 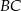 trapezu
trapezu 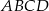 , w którym
, w którym 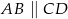 . Udowodnij, że
. Udowodnij, że 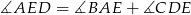 .
. 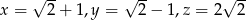 . Wtedy
. Wtedy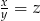
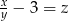
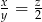
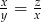
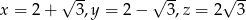 . Wtedy
. Wtedy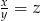
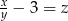
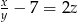
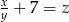
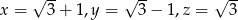 . Wtedy
. Wtedy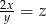
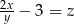
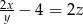
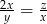
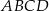 , którego bok
, którego bok 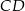 i przekątna
i przekątna 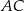 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 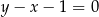 i
i 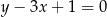 odpowiednio. Promień okręgu wpisanego w romb
odpowiednio. Promień okręgu wpisanego w romb 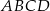 jest równy
jest równy 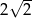 , a środek tego okręgu leży poniżej osi
, a środek tego okręgu leży poniżej osi 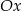 . Oblicz współrzędne punktu styczności okręgu wpisanego w romb
. Oblicz współrzędne punktu styczności okręgu wpisanego w romb 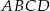 z jego bokiem
z jego bokiem 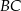 .
. 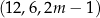 jest geometryczny. Dokończ zdanie tak, aby było prawdziwe. Ciąg
jest geometryczny. Dokończ zdanie tak, aby było prawdziwe. Ciąg 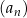 jest
jest 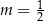 ,
,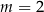 ,
,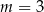 ,
,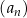 jest określony wzorem
jest określony wzorem 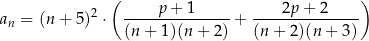
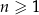 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 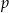 , dla których granica ciągu
, dla których granica ciągu 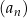 jest równa 12.
jest równa 12. 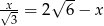 jest liczba
jest liczba 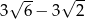
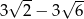
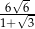
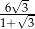
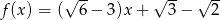 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba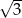
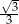
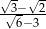
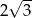
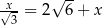 jest liczba
jest liczba 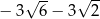
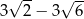
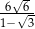
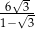
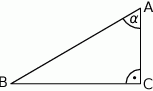
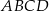 o boku długości 26, w którym przekątna
o boku długości 26, w którym przekątna 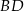 ma długość równą 20. Punkt
ma długość równą 20. Punkt 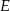 jest środkiem boku
jest środkiem boku 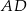 (zobacz rysunek).
(zobacz rysunek). 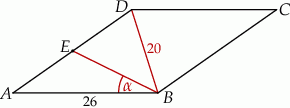
 , jaki odcinek
, jaki odcinek 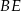 tworzy z bokiem
tworzy z bokiem 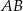 rombu
rombu 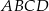 .
. 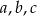 , gdzie
, gdzie 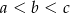 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 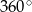 , otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
, otrzymujemy bryłę, której pole powierzchni całkowitej jest równe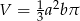
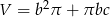
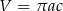
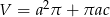
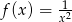 .
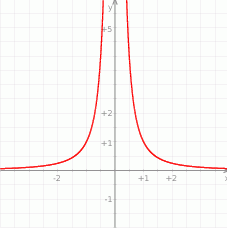
. 
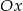 , która przecięła wykres tej funkcji w punktach
, która przecięła wykres tej funkcji w punktach 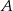 i
i 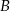 . Niech
. Niech 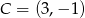 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 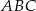 jest większe lub równe 2.
jest większe lub równe 2.  gdzie
gdzie  .
. 
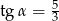 . Podaj wartości pozostałych funkcji trygonometrycznych kąta
. Podaj wartości pozostałych funkcji trygonometrycznych kąta  .
.  gdzie
gdzie  .
. 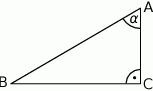
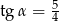 . Podaj wartości pozostałych funkcji trygonometrycznych kąta
. Podaj wartości pozostałych funkcji trygonometrycznych kąta  .
. 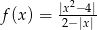 , a następnie określ, dla jakich wartości parametru
, a następnie określ, dla jakich wartości parametru 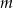 równanie
równanie 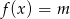 nie ma rozwiązania.
nie ma rozwiązania. 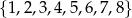 ustawiamy w przypadkowej kolejności (bez powtórzeń) tworząc liczbę ośmiocyfrową. Jakie jest prawdopodobieństwo otrzymania liczby, w której jednocześnie:
ustawiamy w przypadkowej kolejności (bez powtórzeń) tworząc liczbę ośmiocyfrową. Jakie jest prawdopodobieństwo otrzymania liczby, w której jednocześnie: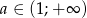 i
i 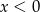 to prawdziwa jest nierówność
to prawdziwa jest nierówność 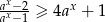 .
. 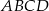 o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa 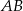 trapezu, o długości 12, jest średnicą tego okręgu. Przekątne
trapezu, o długości 12, jest średnicą tego okręgu. Przekątne 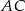 i
i 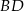 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 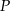 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 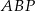 .
. 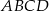 o ramieniu długości 7 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 7 wpisany jest w okrąg, przy czym dłuższa podstawa 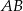 trapezu, o długości 14, jest średnicą tego okręgu. Przekątne
trapezu, o długości 14, jest średnicą tego okręgu. Przekątne 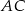 i
i 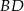 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 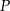 . Oblicz długość okręgu wpisanego w trójkąt
. Oblicz długość okręgu wpisanego w trójkąt 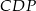 .
. 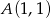 i równoległej do prostej danej równaniem
i równoległej do prostej danej równaniem 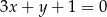 .
. 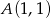 i równoległej do prostej danej równaniem
i równoległej do prostej danej równaniem 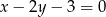 .
. 
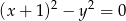 , jest
, jest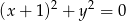 , jest
, jest okręgu wynosi:
okręgu wynosi: 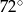
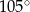
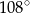
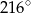
 długości okręgu jest równa
długości okręgu jest równa 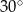
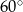
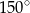
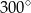
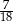 długości całego okręgu wynosi
długości całego okręgu wynosi 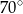
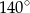
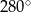
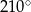
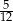 długości okręgu. Miara tego kąta wynosi
długości okręgu. Miara tego kąta wynosi 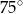
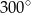
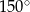
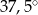
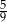 łuku okręgu?
łuku okręgu? 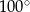
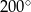
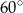
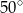
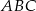 o wierzchołkach
o wierzchołkach 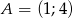 ,
, 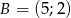 ,
, 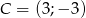 .
. 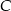 na bok
na bok 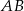 .
. 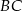 .
. 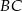 .
. 