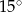Punkt 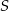 jest środkiem okręgu wpisanego w trójkąt równoramienny
jest środkiem okręgu wpisanego w trójkąt równoramienny 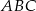 , w którym
, w którym 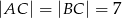 i
i 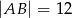 .
.
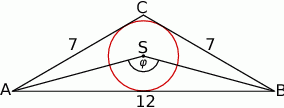
Wówczas miara 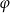 kąta
kąta 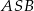 spełnia warunek
spełnia warunek
A) 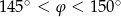 B)
B) 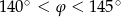 C)
C) 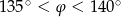 D)
D) 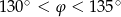
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkt 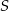 jest środkiem okręgu wpisanego w trójkąt równoramienny
jest środkiem okręgu wpisanego w trójkąt równoramienny 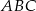 , w którym
, w którym 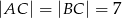 i
i 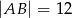 .
.

Wówczas miara 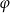 kąta
kąta 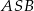 spełnia warunek
spełnia warunek
A) 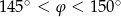 B)
B) 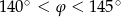 C)
C) 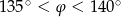 D)
D) 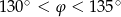
W trójkącie równoramiennym 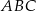 dane są
dane są 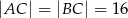 oraz
oraz 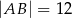 . Odcinek
. Odcinek 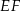 jest równoległy do podstawy
jest równoległy do podstawy 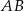 oraz
oraz 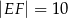 . Długość odcinka
. Długość odcinka 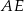 jest równa
jest równa
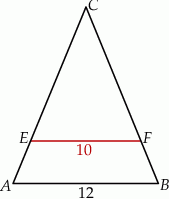
A) 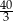 B)
B)  C)
C) 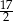 D)
D) 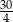
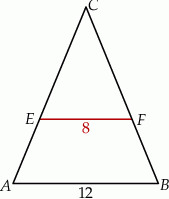
W trójkącie równoramiennym 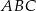 dane są
dane są 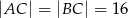 oraz
oraz 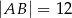 . Odcinek
. Odcinek 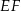 jest równoległy do podstawy
jest równoległy do podstawy 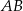 oraz
oraz 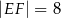 . Długość odcinka
. Długość odcinka 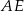 jest równa
jest równa
A) 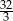 B)
B)  C)
C) 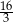 D)
D) 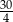
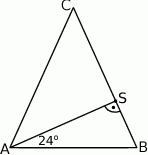
Dany jest równoramienny trójkąt 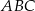 o kącie przy podstawie
o kącie przy podstawie 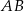 równym
równym 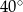 . Punkt
. Punkt 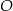 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 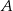 i
i 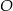 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 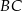 w punkcie
w punkcie 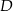 . Jeśli miara kąta
. Jeśli miara kąta 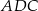 jest równa
jest równa  , to
, to
A) 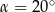 B)
B) 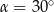 C)
C) 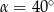 D)
D) 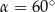
Dany jest równoramienny trójkąt 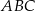 o kącie przy podstawie
o kącie przy podstawie 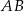 równym
równym 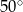 . Punkt
. Punkt 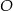 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 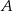 i
i 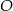 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 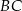 w punkcie
w punkcie 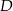 . Jeśli miara kąta
. Jeśli miara kąta 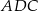 jest równa
jest równa  , to
, to
A) 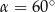 B)
B) 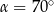 C)
C) 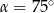 D)
D) 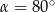
Dany jest równoramienny trójkąt 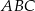 o kącie przy podstawie
o kącie przy podstawie 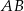 równym
równym 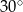 . Punkt
. Punkt 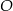 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 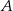 i
i 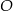 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 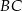 w punkcie
w punkcie 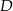 . Jeśli miara kąta
. Jeśli miara kąta 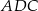 jest równa
jest równa  , to
, to
A) 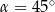 B)
B) 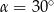 C)
C) 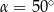 D)
D) 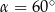
Odcinek 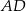 jest dwusieczną w trójkącie równoramiennym
jest dwusieczną w trójkącie równoramiennym 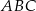 poprowadzoną do ramienia
poprowadzoną do ramienia 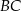 .
.
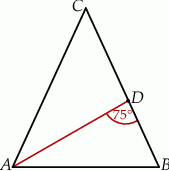
Jeżeli 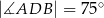 to miara kąta przy wierzchołku
to miara kąta przy wierzchołku 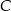 jest równa
jest równa
A) 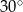 B)
B) 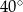 C)
C) 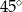 D)
D) 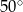
W trójkącie równoramiennym 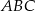 dane są
dane są 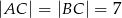 oraz
oraz 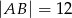 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 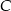 jest równa
jest równa
A) 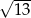 B)
B) 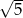 C) 1 D) 5
C) 1 D) 5
W trójkącie równoramiennym 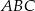 dane są
dane są 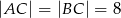 oraz
oraz 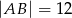 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 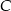 jest równa
jest równa
A) 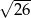 B)
B) 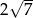 C) 2 D)
C) 2 D) 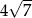
W trójkącie równoramiennym 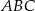 dane są
dane są 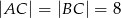 oraz
oraz 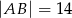 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 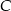 jest równa
jest równa
A) 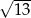 B)
B) 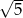 C)
C) 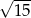 D)
D) 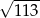
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 7. Wysokość opuszczona na podstawę ma długość
A) 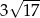 B)
B) 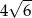 C)
C) 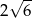 D)
D) 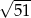
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 13. Wysokość opuszczona na podstawę ma długość
A) 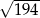 B)
B) 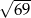 C) 12 D) 11
C) 12 D) 11
Podstawa trójkąta równoramiennego ma długość 6, a ramię ma długość 5. Wysokość opuszczona na podstawę ma długość
A) 3 B) 4 C) 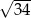 D)
D) 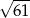
W trójkącie równoramiennym 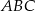 dane są
dane są 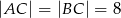 oraz
oraz 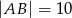 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 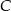 jest równa
jest równa
A) 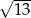 B)
B) 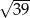 C) 6 D)
C) 6 D) 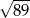
W trójkącie równoramiennym miara kąta przy podstawie jest równa 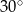 , a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
, a ramię ma długość 8 cm. Podstawa tego trójkąta ma długość
A) 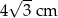 B) 4 cm C)
B) 4 cm C) 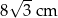 D)
D) 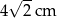
Ramię trójkąta równoramiennego ma długość 12 i tworzy z podstawą kąt o mierze 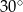 . Obwód tego trójkąta jest równy:
. Obwód tego trójkąta jest równy:
A) 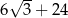 B) 30 C) 36 D)
B) 30 C) 36 D) 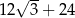
Dany jest trójkąt równoramienny 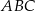 , w którym
, w którym 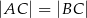 . Na podstawie
. Na podstawie 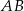 tego trójkąta leży punkt
tego trójkąta leży punkt 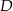 , taki że
, taki że 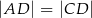 ,
, 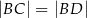 (zobacz rysunek).
(zobacz rysunek).
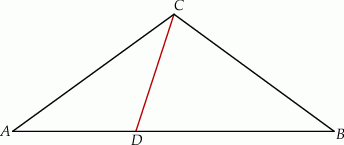
Wynika stąd, że kąt 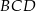 ma miarę
ma miarę
A) 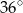 B)
B) 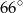 C)
C) 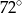 D)
D) 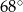
W trójkącie równoramiennym ramię ma długość 5, a kąt ostry przy podstawie jest równy  . Wysokość poprowadzona na podstawę trójkąta wynosi
. Wysokość poprowadzona na podstawę trójkąta wynosi
A) 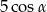 B)
B) 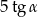 C)
C) 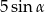 D)
D) 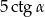
Kąt między ramionami trójkąta równoramiennego ma miarę 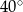 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 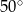 B)
B) 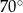 C)
C) 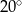 D)
D) 
Dany jest trójkąt 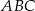 , w którym
, w którym 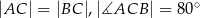 , zaś
, zaś 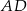 jest wysokością trójkąta. Wówczas miara kąta
jest wysokością trójkąta. Wówczas miara kąta 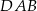 wynosi
wynosi
A) 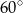 B)
B) 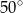 C)
C) 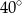 D)
D) 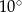
Kąt między ramionami trójkąta równoramiennego ma miarę 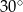 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 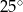 B)
B) 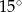 C)
C) 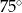 D)
D) 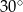
Kąt między ramionami trójkąta równoramiennego wynosi 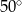 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 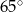 B)
B) 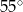 C)
C) 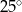 D)
D) 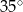
Kąt między ramionami trójkąta równoramiennego ma miarę 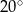 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 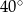 B)
B) 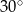 C)
C) 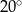 D)
D) 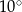
Kąt między ramionami trójkąta równoramiennego wynosi 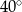 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 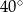 B)
B) 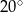 C)
C) 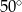 D)
D) 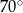
W trójkącie równoramiennym 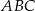 o podstawie
o podstawie 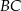 dane są:
dane są: 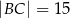 oraz
oraz 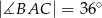 . Odcinek
. Odcinek 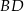 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta 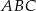 (zobacz rysunek).
(zobacz rysunek).
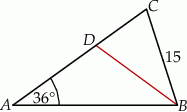
Wówczas długość odcinka 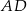 jest równa
jest równa
A) 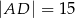 B)
B) 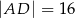 C)
C) 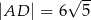 D)
D) 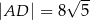
Z odcinków o długościach: 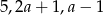 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że
A) 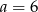 B)
B) 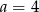 C)
C) 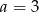 D)
D) 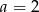
Z odcinków o długościach: 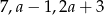 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że
A) 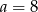 B)
B) 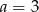 C)
C) 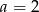 D)
D) 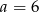
W pewnym trójkącie równoramiennym największy kąt ma miarę 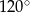 , a najdłuższy bok ma długość 12 (zobacz rysunek).
, a najdłuższy bok ma długość 12 (zobacz rysunek).
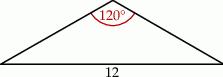
Najkrótsza wysokość tego trójkąta ma długość równą
A) 6 B) 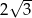 C)
C) 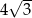 D)
D) 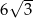
W pewnym trójkącie równoramiennym największy kąt ma miarę 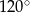 , a ramię ma długość 6 (zobacz rysunek).
, a ramię ma długość 6 (zobacz rysunek).

Najkrótsza wysokość tego trójkąta ma długość równą
A) 4 B) 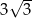 C)
C) 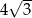 D) 3
D) 3
Ile wynosi tangens kąta  zaznaczonego na rysunku poniżej?
zaznaczonego na rysunku poniżej?
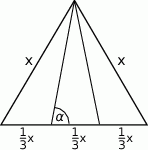
A) 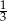 B)
B) 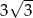 C)
C) 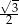 D)
D) 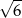
W trójkącie równoramiennym 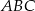 poprowadzono wysokość
poprowadzono wysokość 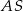 , która utworzyła z podstawą kąt o mierze
, która utworzyła z podstawą kąt o mierze 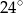 (zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości
(zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości 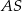 jest liczbą z przedziału
jest liczbą z przedziału
A) 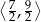 B)
B) 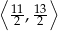 C)
C) 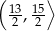 D)
D) 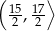
Dany jest trójkąt równoramienny 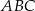 , w którym
, w którym 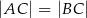 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka 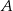 przecina bok
przecina bok 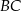 tego trójkąta w punkcie
tego trójkąta w punkcie 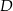 . Kąt
. Kąt 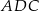 ma miarę
ma miarę 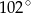 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę
A) 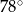 B)
B) 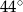 C)
C) 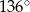 D)
D) 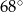
Punkt 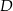 jest środkiem podstawy trójkąta równoramiennego
jest środkiem podstawy trójkąta równoramiennego 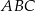 , w którym
, w którym 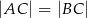 . Odległość punktu
. Odległość punktu 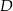 od prostej
od prostej 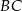 jest równa 12, a długość odcinka
jest równa 12, a długość odcinka 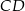 jest równa 20.
jest równa 20.
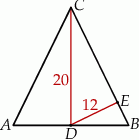
Podstawa 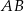 trójkąta
trójkąta 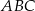 ma długość
ma długość
A) 15 B) 30 C) 24 D) 16
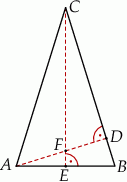
Wysokości 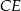 i
i 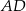 trójkąta równoramiennego
trójkąta równoramiennego 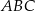 przecinają się w punkcie
przecinają się w punkcie 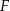 . Podstawa trójkąta
. Podstawa trójkąta 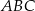 ma długość 13, a jego obwód jest równy 65.
ma długość 13, a jego obwód jest równy 65.
Stosunek pola trójkąta 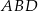 do pola trójkąta
do pola trójkąta 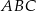 jest równy
jest równy
A)  B)
B) 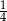 C)
C) 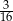 D)
D) 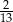
W trójkącie równoramiennym 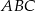 wysokość ma długość 8, a długość podstawy
wysokość ma długość 8, a długość podstawy 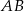 stanowi
stanowi 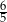 długości ramienia. Podstawa tego trójkąta ma długość
długości ramienia. Podstawa tego trójkąta ma długość
A) 30 B) 6 C) 12 D) 10
Podstawa trójkąta równoramiennego 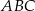 ma długość 19. Na ramionach
ma długość 19. Na ramionach 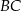 i
i 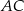 wybrano punkty
wybrano punkty 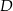 i
i 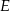 odpowiednio tak, że
odpowiednio tak, że 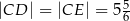 oraz
oraz 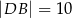 .
.
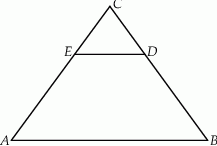
Odległość między prostymi 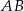 i
i 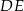 jest równa
jest równa
A) 5 B) 8 C) 10 D) 12
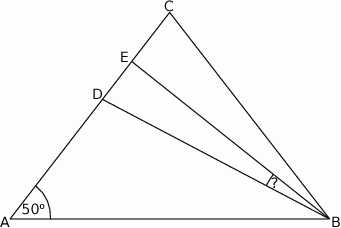
W trójkącie równoramiennym 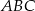 spełnione są warunki:
spełnione są warunki: 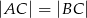 ,
, 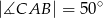 . Odcinek
. Odcinek 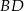 jest dwusieczną kąta
jest dwusieczną kąta 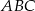 , a odcinek
, a odcinek 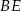 jest wysokością opuszczoną z wierzchołka
jest wysokością opuszczoną z wierzchołka 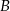 na bok
na bok 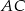 . Miara kąta
. Miara kąta 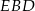 jest równa
jest równa
A) 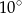 B)
B) 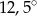 C)
C) 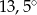 D)
D)